Exam 5: Linear Inequalities and Linear Programming

Use graphical methods to solve the linear programming problem. -Maximize z = 6x + 7y subject to: 2x + 3y ≤ 12 2x + y ≤ 8 x ≥ 0 Y ≥ 0

Solve the problem. -A salesperson has two job offers.Company A offers a weekly salary of $180 plus commission of 6% of sales. Company B offers a weekly salary of $360 plus commission of 3% of sales.What is the amount of sales above Which Company A's offer is the better of the two?

Provide an appropriate response. -Solve the following linear programming problem by determining the feasible region on the graph below and testing the corner points: Minimize C = x₁ + 6x₂ subject to 3x₁ + 4x₂ ≥ 36 2x₁ + x₂ ≤ 14 x₁, x₂ ≥ 0 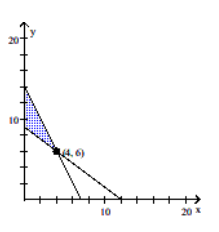x₁ is shown on the x-axis and x₂ on the y-axis.

Graph the solution set of the system of linear inequalities and indicate whether the solution region is bounded or unbounded. -y ≤ -2x + 2 y ≥ x - 7

Use graphical methods to solve the linear programming problem. -Minimize z = 2x + 4y subject to: x + 2y ≥ 10 3x + y ≥ 10 x ≥ 0 Y ≥ 0

Provide an appropriate response. -Find the coordinates of the corner points of the solution region for: 3x + 2y ≥ 54 4x + 5y ≤ 100 x ≥ 0 y ≥ 0

Define the variable(s) and translate the sentence into an inequality. -Sales of wheat bread are at least $2000 greater than sales of white bread.

Use graphical methods to solve the linear programming problem. -Minimize z = 4x + 5y subject to: 2x - 4y ≤ 10 2x + y ≥ 15 x ≥ 0 Y ≥ 0

Suppose an horse feed to be mixed from soybean meal and oats must contain at least 200 lb of protein and 40 lb of fat.Each sack of soybean meal costs $20 and contains 60 lb of protein and 10 lb of fat.Each sack of oats costs $10 and contains 20 lb of protein and 5 lb of fat.How many sacks of each should be used to satisfy the minimum requirements at minimum cost?

Solve the problem. -Formulate the following problem as a linear programming problem (DO NOT SOLVE):A steel company produces two types of machine dies,part A and part B.Part A requires 6 hours of casting time and 4 hours of firing time.Part B requires 8 hours of casting time and 3 hours of firing time.The maximum number of hours per week available for casting and firing are 85 and 70,respectively.The company makes a $2.00 profit on each part A that it produces,and a $6.00 profit on each part B that it produces.How many of each type should the company produce each week in order to maximize its profit? (Let x1 equal the number of A parts and x2 equal the number of B parts produced each week.)

Use graphical methods to solve the linear programming problem. -A math camp wants to hire counselors and aides to fill its staffing needs at minimum cost.The average monthly salary of a counselor is $2400 and the average monthly salary of an aide is $1100.The camp can accommodate up to 45 staff members and needs at least 30 to run properly.They must have at least 10 aides,and may have up to 3 aides for every 2 counselors.How many counselors and how many aides should the camp hire to minimize cost?

Define the variable(s) and translate the sentence into an inequality. -Enrollment is below 8000 students.

The Southern States Ring Company designs and sells two types of rings: the brass and the aluminum.They can produce up to 24 rings each day using up to 60 total man-hours of labor per day.It takes 3 man-hours to make one brass ring and 2 man-hours to make one aluminum ring.How many of each type of ring should be made daily to maximize the company's profit,if the profit on a brass ring is $40 and on an aluminum ring is $35?

Provide an appropriate response. -The corner points for the bounded feasible region determined by the system of inequalities: 2x₁ + 5x₂ ≤ 20 x₁ + x₂ ≤ 7 x₁,x₂ ≥ 0 are O = (0,0),A = (0,4),B = (5,2)and C = (7,0).Find the optimal solution for the objective profit function: P(x)= 3x₁ + 7x₂

Solve the problem. -Company A rents copiers for a monthly charge of $300 plus 10 cents per copy.Company B rents copiers for a monthly charge of $600 plus 5 cents per copy.What is the number of copies above which Company A's charges are the higher of the two?

Graph the constant-profit lines through (3, 2) and (5, 3). Use a straightedge to identify the corner point(s) where the maximum profit occurs for the given objective function. 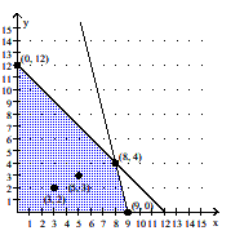-P = 5x + y

Provide an appropriate response. -The corner points for the bounded feasible region determined by the system of inequalities: 5x₁ + 2x₂ ≤ 40 x₁ + 3x₂ ≤ 21 x₁,x₂ ≥ 0 are O = (0,0),A = (0,7),B = (6,5)and C = (8,0).Find the optimal solution for the objective profit function: P = 5x₁ + 5x₂

Use graphical methods to solve the linear programming problem. -The Old-World Class Ring Company designs and sells two types of rings: the BRASS and the GOLD.They can produce up to 24 rings each day using up to 60 total man-hours of labor.It takes 3 man-hours to make one BRASS ring and 2 man-hours to make one GOLD ring.How many of each type of ring should be made daily to maximize the company's profit,if the profit on a BRASS ring is $40 and on an GOLD ring is $30?

Solve the problem. -A vineyard produces two special wines a white,and a red.A bottle of the white wine requires 14 pounds of grapes and 1 hour of processing time.A bottle of red wine requires 25 pounds of grapes and 2 hours of processing time.The vineyard has on hand 2,198 pounds of grapes and can allot 160 hours of processing time to the production of these wines.A bottle of the white wine sells for $11.00,while a bottle of the red wine sells for $20.00.How many bottles of each type should the vineyard produce in order to maximize gross sales? (Solve using the geometric method.)

Provide an appropriate response. -Using a graphing calculator as needed,maximize P = 524x₁ + 479x₂ subject to 265x1 + 320x₂ ≤ 3,390 350x₁ + 345x₂ ≤ 3,795 400x₁ + 316x₂ ≤ 4,140 x1,x2 ≥ 0 Give the answer to two decimal places.