Exam 3: Differentiation
Exam 1: Preliminaries209 Questions
Exam 2: Functions, Limits and the Derivative271 Questions
Exam 3: Differentiation331 Questions
Exam 4: Applications of the Derivative183 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration313 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables205 Questions
Select questions type
The demand equation for the Sicard wristwatch is given by 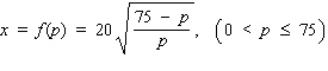 , where x (measured in units of a thousand) is the quantity demanded each week and p is the unit price in dollars.Find the rate of change of the quantity demanded of the wristwatches with respect to the unit price when the unit price is $60.Round your answer to the nearest whole number.
, where x (measured in units of a thousand) is the quantity demanded each week and p is the unit price in dollars.Find the rate of change of the quantity demanded of the wristwatches with respect to the unit price when the unit price is $60.Round your answer to the nearest whole number.
Free
(Multiple Choice)
4.9/5  (27)
(27)
Correct Answer:
D
Find the third derivative of the function. 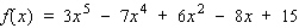
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
E
The demand equation for the Sicard wristwatch is given by 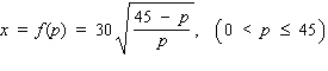 where x (measured in units of a thousand) is the quantity demanded each week and p is the unit price in dollars.Find the rate of change of the quantity demanded of the wristwatches with respect to the unit price when the unit price is $35.Round your answer to the nearest whole number.
__________ wristwatches/(dollar price increase)
where x (measured in units of a thousand) is the quantity demanded each week and p is the unit price in dollars.Find the rate of change of the quantity demanded of the wristwatches with respect to the unit price when the unit price is $35.Round your answer to the nearest whole number.
__________ wristwatches/(dollar price increase)
Free
(Short Answer)
4.8/5  (37)
(37)
Correct Answer:
-1,031
The demand function for a certain brand of compact disc is 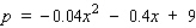 , where p is the wholesale unit price in dollars and x is the quantity demanded each week, measured in units of a thousand.
Compute the elasticity of demand (to the nearest hundredth) when x = 10.
__________
Determine whether the demand is inelastic, unitary, or elastic when x = 10.
__________
, where p is the wholesale unit price in dollars and x is the quantity demanded each week, measured in units of a thousand.
Compute the elasticity of demand (to the nearest hundredth) when x = 10.
__________
Determine whether the demand is inelastic, unitary, or elastic when x = 10.
__________
(Essay)
4.9/5  (31)
(31)
The weekly total cost function associated with manufacturing the Pulsar 25 color console television is given by 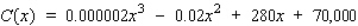 . What is the marginal average cost function
. What is the marginal average cost function 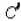 ?
?
(Multiple Choice)
4.8/5  (32)
(32)
Suppose f and g are functions that are differentiable at 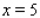 and that
and that 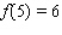 ,
, 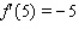 ,
, 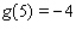 , and
, and 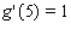 .Find the value of
.Find the value of 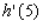 .
. 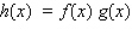
(Essay)
4.8/5  (29)
(29)
Use a differential to approximate the quantity to the nearest thousandth. 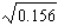
(Multiple Choice)
4.8/5  (35)
(35)
Research done in the 1930s by the French physiologist Jean Poiseuille showed that the resistance R of a blood vessel of length l and radius r is 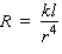 where k is a constant.Suppose a dose of the drug TPA increases r by 22%.How will this affect the resistance R? Assume that l is constant.
where k is a constant.Suppose a dose of the drug TPA increases r by 22%.How will this affect the resistance R? Assume that l is constant.
(Multiple Choice)
4.9/5  (41)
(41)
Suppose f and g are functions that are differentiable at 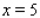 and that
and that 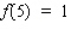 ,
, 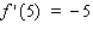 ,
, 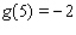 , and
, and 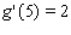 .Find the value of
.Find the value of 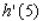 .
. 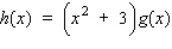
(Multiple Choice)
4.9/5  (40)
(40)
Find the slope m and an equation of the tangent line to the graph of the function f at the point 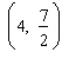 .
. 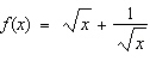
(Multiple Choice)
4.8/5  (32)
(32)
The supply equation for a certain brand of radio is given by 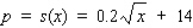 , where x is the quantity supplied and p is the unit price in dollars.Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
$__________
, where x is the quantity supplied and p is the unit price in dollars.Use differentials to approximate the change in price when the quantity supplied is increased from 10,000 units to 10,500 units.
$__________
(Short Answer)
4.8/5  (35)
(35)
The percent of mothers who work outside the home and have children younger than age 6 yr is approximated by the function 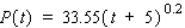 where t is measured in years, with t = 0 corresponding to the beginning of 1980. Compute
where t is measured in years, with t = 0 corresponding to the beginning of 1980. Compute 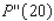 .
.
(Multiple Choice)
4.9/5  (29)
(29)
A hemisphere-shaped dome of radius 30 ft is to be coated with a layer of rust-proofer before painting.Use differentials to estimate the amount of rust-proofer needed if the coat is to be 0.05 in.thick. Hint: The volume of a hemisphere of radius r is 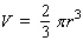 .
.
(Multiple Choice)
4.8/5  (37)
(37)
Showing 1 - 20 of 331
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)