Exam 4: Exponential Functions
Exam 1: Functions99 Questions
Exam 2: Graphical and Tabular Analysi99 Questions
Exam 3: Straight Lines and Linear Functions100 Questions
Exam 4: Exponential Functions100 Questions
Select questions type
The formula for an exponential function is Then the decay factor is:
(Multiple Choice)
4.8/5  (31)
(31)
The formula for an exponential function is . Then the decay factor is:
(Multiple Choice)
4.7/5  (31)
(31)
The size N , in thousands, of a certain animal population after 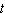 years is given in the table below. By what percentage can the population be expected to grow over any 6-year period?
years is given in the table below. By what percentage can the population be expected to grow over any 6-year period? 
(Multiple Choice)
4.9/5  (38)
(38)
The decay factor of an exponential function is 0.68. The initial value is 1.45. Then a formula for P is
(Multiple Choice)
4.9/5  (35)
(35)
The decay factor of an exponential function is 0.43. The initial value is 1.24. Then a formula for P is
(Multiple Choice)
4.8/5  (42)
(42)
The decay factor of an exponential function is 0.61. The initial value is 1.48. Then a formula for P is
(Multiple Choice)
4.9/5  (37)
(37)
The size N , in thousands, of a certain animal population after 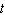 years is given in the table below. Use exponential regression to model the population size as a function of time.
years is given in the table below. Use exponential regression to model the population size as a function of time. 
(Multiple Choice)
4.8/5  (41)
(41)
The monthly percentage decay rate for a certain exponential function is 8%. By what per- centage does the function decay in a week? (Assume there are four weeks in a month.)
(Multiple Choice)
4.8/5  (42)
(42)
Use exponential regression to determine what happens to when 1 is added to t. 
(Multiple Choice)
4.9/5  (34)
(34)
The magnitude M of an earthquake depends on the relative intensity I of the quake. The relationship is
Express the relative intensity as a function of the magnitude.
(Multiple Choice)
4.8/5  (39)
(39)
Use exponential regression to determine what happens to when 1 is added to t. 
(Multiple Choice)
4.8/5  (34)
(34)
The magnitude of earthquake 1 is 3.7, and the magnitude of earthquake 2 is 5.6. How do their intensities compare?
(Multiple Choice)
5.0/5  (38)
(38)
The magnitude M of an earthquake depends on the relative intensity I of the quake. The relationship is Express the relative intensity as a function of the magnitude.
(Multiple Choice)
4.7/5  (36)
(36)
A function shows constant percentage growth. Which of the following may be the graph of this function?
(Multiple Choice)
4.8/5  (36)
(36)
Use exponential regression to determine what happens to when 1 is added to t. 
(Multiple Choice)
4.9/5  (37)
(37)
The size N , in thousands, of a certain animal population after 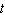 years is given in the table below. Use exponential regression to model the population size as a function of time.
years is given in the table below. Use exponential regression to model the population size as a function of time. 
(Multiple Choice)
4.9/5  (25)
(25)
Showing 41 - 60 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)