Exam 3: Arithmetic for Computers

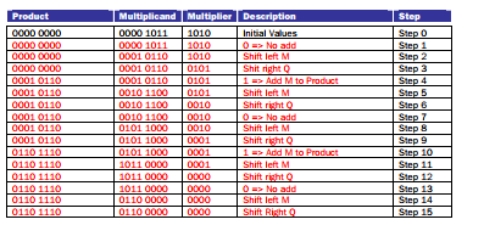
This problem covers 4-bit binary multiplication. Fill in the table for the Product, Multplier and Multiplicand for each step. You need to provide the DESCRIPTION of the step being performed (shift left, shift right, add, no add). The value of M (Multiplicand) is 1011, Q (Multiplier) is initially 1010.

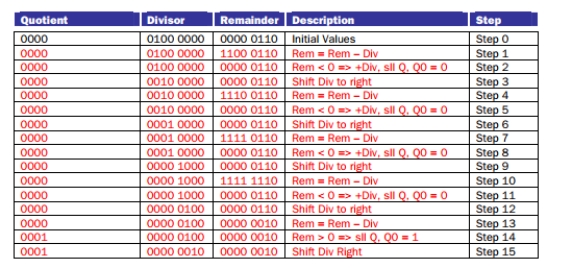
This problem covers 4-bit binary unsigned division (similar to Fig. 3.11 in the text). Fill in the table for the Quotient, Divisor and Dividend for each step. You need to provide the DESCRIPTION of the step being performed (shift left, shift right, sub). The value of Divisor is 4 (0100, with additional 0000 bits shown for right shift), Dividend is 6 (initially loaded into the Remainder).

What is the smallest positive (not including +0) representable number in 32-bit IEEE 754 single precision floating point? Show the bit encoding and the value in base 10 (fraction or decimal OK).

This problem covers floating-point IEEE format. (a) List four floating-point operations that cause NaN to be created? (b) Assuming single precision IEEE 754 format, what decimal number is represent by this word: 1 01111101 00100000000000000000000 (Hint: remember to use the biased form of the exponent.)

Why is the 2's complement representation used most often? Give an example of overflow when: (a) 2 positive numbers are added (b) 2 negative numbers are added (c) A-B where B is a negative number

Perform the following operations by converting the operands to 2's complement binary numbers and then doing the addition or subtraction shown. Please show all work in binary, operating on 16-bit numbers. (a) 3 + 12 (b) 13 - 2 (c) 5 - 6 (d) -7 - (-7)

The floating-point format to be used in this problem is a normalized format with 1 sign bit, 3 exponent bits, and 4 mantissa bits. The exponent field employs an excess-4 coding. The bit fields in a number are (sign, exponent, mantissa). Assume that we use unbiased rounding to the nearest even specified in the IEEE floating point standard. (a) Encode the following numbers in the above format: (b) (1) 1.0binary (c) (2) 0.0011011binary (b) In one sentence for each, state the purpose of guard, rounding, and sticky bits for floating point arithmetic. (c) Perform rounding on the following fractional binary numbers, use the bit positions in italics to determine rounding (use the rightmost 3 bits): (1) Round to positive infinity: +0.100101110binary (2) Round to negative infinity: -0.001111001binary (4) Unbiased to the nearest even: +0.100101100binary (5) Unbiased to the nearest even: -0.100100110binary (d) What is the result of the square root of a negative number?

The floating-point format to be used in this problem is an 8-bit IEEE 754 normalized format with 1 sign bit, 4 exponent bits, and 3 mantissa bits. It is identical to the 32-bit and 64-bit formats in terms of the meaning of fields and special encodings. The exponent field employs an excess- 7coding. The bit fields in a number are (sign, exponent, mantissa). Assume that we use unbiased rounding to the nearest even specified in the IEEE floating point standard. (a) Encode the following numbers the 8-bit IEEE format: (b) Perform the computation 1.011binary + 0.0011011binary showing the correct state of the guard, round and sticky bits. There are three mantissa bits. (c) Decode the following 8-bit IEEE number into their decimal value: 1 1010 101 (d) Decide which number in the following pairs are greater in value (the numbers are in 8-bit IEEE 754 format): (1) 0 0100 100 and 0 0100 111 (2) 0 1100 100 and 1 1100 101 (e) In the 32-bit IEEE format, what is the encoding for negative zero? (f) In the 32-bit IEEE format, what is the encoding for positive infinity? (1) 0.0011011binary (2) 16.0decimal

Prove that Sign Magnitude and One's Complement addition cannot be performed correctly by a single unsigned adder. Prove that a single n-bit unsigned adder performs addition correctly for all pairs of n-bit Two's Complement numbers for n=2. You should ignore overflow concerns and the n+1 carry bit. (For an optional added challenge, prove for n=2 by first proving for all n.)

Consider 2's complement 4-bit signed integer addition and subtraction. (a) Since the operands can be negative or positive and the operator can be subtraction or addition, there are 8 possible combinations of inputs. For example, a positive number could be added to a negative number, or a negative number could be subtracted from a negative number, etc. For each of them, describe how the overflow can be computed from the sign of the input operands and the carry out and sign of the output. Fill in the table below: 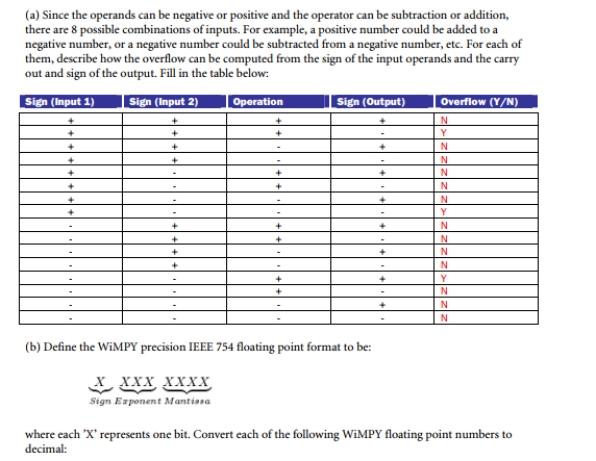(a) 00000000 (b) 11011010 (c) 01110000

We're going to look at some ways in which binary arithmetic can be unexpectedly useful. For this problem, all numbers will be 8-bit, signed, and in 2's complement. (a) For x = 8, compute x & (−x). (& here refers to bitwise-and, and − refers to arithmetic negation.) (b) For x = 36, compute x & (−x). (c) Explain what the operation x & (−x) does. (d) In some architectures (such as the PowerPC), there is an instruction adde rX=rY,rZ, which performs the following: rX = rY + rZ + CA where CA is the carry flag. There is also a negation instruction, neg rX=rY which performs: rX = 0 - rY Both adde and neg set the carry flag. gcc (the GNU C Compiler) will often use these instructions in the following sequence in order to implement a feature of the C language: neg r1=r0 adde r2=r1,r0 Explain, simply, what the relationship between r0 and r2 is (Hint: r2 has exactly two possible values), and what C operation it corresponds to. Be sure to show your reasoning.

Using 32-bit IEEE 754 single precision floating point with one(1) sign bit, eight (8) exponent bits and twenty three (23) mantissa bits, show the representation of -11/16 (-0.6875).