Exam 6: Rational Expression and Equations
Exam 1: A Review of Basic Algebra312 Questions
Exam 2: Graphs, Equations of Lines, and Functions286 Questions
Exam 3: Systems of Equations280 Questions
Exam 4: Inequalities193 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions299 Questions
Exam 6: Rational Expression and Equations297 Questions
Exam 7: Radical Expressions and Equations324 Questions
Exam 8: Quadratic Equations, Functions, and Inequalities132 Questions
Exam 9: Exponential and Logarithmic Functions259 Questions
Exam 10: Conic Sections; More Graphing122 Questions
Exam 11: Miscellaneous Topics102 Questions
Select questions type
To quickly find the sum of a list of fractions, such as mathematicians use the formula Solve the formula for b .
Free
(Essay)
4.9/5  (26)
(26)
Correct Answer:
a. What numbers cannot be solutions of the equation ?
b. Solve:
Free
(Essay)
4.7/5  (37)
(37)
Correct Answer:
a. ,
b.
Perform the operations and simplify the result when possible.
Free
(Essay)
4.9/5  (35)
(35)
Correct Answer:
A recipe for guacamole dip calls for 7 avocados. If they are advertised at 3 for $1.86, what will 7 avocados cost?
$ __________
(Short Answer)
4.9/5  (31)
(31)
Express the verbal model in symbols. C varies jointly with v , z , and x .
(Multiple Choice)
4.9/5  (45)
(45)
A man roller-blades at a rate 6 miles per hour faster than he jogs. In the same time it takes him to roller-blade 6 miles he can jog 2 miles. How fast does he jog?
(Short Answer)
4.7/5  (38)
(38)
Perform the operations and simplify the result when possible.
(Multiple Choice)
4.8/5  (40)
(40)
Find 35 by using synthetic division to evaluate the polynomial
(Short Answer)
4.8/5  (27)
(27)
If P ( x ) is a polynomial and if , then k is called a __________ of the polynomial.
(Multiple Choice)
4.9/5  (38)
(38)
A boat that travels 19 mph in still water can travel 24 miles downstream in the same time as it takes to travel 14 miles upstream. Find the speed of the current in the river. 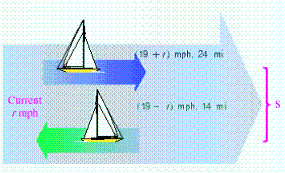 __________ mph
__________ mph
(Short Answer)
4.7/5  (27)
(27)
Use the remainder theorem and synthetic division to find P ( k ). __________
(Short Answer)
4.9/5  (33)
(33)
Showing 1 - 20 of 297
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)