Exam 5: Differentiation
Exam 1: Prerequisites7 Questions
Exam 2: Functions and Their Graphs49 Questions
Exam 3: Polynomial and Rational Functions84 Questions
Exam 4: Limits and Their Properties51 Questions
Exam 5: Differentiation77 Questions
Exam 6: Applications of Differentiation107 Questions
Exam 7: Integration64 Questions
Exam 8: Exponential and Logarithmic Functions48 Questions
Exam 9: Exponential and Logarithmic Functions and Calculus54 Questions
Exam 10: Trigonometric Functions79 Questions
Exam 11: Analytic Trigonometry73 Questions
Exam 12: Trigonometric Functions and Calculus25 Questions
Exam 13: Topics in Analytic Geometry60 Questions
Exam 14: Additional Topics in Trigonometry86 Questions
Select questions type
Find an equation of the tangent line to the graph of the function 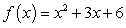 at the point
at the point 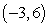 .
.
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
B
Suppose that an automobile's velocity starting from rest is 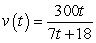 where v is measured in feet per second. Find the acceleration at 9 seconds. Round your answer to one decimal place.
where v is measured in feet per second. Find the acceleration at 9 seconds. Round your answer to one decimal place.
Free
(Multiple Choice)
4.7/5  (43)
(43)
Correct Answer:
D
Find the second derivative of the function 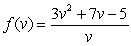 .
.
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
B
Suppose the position function for a free-falling object on a certain planet is given by 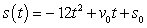 . A silver coin is dropped from the top of a building that is 1374 feet tall. Find velocity of the coin at impact. Round your answer to the three decimal places.
. A silver coin is dropped from the top of a building that is 1374 feet tall. Find velocity of the coin at impact. Round your answer to the three decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
A conical tank (with vertex down) is 20 feet across the top and 26 feet deep. If water is flowing into the tank at a rate of 16 cubic feet per minute, find the rate of change of the depth of the water when the water is 12 feet deep.
(Multiple Choice)
4.7/5  (42)
(42)
The graph of the function f is given below. Select the graph of 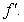
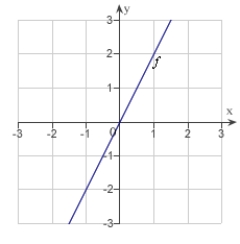
(Multiple Choice)
4.9/5  (35)
(35)
Use the alternative form of the derivative to find the derivative of the function 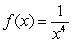 at
at 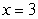 .
.
(Multiple Choice)
4.8/5  (39)
(39)
Suppose the position function for a free-falling object on a certain planet is given by is given by 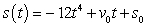 . A silver coin is dropped from the top of a building that is 1366 feet tall. Determine the velocity function for the coin.
. A silver coin is dropped from the top of a building that is 1366 feet tall. Determine the velocity function for the coin.
(Multiple Choice)
4.8/5  (42)
(42)
Suppose the position function for a free-falling object on a certain planet is given by 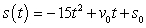 . A silver coin is dropped from the top of a building that is 1362 feet tall. Find the instantaneous velocity of the coin when
. A silver coin is dropped from the top of a building that is 1362 feet tall. Find the instantaneous velocity of the coin when 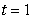 .
.
(Multiple Choice)
4.9/5  (35)
(35)
Find an equation of the tangent line to the graph of the function 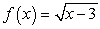 at the point
at the point 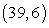 .
.
(Multiple Choice)
4.8/5  (29)
(29)
Differentiate 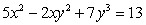 with respect to t (x and y are functions of t).
with respect to t (x and y are functions of t).
(Multiple Choice)
4.8/5  (38)
(38)
Use the rules of differentiation to find the derivative of the function 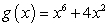 .
.
(Multiple Choice)
4.8/5  (29)
(29)
Find the slope m of the line tangent to the graph of the function 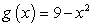 at the point
at the point 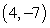 .
.
(Multiple Choice)
4.8/5  (40)
(40)
A projectile is shot upwards from the surface of the earth with an initial velocity of 148 meters per second. The position function is 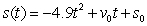 .What is its velocity after 4 seconds?
.What is its velocity after 4 seconds?
(Multiple Choice)
4.9/5  (34)
(34)
Find the derivative of the following function using the limiting process. 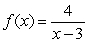
(Multiple Choice)
4.9/5  (35)
(35)
The radius r of a sphere is increasing at a rate of 2 inches per minute. Find the rate of change of the volume when r = 9 inches.
(Multiple Choice)
4.9/5  (29)
(29)
Showing 1 - 20 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)