Exam 4: Solving Systems of Equations and Inequalities
Exam 1: An Introduction to Algebra114 Questions
Exam 2: Equations, Inequalities, and Problem Solving92 Questions
Exam 3: Graphs, Linear Equations, and Inequalities in Two Variables; Functions From Campus to Careers: Physical Therapis101 Questions
Exam 4: Solving Systems of Equations and Inequalities60 Questions
Exam 5: Exponents and Polynomials98 Questions
Exam 6: Factoring and Quadratic Equations62 Questions
Exam 7: Rational Expressions and Equations75 Questions
Exam 8: Roots and Radicals98 Questions
Exam 9: Quadratic Equations53 Questions
Select questions type
A merchant wishes to mix peanuts that sell for $2.5 per pound and cashews that sell for $8 per pound to get 100 pounds of mixed nuts that sell for $4.50 per pound. Let x equal the number of pounds of peanuts and y equal the number of pounds of cashews. If solving this by writing two equations in two variables, which of the following could be one of the equations?
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
Use the dimensions in the illustration to find w , the width of the river. The two triangles in the illustration are similar. 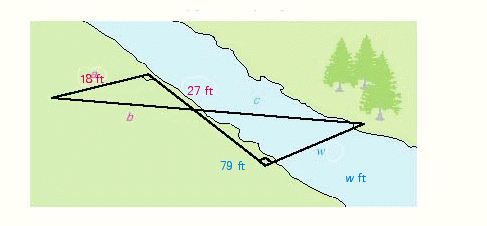
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
A
Solve the system by using either the substitution method or the elimination-by-addition method, whichever seems more appropriate.
(Multiple Choice)
4.8/5  (29)
(29)
Use two equations in two variables to solve the following problem. Two pairs of shoes and four pairs of socks cost $107, and three pairs of shoes and five pairs of socks cost $156. Find the cost of a pair of socks.
(Multiple Choice)
4.8/5  (38)
(38)
In solving a system of equations by the elimination method, the result 1 = 1 is obtained. Which of the following statements is true?
(Multiple Choice)
4.8/5  (37)
(37)
Dry Boat Works wholesales aluminum boats for $500 and fiberglass boats for $300. Northland Marina wants to order at least $750 worth but no more than $1,500 worth of boats. Write a system of linear inequalities which describes all possible combinations of aluminum boats ( x )and fiberglass boats ( y )that can be ordered, graph the system of inequalities, and determine whether the ordered pairs satisfy the inequality.
(Multiple Choice)
4.9/5  (38)
(38)
If the addition method is used to solve the following system, by what would we multiply the first equation to eliminate m ?
(Multiple Choice)
4.8/5  (32)
(32)
Use the addition method to solve the system. If the equations of the system are dependent, or if a system is inconsistent, so indicate.
(Multiple Choice)
4.8/5  (41)
(41)
Solve the system by any method, if possible. If the system is inconsistent, or if the equations are dependent, so indicate.
(Short Answer)
4.8/5  (35)
(35)
Part of $2,200 is invested at 12%, another part at 13%, and the remainder at 14%. The total yearly income from the three investments is $295. The sum of the amounts invested at 12% and 13% equals the amount invested at 14%. Determine how much is invested at each rate.
(Multiple Choice)
4.8/5  (33)
(33)
Refer to the illustration. Answer the questions. 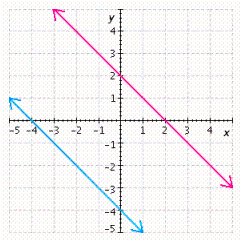 How many solutions does the system of equations have? Are the equations dependent or independent?
How many solutions does the system of equations have? Are the equations dependent or independent?
(Multiple Choice)
4.8/5  (30)
(30)
Use the method of elimination to find the y -coordinate of the solution of the following system of equations.
(Multiple Choice)
4.9/5  (45)
(45)
Use the substitution method to solve the following system. If the equations of the system are dependent, or if the system is inconsistent, so indicate.
(Multiple Choice)
4.9/5  (41)
(41)
Use two equations in two variables to solve the following problem. The salaries of the president and vice president of the United States total $490,000 a year. If the President makes $210,000 more than the Vice president, find each of their salaries.
(Multiple Choice)
4.7/5  (28)
(28)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)