Exam 1: A Review of Basic Algebra
Exam 1: A Review of Basic Algebra101 Questions
Exam 2: Graphs, Equations of Lines, and Functions86 Questions
Exam 3: Systems of Linear Equations56 Questions
Exam 4: Inequalities48 Questions
Exam 5: Polynomials, Polynomial Functions, and Equations90 Questions
Exam 6: Rational Expressions90 Questions
Exam 7: Radical Expressions and Equations89 Questions
Exam 8: Quadratic Equations and Functions; Inequalities; and Algebra, Composition, and Inverses of Functions78 Questions
Exam 9: Exponential and Logarithmic Functions72 Questions
Exam 10: Conic Sections and More Graphing57 Questions
Exam 11: Miscellaneous Topics77 Questions
Select questions type
A man uses a 11-foot bar to lift a 108-pound tire. He places a rock 2 feet from the tire to act as the fulcrum. How much force must he exert to lift the tire?
(Multiple Choice)
4.8/5  (34)
(34)
Simplify the following algebraic expression and express your answer using positive exponents only. 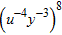
(Multiple Choice)
4.7/5  (39)
(39)
The Moon is about 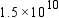 in. from Earth. Find this distance in kilometers.
in. from Earth. Find this distance in kilometers.
(Multiple Choice)
4.8/5  (41)
(41)
Which of the given graphs is the solution of the following compound inequality? x ≥ 3 and x ≤ 5
(Multiple Choice)
4.9/5  (43)
(43)
A garden store sells Kentucky bluegrass seed for $6 per pound and ryegrass seed for $3 per pound. How much rye must be mixed with 140 pounds of bluegrass to obtain a blend that will sell for $5 per pound?
(Multiple Choice)
4.9/5  (30)
(30)
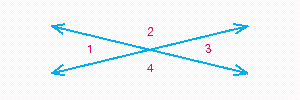
When two lines intersect as in the illustration below, four angles are formed. Angles that are side-by-side, such as 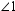 and
and 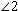 , are called adjacent angles. Angles that are nonadjacent, such as
, are called adjacent angles. Angles that are nonadjacent, such as 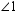 and
and 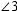 or
or 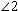 and
and 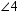 , are called vertical angles. From geometry, we know that if two lines intersect, vertical angles have the same measure. If
, are called vertical angles. From geometry, we know that if two lines intersect, vertical angles have the same measure. If 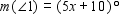 and
and 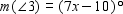 , find x . Read
, find x . Read 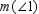 as "the measure of
as "the measure of 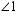 ".
". 
(Multiple Choice)
5.0/5  (38)
(38)
Paint costing $20 per gallon is to be mixed with 5 gallons of paint thinner costing $3 per gallon to make a paint that can be sold for $15 per gallon. Refer to the table below and compute how much of the new paint mixture will be produced. Paint gal Thinner gal Mixture gal
(Multiple Choice)
4.8/5  (44)
(44)
Use an equation to solve the problem. One-third of the movie audience left the theater in disgust. If 77 angry patrons walked out, how many were there originally?
(Multiple Choice)
4.7/5  (33)
(33)
An 30-pound boy wants to teeter on a 24-foot seesaw with his older sister who weighs 90 pounds. The fulcrum of the seesaw is in the center. If the boy sits at one end, how far will the boy's sister have to sit from the fulcrum to balance the seesaw?
(Multiple Choice)
4.9/5  (33)
(33)
Showing 21 - 40 of 101
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)