Exam 10: Problems With Group Decision Making

Imagine that three city council members are trying to decide how to spend a surplus. The options currently being debated are (i) spend it on improving primary education in the municipality, (ii) spend it on improving the level of medical care offered by the local hospital, or (iii) lower local taxes and use the surplus to cover the costs of existing programs. The council employs majority rule to make its decisions. The councillors have the following preference orderings over the spending choices: Councillor 1: Education $\succ$ Medical $\succ$ Tax cut Councillor 2: Medical $\succ$ Tax cut $\succ$ Education Councillor 3: Tax cut $\succ$ Education $\succ$ Medical Assume that the councillors hold a round-robin tournament that pits each alternative against every other alternative in a series of pair-wise votes. The winner is the alternative that wins the most contests. Based on this information, answer the following four questions. -Which of the outcomes, if any, is a Condorcet winner?

What is the fundamental implication of Arrow's theorem?

According to the logic of the median voter theorem, where should we expect candidates (or parties) to locate in the policy space in two-candidate (or two-party) races?

Suppose now that some polarizing event occurs that causes several voters to adopt more extreme positions on the left-right issue dimension. The new distribution of voters is shown in Figure 3. Figure 3: Illustrating the Median Voter Theorem-A Polarized Electorate 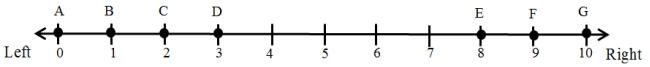-Where will parties P₁ and P₂ locate in the left-right space given the polarized nature of the electorate shown in Figure 3?

Do voters need to have single-peaked preferences in order for the Median Voter Theorem to hold?

assume that Councillor 3 has to take a family member to the emergency room and has a very poor experience with the level of medical care provided at the local hospital. This leads her to view improving medical care as a higher priority than improving education in the municipality, if money is to be spent improving any programs. Councillors 1 and 2 do not change their preference orderings. Thus, the councillors now have the following preference orderings over the spending choices: Councillor 1: Education $\succ$ Medical $\succ$ Tax cut Councillor 2: Medical $\succ$ Tax cut $\succ$ Education Councillor 3: Tax cut $\succ$ Medical $\succ$ Education Assume that the councillors hold a round-robin tournament that pits each alternative against every other alternative in a series of pair-wise votes. The winner is the alternative that wins the most contests. Based on this information, answer the following four questions. -Given the preference orderings listed above, what would the result be of a pair-wise contest between the spending choices tax cut and education?

Does Arrow's theorem apply to majority rule decision-making procedures?

Figure 1 illustrates an election in which there are seven voters (A, B, C, D, E, F, G) arrayed along a single left-right issue dimension that runs from 0 (most left) to 10 (most right). Each voter is assumed to have a single-peaked preference ordering over the issue dimension and to vote for the party that is located closest to her ideal point. The voters are participating in a majority rule election in which there are two parties, P1 and P2, competing for office. These parties can be thought of as "office-seeking" parties since they only care about winning the election and getting into office. Figure 1: Illustrating the Median Voter Theorem -Now suppose that P₁ locates at position 4 on the left-right issue dimension and that P₂ locates at position 4. Who wins the election in the situation illustrated by Figure 1?