Exam 1: Formal Languages and Automata Theory: Part A
Exam 1: Formal Languages and Automata Theory: Part A25 Questions
Exam 2: Formal Languages and Automata Theory: Part B25 Questions
Exam 3: Compiler Construction and Parsing Algorithms24 Questions
Exam 4: Compilation and Programming Languages22 Questions
Select questions type
Let SHAM3 be the problem of finding a Hamiltonian cycle in a graph G =(V,E)with V divisible by 3 and DHAM3 be the problem of determining if a Hamiltonian cycle exists in such graphs. Which one of the following is true?
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
A
S -> aSa| bSb| a| b ; The language generated by the above grammar over the alphabet {a,b} is the set of
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
B
Consider the languages: L1 ={a^n b^n c^m | n,m >01 and L2 ={a^n b^m c^m |n,m> o)
Which one of the following statements is FALSE?
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
A
Consider the languagesL1={0^{i}1^{j}|i != j},L2={0^{i}1^{j}|i = j},L3 = {0^{i}1^{j}|i = 2j+1},L4 = {0^{i}1^{j}|i != 2j}.Which one of the following statements is true?
(Multiple Choice)
4.9/5  (35)
(35)
Let L1 be a recursive language. Let L2 and L3 be languages that are recursively enumerable but not recursive. Which of the following statements is not necessarily true?
(Multiple Choice)
4.8/5  (43)
(43)
A minimum state deterministic finite automation accepting the language L = {W |W € {0,1}* , number of 0's and 1's in W are divisible by 3 and 5 respectively has
(Multiple Choice)
4.8/5  (43)
(43)
If s is a string over (0 + 1)* then let n0 (s) denote the number of 0's in s and n1 (s)the number of l's in s. Which one of the following languages is not regular?
(Multiple Choice)
4.9/5  (37)
(37)
Consider the following two problems on undirected graphs:
?: Given G(V,E), does G have an independent set of size |v|-4?
?: Given G(V,E), does G have an independent set of size 5?
Which one of the following is TRUE?
(Multiple Choice)
4.9/5  (34)
(34)
Consider the set of strings on {0,1} in which, every substring of 3 symbols has at most two zeros. For examples, 001110 and 011001 are in the language, but 100010 is not. All strings of length less than 3 are also in the language. A partially completed DFA that accepts this language is shown below. The missing arcs in the DFA are
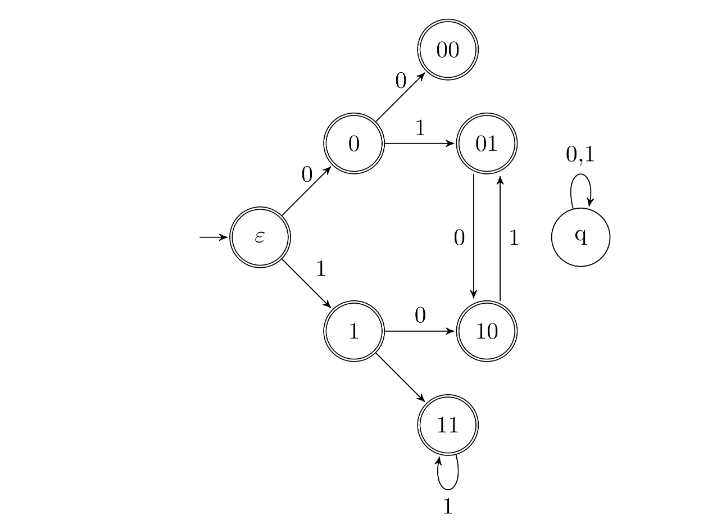
(Multiple Choice)
4.8/5  (34)
(34)
For S € (0+1)* let d(s)denote the decimal value of s(e.g.d(101)= 5).Let L = {s € (0 + 1) | d (s) mod 5 = 2 and d (s) mod 7 != 4)}Which one of the following statements is true?
(Multiple Choice)
4.8/5  (35)
(35)
Consider the language L1,L2,L3 as given below.
L1={0^{p}1^{q} | p,q \in N}
L2={0^{p}1^{q} | p,q \in N and p=q} L3={0^{p}1^{q}1^{r} | p,q,r \in N and p=q=r}
Which of the following statements is NOT TRUE?
(Multiple Choice)
4.7/5  (34)
(34)
Consider the following statements about the context free grammarG = {S - >SS, S - >ab, S - >ba, S - ?}I. G is ambiguousII. G produces all strings with equal number of a's and b'sIII. G can be accepted by a deterministic PDA.Which combination below expresses all the true statements about G?
(Multiple Choice)
4.8/5  (26)
(26)
The minimum state automaton equivalent to the above FSA has the following number of states
(Multiple Choice)
4.9/5  (42)
(42)
Let L1 be a recursive language, and let L2 be a recursively enumerable but not a recursive language. Which one of the following is TRUE?
(Multiple Choice)
4.9/5  (32)
(32)
Definition of a language L with alphabet {a} is given as following. L= { a^{nk} | k > 0, and n is a positive integer constant} What is the minimum number of states needed in a DFA to recognize L?
(Multiple Choice)
4.8/5  (36)
(36)
Let L1 be a regular language, L2 be a deterministic context-free language and L3 a recursively enumerable, but not recursive, language. Which one of the following statements is false?
(Multiple Choice)
4.8/5  (43)
(43)
Consider the regular language L =(111+11111)*. The minimum number of states
(Multiple Choice)
4.7/5  (38)
(38)
Consider the languages: GATE[2005]L1 = {wwR w €{0, 1} *1L2 ={w#ww € {O,1}*},where # is a special symbolL3 ={www € {0,1}*}Which one of the following is TRUE?
(Multiple Choice)
4.7/5  (43)
(43)
Which of the following problems are decidable?
1) Does a given program ever produce an output?
2) If L is a context-free language, then is L' (complement of L) also context-free?
3) If L is a regular language, then is L' also regular?
4) If L is a recursive language, then, is L' also recursive?
(Multiple Choice)
4.7/5  (35)
(35)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)