Exam 6: Categorical Logic: Syllogisms
Exam 1: Basic Concepts110 Questions
Exam 2: Identifying Arguments40 Questions
Exam 3: Logic and Language76 Questions
Exam 4: Informal Fallacies63 Questions
Exam 5: Categorical Logic: Statements80 Questions
Exam 6: Categorical Logic: Syllogisms110 Questions
Exam 7: Statement Logic: Truth Tables80 Questions
Exam 8: Statement Logic: Proofs60 Questions
Exam 9: Predicate Logic115 Questions
Exam 10: Inductive Logic138 Questions
Select questions type
According to modern logicians, "All elves are people with infrared vision" is equivalent to "If anything is an elf, then it is a person with infrared vision."
(True/False)
4.9/5  (33)
(33)
The only requirement when removing term complements is that the changes we make to each statement must produce a logically equivalent statement.
(True/False)
4.8/5  (47)
(47)
Aristotelian and modern logicians agree that universal categorical statements have existential import.
(True/False)
4.8/5  (27)
(27)
When removing term-complements, which of the following is not a permissible change?
(Multiple Choice)
5.0/5  (31)
(31)
The Venn diagram representation of "No sailors are pirates" is which of the following?
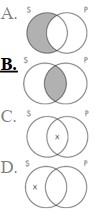
(Multiple Choice)
4.9/5  (34)
(34)
The mood of a standard-form categorical syllogism whose major premise is universal affirmative, minor premise is particular affirmative, and conclusion is particular affirmative would be
(Multiple Choice)
4.9/5  (43)
(43)
Rewrite the following argument as a standard-form categorical syllogism; then identify its mood and figure: All patriotic citizens are mindless followers of the government, and all soldiers are mindless followers of the government, so all soldiers are patriotic citizens.
(Short Answer)
4.9/5  (32)
(32)
In a standard form sorites, the subject term of the conclusion must occur in the first premise.
(True/False)
4.9/5  (40)
(40)
A categorical statement has existential import if and only if
(Multiple Choice)
4.9/5  (33)
(33)
Any categorical syllogism with two affirmative premises is valid.
(True/False)
4.8/5  (41)
(41)
The following categorical argument form has more than three terms: "No non-M are P. Some S are non-M. So, no S are non-P." Reduce the terms to three by removing term-complements via applications of conversion, obversion, and/or contraposition.
(Essay)
4.9/5  (38)
(38)
A fallacy of illicit minor is a violation of which of the following rules for evaluating categorical syllogisms? In a valid standard-form categorical syllogism¼
(Multiple Choice)
4.8/5  (34)
(34)
Rewrite the following argument as a standard-form categorical syllogism; then identify its mood and figure: Since some science professors are absent-minded persons and all philosophers are absent-minded persons, some scientists are not philosophers.
(Short Answer)
4.9/5  (45)
(45)
The following categorical argument form has more than three terms: "All non-P are M. Some S are non-M. So, no non-S are P." Reduce the terms to three by removing term-complements via applications of conversion, obversion, and/or contraposition.
(Essay)
4.8/5  (39)
(39)
Which of the following immediate inferences is invalid according to modern categorical logic?
(Multiple Choice)
4.8/5  (33)
(33)
Which of the five rules for evaluating syllogisms can you use to determine whether the following form is valid?
All M are P. No S are M. So, no S are P.
(Essay)
4.9/5  (35)
(35)
Put the following categorical syllogism into standard form and identify its mood and figure.
All professional wrestlers are good actors, because some good actors are not powerful athletes and all professional wrestlers are powerful athletes.
(Short Answer)
4.8/5  (42)
(42)
Put the following categorical syllogism into standard form and identify its mood and figure.
No tragic actors are idiots. But some comedians are not idiots. So, some comedians are not tragic actors.
(Short Answer)
4.8/5  (40)
(40)
Rewrite the following argument as a standard-form categorical syllogism; then identify its mood and figure: No knights are shrubberies, since no shrubberies are jousters and all jousters are knights.
(Short Answer)
4.9/5  (40)
(40)
Showing 61 - 80 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)