Exam 3: Truth Tables
Exam 1: Introduction10 Questions
Exam 2: Symbolizing in Sentential Logic24 Questions
Exam 3: Truth Tables27 Questions
Exam 4: Proofs Without CP or IP9 Questions
Exam 5: Proofs With CP or IP12 Questions
Exam 6: Sentential Logic Truth Trees8 Questions
Exam 7: Predicate Logic Symbolization29 Questions
Exam 8: Predicate Logic Semantics9 Questions
Exam 9: Predicate Logic Proofs8 Questions
Exam 10: Relational Predicate Logic38 Questions
Exam 11: Quantifier Rules Theory8 Questions
Exam 12: Predicate Logic Truth Trees8 Questions
Exam 13: Identity22 Questions
Exam 14: Syllogistic Logic32 Questions
Exam 15: Informal Fallacies10 Questions
Exam 16: Inductive Logic14 Questions
Exam 17: Axiom Systems11 Questions
Select questions type
Logical Equivalences
Use a truth table to determine which of the following pairs of sentence forms are logically equivalent.
-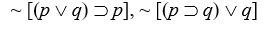
Free
(Short Answer)
4.8/5  (39)
(39)
Correct Answer:
Not Equivalent
General Theory
-Assume you know of an argument only that its premises are not consistent. What, if anything, can you tell about the argument's validity? (Defend your answer.)
Free
(Short Answer)
4.7/5  (39)
(39)
Correct Answer:
If an argument's premises are not consistent then it will be impossible for all of them to be true. Therefore, the argument must be valid, because it will be impossible for the premises to be true and the conclusion false.
General Theory
-Suppose one of the premises of an argument is logic equivalent to the conclusion. What, if anything, can you conclude about the argument's validity?
Free
(Short Answer)
4.9/5  (38)
(38)
Correct Answer:
If one of the premises of an argument is logically equivalent to the conclusion, then the premise and the conclusion will always have the same truth value. Thus, it will be impossible for that argument to have all true premises and a false conclusion, and so it will be valid.
General Theory
-If a sentence form contains five variables, how many lines or rows must its complete truth table analysis have?
(Short Answer)
4.7/5  (43)
(43)
General Theory
-a. We can define a tautologous sentence as one that is a substitution instance of some tautologous sentence form, and a contradictory sentence as one that is a substitution instance of some contradictory sentence form. Why can't we analogously define a contingent sentence as one that is a substitution instance of some contingent sentence form? (Defend your answer, including examples.)
b. We cannot define a contingent sentence as one that is a substitution instance of some contingent sentence form. But then how can we define that term?
(Short Answer)
4.9/5  (37)
(37)
Tautologies, Contradictions, and Contingent Sentences
Determine by truth table analysis which of the following sentence forms are tautologous, which are contradictory, and which are contingent:
-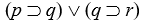
(Short Answer)
4.8/5  (33)
(33)
Short Truth Table Test for Consistency
Use the short truth table method to show that the following sets of premises are consistent:
-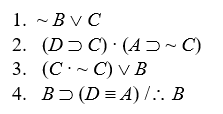
(Short Answer)
4.8/5  (42)
(42)
Logical Equivalences
Use a truth table to determine which of the following pairs of sentence forms are logically equivalent.
-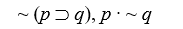
(Short Answer)
4.8/5  (33)
(33)
General Theory
-Determine the sentence forms of which the following are substitution instances:
a. 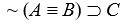 b.
b. 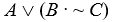
(Short Answer)
4.9/5  (35)
(35)
Tautologies, Contradictions, and Contingent Sentences
Determine by truth table analysis which of the following sentence forms are tautologous, which are contradictory, and which are contingent:
-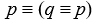
(Short Answer)
4.7/5  (36)
(36)
Short Truth Table Test for Consistency
Use the short truth table method to show that the following sets of premises are consistent:
-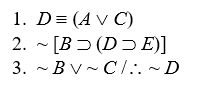
(Short Answer)
4.8/5  (23)
(23)
Logical Equivalences
Use a truth table to determine which of the following pairs of sentence forms are logically equivalent.
-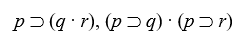
(Short Answer)
4.8/5  (31)
(31)
Logical Equivalences
Use a truth table to determine which of the following pairs of sentence forms are logically equivalent.
-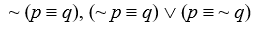
(Short Answer)
4.8/5  (37)
(37)
Short Truth Table Test for Invalidity
Use the short truth table method to show that the following arguments are invalid:
-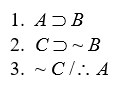
(Short Answer)
4.7/5  (35)
(35)
Short Truth Table Test for Consistency
Use the short truth table method to show that the following sets of premises are consistent:
-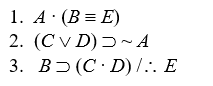
(Short Answer)
4.9/5  (29)
(29)
Tautologies, Contradictions, and Contingent Sentences
Determine by truth table analysis which of the following sentence forms are tautologous, which are contradictory, and which are contingent:
-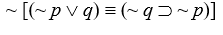
(Short Answer)
5.0/5  (33)
(33)
Tautologies, Contradictions, and Contingent Sentences
Determine by truth table analysis which of the following sentence forms are tautologous, which are contradictory, and which are contingent:
-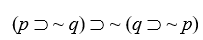
(Short Answer)
4.7/5  (38)
(38)
Short Truth Table Test for Invalidity
Use the short truth table method to show that the following arguments are invalid:
-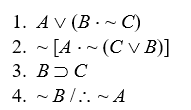
(Short Answer)
4.8/5  (40)
(40)
Short Truth Table Test for Consistency
Use the short truth table method to show that the following sets of premises are consistent:
-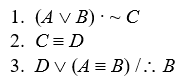
(Short Answer)
4.9/5  (38)
(38)
Short Truth Table Test for Invalidity
Use the short truth table method to show that the following arguments are invalid:
-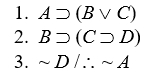
(Short Answer)
4.8/5  (42)
(42)
Showing 1 - 20 of 27
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)