Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 11: Differential Equations

arrow
Exam 1: Functions, graphs, and Limits427 Questionsadd course
Exam 2: Differentiation84 Questionsadd course
Exam 3: Applications of the Derivative122 Questionsadd course
Exam 4: Exponential and Logarithmic Functions122 Questionsadd course
Exam 5: Integration and Its Applications88 Questionsadd course
Exam 6: Techniques of Integration46 Questionsadd course
Exam 7: Functions of Several Variables113 Questionsadd course
Exam 8: Trigonometric Functions60 Questionsadd course
Exam 9: Probability and Calculus36 Questionsadd course
Exam 10: Series and Taylor Polynomials104 Questionsadd course
Exam 11: Differential Equations77 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

​Find the general solution of the first-order linear differential equation. ​ ​ ​Find the general solution of the first-order linear differential equation. ​ ​ ​ ​

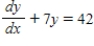
Free
(Multiple Choice)
4.8/5
(46)
Question 1
Correct Answer:
Verified

B

Verify that the general solution satisfies the differential equation.Then find the particular solution that satisfies the initial condition. ​ Verify that the general solution satisfies the differential equation.Then find the particular solution that satisfies the initial condition. ​

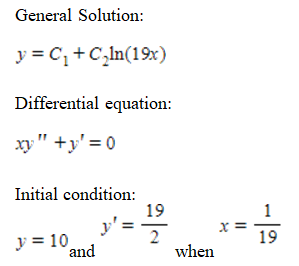
Free
(Multiple Choice)
4.7/5
(38)
Question 2
Correct Answer:
Verified

A

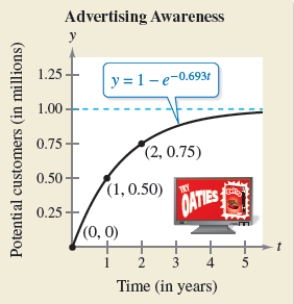
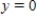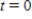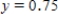Use the advertising awareness model described to find the number of people y (in millions)aware of the product as a function of time ​t (in years). ​ Use the advertising awareness model described to find the number of people y (in millions)aware of the product as a function of time ​t (in years). ​ when ; when ​ ​ when Use the advertising awareness model described to find the number of people y (in millions)aware of the product as a function of time ​t (in years). ​ when ; when ​ ​ ; Use the advertising awareness model described to find the number of people y (in millions)aware of the product as a function of time ​t (in years). ​ when ; when ​ ​ when Use the advertising awareness model described to find the number of people y (in millions)aware of the product as a function of time ​t (in years). ​ when ; when ​ ​ ​ Use the advertising awareness model described to find the number of people y (in millions)aware of the product as a function of time ​t (in years). ​ when ; when ​ ​ ​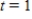

Free
(Multiple Choice)
4.8/5
(38)
Question 3
Correct Answer:
Verified

E

Assume that the rate of change in Assume that the rate of change in is proportional to Solve the resulting differential equation and find the particular solution that passes through the points , ​ is proportional to Assume that the rate of change in is proportional to Solve the resulting differential equation and find the particular solution that passes through the points , ​ Solve the resulting differential equation Assume that the rate of change in is proportional to Solve the resulting differential equation and find the particular solution that passes through the points , ​ and find the particular solution that passes through the points Assume that the rate of change in is proportional to Solve the resulting differential equation and find the particular solution that passes through the points , ​ , Assume that the rate of change in is proportional to Solve the resulting differential equation 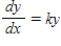and find the particular solution that passes through the points , ​ ​

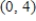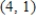
(Multiple Choice)
5.0/5
(30)
Question 4

​Find the general solution of the first-order linear differential equation. ​ ​ ​Find the general solution of the first-order linear differential equation. ​ ​ ​ ​

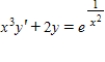
(Multiple Choice)
4.8/5
(31)
Question 5

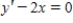Find the solution of the differential equation Find the solution of the differential equation ,without solving it. ​ ,without solving it. ​

(Multiple Choice)
4.9/5
(36)
Question 6

Use the chemical reaction model described to find the amount y (in grams)as a function of time ​t (in hours).Then use a graphing utility to graph the function. ​ Use the chemical reaction model described to find the amount y (in grams)as a function of time ​t (in hours).Then use a graphing utility to graph the function. ​ grams when ; grams when ​ ​ ​ grams when Use the chemical reaction model described to find the amount y (in grams)as a function of time ​t (in hours).Then use a graphing utility to graph the function. ​ grams when ; grams when ​ ​ ​ ; Use the chemical reaction model described to find the amount y (in grams)as a function of time ​t (in hours).Then use a graphing utility to graph the function. ​ grams when ; grams when ​ ​ ​ grams when ​ Use the chemical reaction model described to find the amount y (in grams)as a function of time ​t (in hours).Then use a graphing utility to graph the function. ​ grams when ; grams when ​ ​ ​ ​ Use the chemical reaction model described to find the amount y (in grams)as a function of time ​t (in hours).Then use a graphing utility to graph the function. ​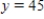 grams when 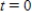; 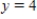grams when ​ ​ ​ ​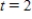

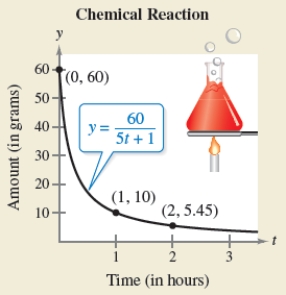
(Multiple Choice)
4.9/5
(31)
Question 7

Assume that the rate of change in y is proportional to ​y.Solve the resulting differential equation Assume that the rate of change in y is proportional to ​y.Solve the resulting differential equation and find the particular solution that passes through the points , ​ and find the particular solution that passes through the points Assume that the rate of change in y is proportional to ​y.Solve the resulting differential equation and find the particular solution that passes through the points , ​ , Assume that the rate of change in y is proportional to ​y.Solve the resulting differential equation 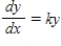and find the particular solution that passes through the points , ​ ​

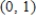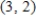
(Multiple Choice)
4.7/5
(40)
Question 8

During a chemical reaction,a compound changes into another compound at a rate proportional to the unchanged amount ​y.Write the differential equation for the chemical reaction model.Find the particular solution when the initial amount of the original compound is 20 grams and the amount remaining after 1 hour is 16 grams. ​

(Multiple Choice)
4.9/5
(38)
Question 9

​Use the integration to find the general solution of the differential equation ​Use the integration to find the general solution of the differential equation ​ ​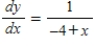

(Multiple Choice)
4.8/5
(41)
Question 10

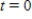​A large corporation starts at time ​A large corporation starts at time to invest part of its profit at a rate of P dollars per year in a fund for future expansion.Assume that the fund earns r percent interest per year compounded continuously.The rate of growth of the amount A in the fund is given by where when and r is in decimal form.Solve this differential equation for A as a function of ​t. 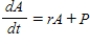​ to invest part of its profit at a rate of P dollars per year in a fund for future expansion.Assume that the fund earns r percent interest per year compounded continuously.The rate of growth of the amount A in the fund is given by ​A large corporation starts at time to invest part of its profit at a rate of P dollars per year in a fund for future expansion.Assume that the fund earns r percent interest per year compounded continuously.The rate of growth of the amount A in the fund is given by where when and r is in decimal form.Solve this differential equation for A as a function of ​t. 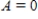​ where ​A large corporation starts at time to invest part of its profit at a rate of P dollars per year in a fund for future expansion.Assume that the fund earns r percent interest per year compounded continuously.The rate of growth of the amount A in the fund is given by where when and r is in decimal form.Solve this differential equation for A as a function of ​t. 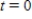​ when ​A large corporation starts at time to invest part of its profit at a rate of P dollars per year in a fund for future expansion.Assume that the fund earns r percent interest per year compounded continuously.The rate of growth of the amount A in the fund is given by where when and r is in decimal form.Solve this differential equation for A as a function of ​t. ​ and r is in decimal form.Solve this differential equation for A as a function of ​t. ​

(Multiple Choice)
4.9/5
(27)
Question 11

Find the solution of the differential equation Find the solution of the differential equation 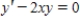,without solving it. ​ ,without solving it. ​

(Multiple Choice)
4.8/5
(38)
Question 12

​A 200-gallon tank is full of a solution containing 55 pounds of concentrate.Starting at time t=0 ,distilled water is added to the tank at a rate of 20 gallons per minute,and the well-stirred solution is withdrawn at the same rate.Find the amount of concentrate Q in the solution as a function of ​t. ​

(Multiple Choice)
4.9/5
(41)
Question 13

​Use separation of variables to find the general solution of the differential equation. ​ ​Use separation of variables to find the general solution of the differential equation. ​ ​ ​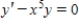

(Multiple Choice)
4.8/5
(25)
Question 14

The rate of change of the population of a city is proportional to the population ​P at any time (in years).In 2000,the population was 200,000,and the constant of proportionality was 0.015.Estimate the population of the city in the year 2020. ​

(Multiple Choice)
4.8/5
(29)
Question 15

Find the particular solution that satisfies the initial condition. Find the particular solution that satisfies the initial condition. ; Initial Condition: when ​ ; Initial Condition: Find the particular solution that satisfies the initial condition. 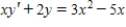; Initial Condition: 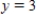when ​ when Find the particular solution that satisfies the initial condition. ; Initial Condition: when ​ ​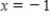

(Multiple Choice)
4.9/5
(40)
Question 16

​Use separation of variables to find the general solution of the differential equation. ​ ​Use separation of variables to find the general solution of the differential equation. ​ ​ ​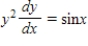

(Multiple Choice)
4.8/5
(40)
Question 17

​Solve for ​y in two ways. ​ ​ ​Solve for ​y in two ways. ​ ​ ​ ​

(Multiple Choice)
4.8/5
(34)
Question 18

Find an equation of the graph that passes through the point and has the specified slope.Then graph the equation. ​ Point: Find an equation of the graph that passes through the point and has the specified slope.Then graph the equation. ​ Point: 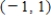, Slope: , Slope: Find an equation of the graph that passes through the point and has the specified slope.Then graph the equation. ​ Point: , Slope: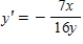

(Multiple Choice)
4.8/5
(37)
Question 19

​Find the general solution of the first-order linear differential equation. ​ ​ ​Find the general solution of the first-order linear differential equation. ​ ​ ​ ​

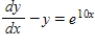
(Multiple Choice)
4.8/5
(31)
Question 20
Showing 1 - 20 of 77
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)