Exam 12: Electing the President
Exam 1: Urban Services107 Questions
Exam 2: Business Efficiency104 Questions
Exam 3: Planning and Scheduling108 Questions
Exam 4: Linear Programming111 Questions
Exam 5: Exploring Data: Distributions115 Questions
Exam 6: Exploring Data: Relationships104 Questions
Exam 7: Data for Decisions99 Questions
Exam 8: Probability: the Mathematics of Chance108 Questions
Exam 9: Social Choice: the Impossible Dream103 Questions
Exam 10: The Manipulability of Voting Systems106 Questions
Exam 11: Weighted Voting Systems111 Questions
Exam 12: Electing the President93 Questions
Exam 13: Fair Division121 Questions
Exam 14: Apportionment112 Questions
Exam 15: Game Theory: the Mathematics of Competition113 Questions
Exam 16: Identification Numbers110 Questions
Exam 17: Information Science94 Questions
Exam 18: Growth and Form111 Questions
Exam 19: Symmetry and Patterns115 Questions
Exam 20: Tilings112 Questions
Exam 21: Savings Models113 Questions
Exam 22: Borrowing Models113 Questions
Exam 23: The Economics of Resources119 Questions
Select questions type
Use the following distribution of 31 voters at seven different positions over the interval [0, 1] to answer the Questions Position 0.1 0.2 0.3 0.4 0.5 0.7 0.8 Number of voters 1 4 5 6 5 6 4
-For two candidates A and B with distinct policy positions 0.3 and 0.75, respectively, find the number of votes for the candidate A based on voter's ideal positions.
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
D
Consider the following distribution of 34 voters at eight different positions over the interval [0, 1]. Location 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Number of voters 2 3 3 2 5 7 8 4 This distribution of voters is best described as:
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
A
Use the following information to answer Questions
Consider the following distribution of 34 voters at eight different positions over the interval [0, 1]. Location 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Number of voters 2 3 5 7 7 5 3 2
-Assume that Candidate A and Candidate B's policy positions are 0.3 and 0.8. If Candidate C enters at 0.55, what fraction of the vote does the winner receive?
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
B
A distribution of voters is symmetric and unimodal, and the first two candidates have chosen different positions, A and B, that are equidistant from the median. A is below the median and B is above the median, and two thirds of the voters lie between A and B. To win the election, a third candidate should take a position C that lies:
(Multiple Choice)
4.9/5  (28)
(28)
Use the following information to answer the Questions
Suppose 36 voters are distributed at nine different positions over the interval [0, 1], as suggested by this incomplete table. Location 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Number of voters ? ? ? ? ? ? ? ? ?
-Which situation below would result in a symmetric distribution?
(Multiple Choice)
5.0/5  (38)
(38)
Use the following information to answer the Questions
Seven board members of a company must decide between two other board members (A and B) for a certain position. The voters are concerned with two issues and their ideal points are represented as ordered pairs: (1, 5), (3, 3), (5, 2), (6, 4), (6, 2), (4, 4), and (3, 2). Assume that A and B announce policy positions of (2, 2) and (5, 4), respectively.
-Find the number of board members who would vote for A based on ideal points.
(Short Answer)
4.8/5  (32)
(32)
Use the following information to answer the Questions.
Consider the following distribution of 33 voters at eight different positions over the interval [0,1]. Position 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Number of voters 6 2 2 1 1 2 2 4 1
-For two candidates A and B with distinct policy positions 0.3 and 0.75, respectively, find the number of votes for the candidate A based on voter's ideal positions.
(Short Answer)
4.8/5  (25)
(25)
Use the following to answer the Questions
Suppose that the continuous distribution of voters' ideal points is the bent solid line below. 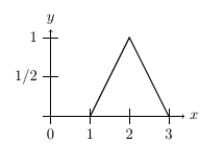 -Assuming that Candidate A's policy position is 1.5 and Candidate B announces a policy position of 2.3, which voters would vote for Candidate B?
-Assuming that Candidate A's policy position is 1.5 and Candidate B announces a policy position of 2.3, which voters would vote for Candidate B?
(Multiple Choice)
4.8/5  (28)
(28)
Suppose 16 voters are distributed at different positions over the interval [0, 1], as shown below. Location 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Number of voters 2 0 4 5 4 1 0 0 0 What can you say about the distribution?
(Multiple Choice)
4.9/5  (25)
(25)
Use the following information to answer the Questions
Suppose 36 voters are distributed at nine different positions over the interval [0, 1], as suggested by this incomplete table. Location 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 Number of voters ? ? ? ? ? ? ? ? ?
-Which situation below would result in a bimodal distribution?
(Multiple Choice)
4.8/5  (30)
(30)
A distribution of voters is symmetric and unimodal, and the first two candidates have chosen different positions, A and B, that are equidistant from the median. A is below the median and B is above the median. No more than one third of the voters lie between A and B. To win the election, a third candidate should take a position C that lies:
(Multiple Choice)
4.8/5  (40)
(40)
Use the following information to answer the Questions
Seven board members of a company must decide between two other board members (A and B) for a certain position. The voters are concerned with two issues and their ideal points are represented as ordered pairs: (1, 4), (2, 3), (5, 2), (6, 3), (6, 1), (4, 4), and (3, 3). Assume that A and B announce policy positions of (1, 1) and (6, 4), respectively.
-What is the equation of the line passing through candidates' policy positions?
(Multiple Choice)
4.9/5  (34)
(34)
Use the following to answer the Questions
Suppose that the continuous distribution of voters' ideal points is the bent solid line below.  -Assume that Candidate A and Candidate B's policy positions are 1.5 and 2.5. If Candidate C enters at 1, what fraction of the vote does the winner receive?
-Assume that Candidate A and Candidate B's policy positions are 1.5 and 2.5. If Candidate C enters at 1, what fraction of the vote does the winner receive?
(Multiple Choice)
4.8/5  (34)
(34)
Use the following information to answer the Questions
Suppose that the continuous distribution of voters' ideal points is the bent solid line below. 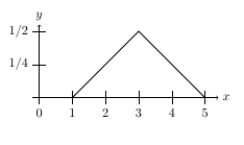 -Assuming that Candidate A's policy position is 4, if Candidate B announces a policy position between 1 and 2, then who will be the winner of the election?
-Assuming that Candidate A's policy position is 4, if Candidate B announces a policy position between 1 and 2, then who will be the winner of the election?
(Short Answer)
4.8/5  (33)
(33)
Showing 1 - 20 of 93
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)