Deck 21: Calculus-Based Optimization
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/24
Play
Full screen (f)
Deck 21: Calculus-Based Optimization
1
At a minimum of a nonlinear function,the first derivative is equal to zero,and the second derivative is positive.
True
2
If,for a nonlinear function,the first derivative is equal to zero and the second derivative is equal to zero,we have both a maximum and a minimum occurring simultaneously.
False
3
The derivative of 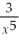 is
is
A)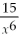
B)-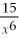
C)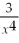
D)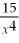
E)None of the above
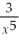 is
isA)
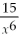
B)-
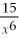
C)
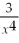
D)
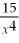
E)None of the above
B
4
The slope of a straight line is constant when measured at any point along the line.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
5
A zero value for the derivative of a nonlinear function always indicates the location of a maximum or minimum.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
6
The derivative of 5x3 + 3x2 + 7x + 9 is
A)15X2 + 6x + 7.
B)6x2 + 7x + 9.
C)5x2 + 3x + 7.
D)3x2 + 2x + 7.
E)None of the above
A)15X2 + 6x + 7.
B)6x2 + 7x + 9.
C)5x2 + 3x + 7.
D)3x2 + 2x + 7.
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
7
To determine the slope of a nonlinear function at a point,we must find the slope of a line tangent to the point.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
8
The first step in attempting to find a minimum or maximum of a nonlinear function is to take the derivative of the function,set it equal to zero,and solve for x.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
9
The critical point for the function y = 7x2 - 7x + 4 lies at
A)x = -1.
B)x = 1.
C)x = -1/2.
D)x = 1/2.
E)None of the above
A)x = -1.
B)x = 1.
C)x = -1/2.
D)x = 1/2.
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
10
Find the point at which the following function is a maximum: 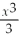 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
A)x = 3
B)x = 1
C)x = 0
D)x = -3
E)None of the above
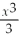 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.A)x = 3
B)x = 1
C)x = 0
D)x = -3
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
11
The second derivative tells about the slope of the first derivative.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
12
The derivative of a constant is one.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
13
The second derivative of 7x4 + 6x3 + 5x + 3 is
A)7x3 + 6x2 + 5.
B)28x3 + 18x2 + 5x + 3.
C)28x3 + 18x2 + 5.
D)84x2 + 36x.
E)None of the above
A)7x3 + 6x2 + 5.
B)28x3 + 18x2 + 5x + 3.
C)28x3 + 18x2 + 5.
D)84x2 + 36x.
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
14
The EOQ model is obtained by taking the second derivative of the revenue function.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
15
To maximize total revenues,one can set the derivative of the total revenue function equal to zero and solve.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
16
We can find a point of inflection by simply setting the second derivative of the nonlinear function equal to zero and solving.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
17
The slope of a nonlinear function varies depending on the point along the line at which it is measured.

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
18
The derivative of 2x2 + 2x + 7 is
A)2x + 2.
B)1x + 7.
C)4x + 2.
D)x2 + 7.
E)None of the above
A)2x + 2.
B)1x + 7.
C)4x + 2.
D)x2 + 7.
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
19
The critical point for the function y = 3x2 + 5x + 2 is at
A)x = -5/6.
B)x = 3/5.
C)x = -3/2.
D)There is no critical point
E)None of the above
A)x = -5/6.
B)x = 3/5.
C)x = -3/2.
D)There is no critical point
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
20
The derivative of 19x4 + 2x3 + 5x2 + 1x + 9 is
A)19x3 + 2x2 + 5x + 1.
B)4x3 + 3x2 + 2x + 1.
C)12x2 + 6x + 9.
D)76x3 + 6x2 + 10x + 1.
E)None of the above
A)19x3 + 2x2 + 5x + 1.
B)4x3 + 3x2 + 2x + 1.
C)12x2 + 6x + 9.
D)76x3 + 6x2 + 10x + 1.
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
21
Profit for the Dew Drop Inn Country Diner is given by p = -0.1q2 + 1.80q + 100,where p is profit and q is the number of customers.What number of customers maximizes profit?
A)100
B)900
C)300
D)9
E)None of the above
A)100
B)900
C)300
D)9
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
22
Find the point at which the following function is a minimum: y = 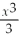 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
A)x = 3
B)x = 1
C)x = 0
D)x = -3
E)None of the above
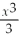 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.A)x = 3
B)x = 1
C)x = 0
D)x = -3
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
23
Find the point at which the following function has an inflection point: y = 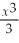 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
A)3
B)1
C)2
D)0
E)None of the above
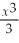 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.A)3
B)1
C)2
D)0
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck
24
Find the critical point for the function y = X3 + 60.This point is a(n)
A)maximum.
B)minimum.
C)inflection point.
D)Could be any of the above
E)None of the above
A)maximum.
B)minimum.
C)inflection point.
D)Could be any of the above
E)None of the above

Unlock Deck
Unlock for access to all 24 flashcards in this deck.
Unlock Deck
k this deck


