Exam 21: Calculus-Based Optimization
Exam 1: Introduction to Quantitative Analysis71 Questions
Exam 2: Probability Concepts and Applications157 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models133 Questions
Exam 5: Forecasting111 Questions
Exam 6: Inventory Control Models123 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods110 Questions
Exam 8: Linear Programming Applications105 Questions
Exam 9: Transportation,assignment,and Network Models98 Questions
Exam 10: Integer Programming,goal Programming,and Nonlinear Programming98 Questions
Exam 11: Project Management134 Questions
Exam 12: Waiting Lines and Queuing Theory Models145 Questions
Exam 13: Simulation Modeling79 Questions
Exam 14: Markov Analysis86 Questions
Exam 15: Statistical Quality Control98 Questions
Exam 16: Analytic Hierarchy Process53 Questions
Exam 17: Dynamic Programming67 Questions
Exam 18: Decision Theory and the Normal Distribution50 Questions
Exam 19: Game Theory47 Questions
Exam 20: Mathematical Tools: Determinants and Matrices99 Questions
Exam 21: Calculus-Based Optimization24 Questions
Exam 22: Linear Programming: The Simplex Method100 Questions
Exam 23: Transportation, Assignment, and Network Algorithms111 Questions
Select questions type
The second derivative tells about the slope of the first derivative.
Free
(True/False)
4.7/5  (40)
(40)
Correct Answer:
True
The second derivative of 7x4 + 6x3 + 5x + 3 is
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
D
Find the point at which the following function is a maximum: 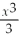 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
(Multiple Choice)
4.9/5  (35)
(35)
Find the point at which the following function is a minimum: y = 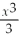 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
(Multiple Choice)
4.9/5  (30)
(30)
Find the point at which the following function has an inflection point: y = 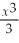 - 2x2 + 3x + 6.
- 2x2 + 3x + 6.
(Multiple Choice)
4.8/5  (37)
(37)
To maximize total revenues,one can set the derivative of the total revenue function equal to zero and solve.
(True/False)
4.8/5  (40)
(40)
The EOQ model is obtained by taking the second derivative of the revenue function.
(True/False)
4.7/5  (37)
(37)
The slope of a nonlinear function varies depending on the point along the line at which it is measured.
(True/False)
4.8/5  (33)
(33)
Profit for the Dew Drop Inn Country Diner is given by p = -0.1q2 + 1.80q + 100,where p is profit and q is the number of customers.What number of customers maximizes profit?
(Multiple Choice)
4.9/5  (34)
(34)
Find the critical point for the function y = X3 + 60.This point is a(n)
(Multiple Choice)
4.8/5  (36)
(36)
To determine the slope of a nonlinear function at a point,we must find the slope of a line tangent to the point.
(True/False)
4.8/5  (33)
(33)
If,for a nonlinear function,the first derivative is equal to zero and the second derivative is equal to zero,we have both a maximum and a minimum occurring simultaneously.
(True/False)
4.8/5  (34)
(34)
A zero value for the derivative of a nonlinear function always indicates the location of a maximum or minimum.
(True/False)
4.9/5  (38)
(38)
At a minimum of a nonlinear function,the first derivative is equal to zero,and the second derivative is positive.
(True/False)
4.8/5  (35)
(35)
The first step in attempting to find a minimum or maximum of a nonlinear function is to take the derivative of the function,set it equal to zero,and solve for x.
(True/False)
4.8/5  (35)
(35)
Showing 1 - 20 of 24
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)