Deck 17: The Nature of Voting and Apportionment
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/52
Play
Full screen (f)
Deck 17: The Nature of Voting and Apportionment
1
Use Jefferson's plan. Which state does violate the quota rule? 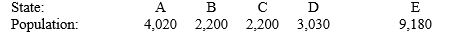 Number of seats:
Number of seats:  200
200
A) B
B) D
C) E
D) A
E) none
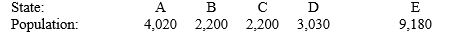 Number of seats:
Number of seats:  200
200
A) B
B) D
C) E
D) A
E) none
E
2
Apportion the indicated number of representatives to two states, A, and B, using Hamilton's plan. Next, recalculate the apportionment using Hamilton's plan for the three states, C and the original states. Decide whether the new states paradox occurs. 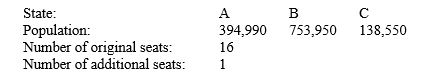
A) C illustrates the new states paradox.
B) A illustrates the new states paradox.
C) A and C illustrate the new states paradox.
D) B illustrates the new states paradox.
E) The paradox does not occur.
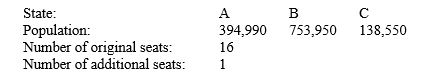
A) C illustrates the new states paradox.
B) A illustrates the new states paradox.
C) A and C illustrate the new states paradox.
D) B illustrates the new states paradox.
E) The paradox does not occur.
A illustrates the new states paradox.
3
An elderly rancher died and left her estate to her three children. She bequeathed her 35 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. The judge arrived with a horse of his own. He put his horse in with the 35 belonging to the estate, and then told each child to pick from among the 36 in the proportions stipulated by the will (but be careful, he warned, not to pick his horse). The first child took eighteen horses, the second child took twelve, and the third child, four. The 35 horses were thus divided among the children. The wise judge took his horse from the corral, took a fair sum for his services, and rode off into the sunset.
The youngest son complained that the oldest son received 18 horses (but was entitled to only 35/2 = 17.5 horses). The judge was asked about this, and he faxed the children the following message: "You all received more than you deserved. The eldest received 1/2 of an 'extra' horse, the middle child received 1/3 more, and the youngest, 1/9 of a horse 'extra.'" Apportion the horses according to Adams', Jefferson's, and Webster's plans. Which plan gives the appropriate distribution of horses?
__________ (Adams' plan and Jefferson's plan, Webster's plan and Jefferson's plan, Adams' plan and Webster's plan, Adams' plan, None of the plans)
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. The judge arrived with a horse of his own. He put his horse in with the 35 belonging to the estate, and then told each child to pick from among the 36 in the proportions stipulated by the will (but be careful, he warned, not to pick his horse). The first child took eighteen horses, the second child took twelve, and the third child, four. The 35 horses were thus divided among the children. The wise judge took his horse from the corral, took a fair sum for his services, and rode off into the sunset.
The youngest son complained that the oldest son received 18 horses (but was entitled to only 35/2 = 17.5 horses). The judge was asked about this, and he faxed the children the following message: "You all received more than you deserved. The eldest received 1/2 of an 'extra' horse, the middle child received 1/3 more, and the youngest, 1/9 of a horse 'extra.'" Apportion the horses according to Adams', Jefferson's, and Webster's plans. Which plan gives the appropriate distribution of horses?
__________ (Adams' plan and Jefferson's plan, Webster's plan and Jefferson's plan, Adams' plan and Webster's plan, Adams' plan, None of the plans)
None of the plans
4
Use Jefferson's plan. Which state does violate the quota rule? 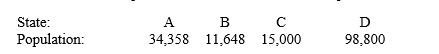 Number of seats:
Number of seats:  200
200
__________ (A, B, C, D, none)
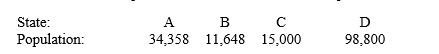 Number of seats:
Number of seats:  200
200
__________ (A, B, C, D, none)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
5
Use Hamilton's plan to apportion the new seats to the existing states. Then increase the number of seats by one and decide whether the Alabama paradox occurs. Assume that the populations are in thousands.  Number of seats:
Number of seats:  86
86
A) C illustrates Alabama paradox.
B) A illustrates Alabama paradox.
C) D illustrates Alabama paradox.
D) The Alabama paradox does not occur.
E) B illustrates Alabama paradox.
 Number of seats:
Number of seats:  86
86
A) C illustrates Alabama paradox.
B) A illustrates Alabama paradox.
C) D illustrates Alabama paradox.
D) The Alabama paradox does not occur.
E) B illustrates Alabama paradox.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
6
An elderly rancher died and left her estate to her three children. She bequeathed her 17 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. They informed the judge that the 17 horses were not of equal value. The children agreed on a ranking of the 17 horses (#1 being the best and #17 being a real dog of a horse). They asked the judge to divide the estate fairly so that each child would receive not only the correct number of horses but horses whose average rank would also be the same. For example, if a child received horses 1 and 17, the number of horses is two and the average value is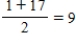 . How did the judge apportion the horses?
. How did the judge apportion the horses?
A) Eldest: 2, 5, 4, 7, 11, 12, 13, 14, and 15; middle: 3, 6, 8, 9, 10, and 16; youngest: 1 and 17.
B) Eldest: 2, 3, 4, 8, 11, 12, 13, 14, and 17; middle: 5, 6, 7, 9, 10, and 16; youngest: 1 and 15.
C) Eldest: 1, 2, 4, 7, 11, 12, 13, 14, and 15; middle: 5, 6, 8, 9, 10, and 16; youngest: 3 and 17.
D) Eldest: 2, 3, 4, 7, 11, 12, 13, 14, and 15; middle: 5, 6, 8, 9, 10, and 16; youngest: 1 and 17.
E) Eldest: 2, 3, 4, 7, 11, 12, 13, 14, and 17; middle: 5, 6, 8, 9, 10, and 16; youngest: 1 and 15.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. They informed the judge that the 17 horses were not of equal value. The children agreed on a ranking of the 17 horses (#1 being the best and #17 being a real dog of a horse). They asked the judge to divide the estate fairly so that each child would receive not only the correct number of horses but horses whose average rank would also be the same. For example, if a child received horses 1 and 17, the number of horses is two and the average value is
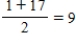 . How did the judge apportion the horses?
. How did the judge apportion the horses?
A) Eldest: 2, 5, 4, 7, 11, 12, 13, 14, and 15; middle: 3, 6, 8, 9, 10, and 16; youngest: 1 and 17.
B) Eldest: 2, 3, 4, 8, 11, 12, 13, 14, and 17; middle: 5, 6, 7, 9, 10, and 16; youngest: 1 and 15.
C) Eldest: 1, 2, 4, 7, 11, 12, 13, 14, and 15; middle: 5, 6, 8, 9, 10, and 16; youngest: 3 and 17.
D) Eldest: 2, 3, 4, 7, 11, 12, 13, 14, and 15; middle: 5, 6, 8, 9, 10, and 16; youngest: 1 and 17.
E) Eldest: 2, 3, 4, 7, 11, 12, 13, 14, and 17; middle: 5, 6, 8, 9, 10, and 16; youngest: 1 and 15.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
7
Use Jefferson's plan. Which state does violate the quota rule? 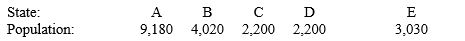 Number of seats:
Number of seats:  200
200
__________ (A, B, C, D, E, none)
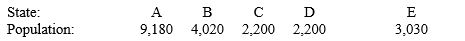 Number of seats:
Number of seats:  200
200
__________ (A, B, C, D, E, none)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
8
A fair apportionment of dividing a leftover piece of cake between two children is to let child #1 cut the cake into two pieces and then to let child #2 pick which piece he or she wants. Consider the following apportionment of dividing the leftover piece of cake among three children. Let the first child cut the cake into two pieces. Then the second child is permitted to cut one of those pieces into two parts. Child #3 can select any of the pieces, followed by child #1 selecting one of the remaining pieces, followed by child #2 who gets the remaining piece. Is this allocation process fair if each child's goal is to maximize the size of his or her own piece of cake?
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
9
An elderly rancher died and left her estate to her three children. She bequeathed her 17 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. They informed the judge that the 17 horses were not of equal value. The children agreed on a ranking of the 17 horses (#1 being the best and #17 being a real dog of a horse). They asked the judge to divide the estate fairly so that each child would receive not only the correct number of horses but horses whose average rank would also be the same. For example, if a child received horses 1 and 17, the number of horses is two and the average value is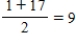 . How did the judge apportion the horses?
. How did the judge apportion the horses?
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. They informed the judge that the 17 horses were not of equal value. The children agreed on a ranking of the 17 horses (#1 being the best and #17 being a real dog of a horse). They asked the judge to divide the estate fairly so that each child would receive not only the correct number of horses but horses whose average rank would also be the same. For example, if a child received horses 1 and 17, the number of horses is two and the average value is
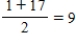 . How did the judge apportion the horses?
. How did the judge apportion the horses?
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
10
An elderly rancher died and left her estate to her three children. She bequeathed her 71 prize horses in the following manner: 1/2 to the eldest, 1/3 to the second child, and 1/9 to the youngest.
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. The judge arrived with a horse of his own. He put his horse in with the 71 belonging to the estate, and then told each child to pick from among the 72 in the proportions stipulated by the will (but be careful, he warned, not to pick his horse). The first child took thirty six horses, the second child took twenty four, and the third child, eight. The 71 horses were thus divided among the children. The wise judge took his horse from the corral, took a fair sum for his services, and rode off into the sunset.
The youngest son complained that the oldest son received 36 horses (but was entitled to only 71/2 = 35.5 horses). The judge was asked about this, and he faxed the children the following message: "You all received more than you deserved. The eldest received 1/2 of an 'extra' horse, the middle child received 1/3 more, and the youngest, 1/9 of a horse 'extra.'" Apportion the horses according to Adams', Jefferson's, and Webster's plans. Which plan gives the appropriate distribution of horses?
A) Adams' plan and Jefferson's plan
B) Webster's plan and Jefferson's plan
C) None of the plans
D) Adams' plan
E) Adams' plan and Webster's plan
The children decided to call in a very wise judge to help in the distribution of the rancher's estate. The judge arrived with a horse of his own. He put his horse in with the 71 belonging to the estate, and then told each child to pick from among the 72 in the proportions stipulated by the will (but be careful, he warned, not to pick his horse). The first child took thirty six horses, the second child took twenty four, and the third child, eight. The 71 horses were thus divided among the children. The wise judge took his horse from the corral, took a fair sum for his services, and rode off into the sunset.
The youngest son complained that the oldest son received 36 horses (but was entitled to only 71/2 = 35.5 horses). The judge was asked about this, and he faxed the children the following message: "You all received more than you deserved. The eldest received 1/2 of an 'extra' horse, the middle child received 1/3 more, and the youngest, 1/9 of a horse 'extra.'" Apportion the horses according to Adams', Jefferson's, and Webster's plans. Which plan gives the appropriate distribution of horses?
A) Adams' plan and Jefferson's plan
B) Webster's plan and Jefferson's plan
C) None of the plans
D) Adams' plan
E) Adams' plan and Webster's plan

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
11
Apportion the indicated number of representatives to three states, A, B, and C, using Hamilton's plan. Next, use the revised populations to reapportion the representatives. Decide whether the population paradox occurs. 
A) A illustrates population paradox.
B) B and C illustrate population paradox.
C) B illustrates population paradox.
D) C illustrates population paradox.
E) The paradox does not occur.

A) A illustrates population paradox.
B) B and C illustrate population paradox.
C) B illustrates population paradox.
D) C illustrates population paradox.
E) The paradox does not occur.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
12
Use Jefferson's plan. Which state does violate the quota rule? 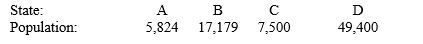 Number of seats:
Number of seats:  200
200
A) C
B) B
C) D
D) A
E) none
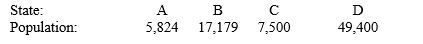 Number of seats:
Number of seats:  200
200
A) C
B) B
C) D
D) A
E) none

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
13
Apportion the indicated number of representatives to two states, A, and B, using Hamilton's plan. Next, recalculate the apportionment using Hamilton's plan for the three states, C and the original states. Decide whether the new states paradox occurs. 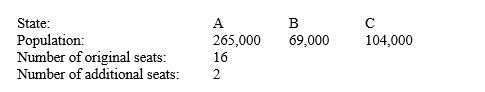
A) B illustrates the new states paradox.
B) C illustrates the new states paradox.
C) A and C illustrate the new states paradox.
D) A illustrates the new states paradox.
E) The paradox does not occur.
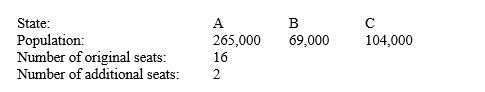
A) B illustrates the new states paradox.
B) C illustrates the new states paradox.
C) A and C illustrate the new states paradox.
D) A illustrates the new states paradox.
E) The paradox does not occur.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
14
Round the given modified quota
3)57
By comparing it first with the arithmetic mean, and then with the geometric mean of the lower and upper quotas.
A) 4; 4
B) 3; 3
C) 0; 1
D) 4; 3
E) 3; 4
3)57
By comparing it first with the arithmetic mean, and then with the geometric mean of the lower and upper quotas.
A) 4; 4
B) 3; 3
C) 0; 1
D) 4; 3
E) 3; 4

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
15
Apportion the indicated number of representatives to two states, A, and B, using Hamilton's plan. Next, recalculate the apportionment using Hamilton's plan for the three states, C and the original states. Decide whether the new states paradox occurs. 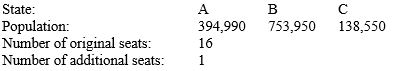
__________ (A illustrates the new states paradox.; B illustrates the new states paradox.; C illustrates the new states paradox.; A and B illustrate the new states paradox.; The paradox does not occur.)
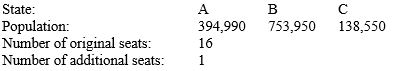
__________ (A illustrates the new states paradox.; B illustrates the new states paradox.; C illustrates the new states paradox.; A and B illustrate the new states paradox.; The paradox does not occur.)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
16
Apportion the indicated number of representatives to two states, A, and B, using Hamilton's plan. Next, recalculate the apportionment using Hamilton's plan for the three states, C and the original states. Decide whether the new states paradox occurs. 
__________ (A illustrates the new states paradox.; B illustrates the new states paradox.; C illustrates the new states paradox.; A and B illustrate the new states paradox.; The paradox does not occur.)

__________ (A illustrates the new states paradox.; B illustrates the new states paradox.; C illustrates the new states paradox.; A and B illustrate the new states paradox.; The paradox does not occur.)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
17
Apportion the indicated number of representatives to three states, A, B, and C, using Hamilton's plan. Next, use the revised populations to reapportion the representatives. Decide whether the population paradox occurs. 
__________ (A illustrates population paradox.; B illustrates population paradox.; C illustrates population paradox.; B and C illustrate population paradox.; The paradox does not occur.)

__________ (A illustrates population paradox.; B illustrates population paradox.; C illustrates population paradox.; B and C illustrate population paradox.; The paradox does not occur.)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
18
A fair apportionment of dividing a leftover piece of cake between two children is to let child #1 cut the cake into two pieces and then to let child #2 pick which piece he or she wants. Consider the following apportionment of dividing the leftover piece of cake among three children. Let the first child cut the cake into two pieces. Then the second child is permitted to cut one of those pieces into two parts. Child #3 can select any of the pieces, followed by child #1 selecting one of the remaining pieces, followed by child #2 who gets the remaining piece. Is this allocation process fair if each child's goal is to maximize the size of his or her own piece of cake?
__________ (Yes, No)
__________ (Yes, No)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose the annual salaries of three people are: 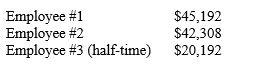 What are their salaries if they are given a 4% raise, and then the result is rounded to the nearest $1,000 using Hamilton's plan with a cap on the total salaries of $113,000?
What are their salaries if they are given a 4% raise, and then the result is rounded to the nearest $1,000 using Hamilton's plan with a cap on the total salaries of $113,000?
A)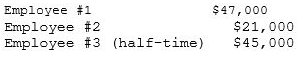
B)
C)
D)
E)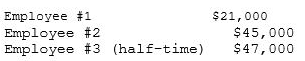
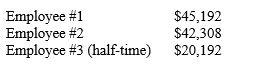 What are their salaries if they are given a 4% raise, and then the result is rounded to the nearest $1,000 using Hamilton's plan with a cap on the total salaries of $113,000?
What are their salaries if they are given a 4% raise, and then the result is rounded to the nearest $1,000 using Hamilton's plan with a cap on the total salaries of $113,000? A)
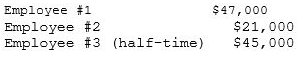
B)

C)

D)

E)
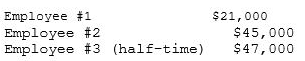

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
20
Use Hamilton's plan to apportion the new seats to the existing states. Then increase the number of seats by one and decide whether the Alabama paradox occurs. Assume that the populations are in thousands. 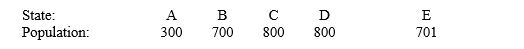 Number of seats:
Number of seats:  81
81
__________ (A illustrates Alabama paradox.; B illustrates Alabama paradox.; C illustrates Alabama paradox.; D illustrates Alabama paradox.; The Alabama paradox does not occur.)
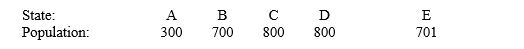 Number of seats:
Number of seats:  81
81
__________ (A illustrates Alabama paradox.; B illustrates Alabama paradox.; C illustrates Alabama paradox.; D illustrates Alabama paradox.; The Alabama paradox does not occur.)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
21
The Adobe School District is hiring a vice principal and has interviewed four candidates: Anna (A), Bono (B), Clark (C), and David (D). The hiring committee has indicated their preferences. 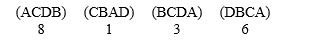 Who is the winner using the plurality method? Answer A, B, C, or D.
Who is the winner using the plurality method? Answer A, B, C, or D.
Do the results of the previous questions violate the irrelevant alternatives criterion? Answer yes or no.
Suppose that Bono drops out of the running before the vote is taken. Who is the winner using the plurality method? Answer A, B, C, or D.
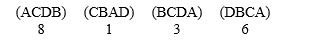 Who is the winner using the plurality method? Answer A, B, C, or D.
Who is the winner using the plurality method? Answer A, B, C, or D.Do the results of the previous questions violate the irrelevant alternatives criterion? Answer yes or no.
Suppose that Bono drops out of the running before the vote is taken. Who is the winner using the plurality method? Answer A, B, C, or D.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
22
A group of fun-loving people have decided to play a practical joke on one of their friends, but they can't decide which friend, Alice (A), Betty (B), or Connie (C). Their preferences are:  Who wins using the Borda count method? Does this violate the Condorcet criterion?
Who wins using the Borda count method? Does this violate the Condorcet criterion?
A) Betty, No
B) Connie, No
C) Alice, Yes
D) Betty, Yes
E) Alice, No
 Who wins using the Borda count method? Does this violate the Condorcet criterion?
Who wins using the Borda count method? Does this violate the Condorcet criterion?
A) Betty, No
B) Connie, No
C) Alice, Yes
D) Betty, Yes
E) Alice, No

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
23
In voting among three candidates, the outcomes are reported as: 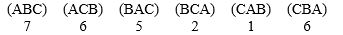 How many voters did rank three candidates in the order of C first, A next, and candidate B last?
How many voters did rank three candidates in the order of C first, A next, and candidate B last?
A) 6
B) 5
C) 7
D) 2
E) 1
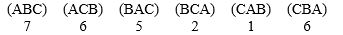 How many voters did rank three candidates in the order of C first, A next, and candidate B last?
How many voters did rank three candidates in the order of C first, A next, and candidate B last?
A) 6
B) 5
C) 7
D) 2
E) 1

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
24
A focus group of 41 people for ABC TV were asked to rank the government spending priorities of education (E), military spending (M), health care (H), immigration (I), and lowering taxes (T). Here are the preferences: 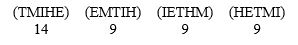
Suppose that the losing issues of immigration, health care, and military spending are removed from the table. Now, who is the winner using the Borda count method?
A) T
B) E
C) No winner.
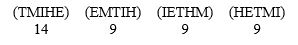
Suppose that the losing issues of immigration, health care, and military spending are removed from the table. Now, who is the winner using the Borda count method?
A) T
B) E
C) No winner.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
25
The seniors at a high school are voting for where to go for their senior trip. They are deciding on Angel Falls (A), Bear Valley (B), Clear Canyon (C), or Dragon Cave (D). The  Determine who wins using the pairwise comparison method.
Determine who wins using the pairwise comparison method.
A) A
B) B
C) C
D) D
E) no winner
 Determine who wins using the pairwise comparison method.
Determine who wins using the pairwise comparison method. A) A
B) B
C) C
D) D
E) no winner

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
26
A focus group of 32 people for ABC TV were asked to rank the government spending priorities of education (E), military spending (M), health care (H), immigration (I), and lowering taxes (T). Here are the preferences:
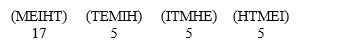
Suppose that the losing issues of immigration, health care, and health care are removed from the table. Now, who is the winner using the Borda count method? AnswerE, H, M, I, or T.
Does the Borda count method violate the irrelevant alternatives criterion? Answer yes or no.
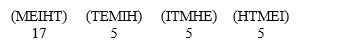
Suppose that the losing issues of immigration, health care, and health care are removed from the table. Now, who is the winner using the Borda count method? AnswerE, H, M, I, or T.
Does the Borda count method violate the irrelevant alternatives criterion? Answer yes or no.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
27
A group of fun-loving people have decided to play a practical joke on one of their friends, but they can't decide which friend, Alice (A), Betty (B), or Connie (C). Their preferences are: 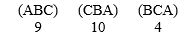
Who wins the election using the Hare method? Answer Alice, Betty, or Connie.
Does this violate the Condorcet criterion? Answer yes or no.
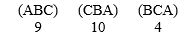
Who wins the election using the Hare method? Answer Alice, Betty, or Connie.
Does this violate the Condorcet criterion? Answer yes or no.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
28
Consider an election with three candidates with the results: 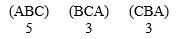 Who wins using the pairwise comparison method?
Who wins using the pairwise comparison method?
A) C
B) A
C) B
D) no winner
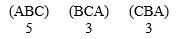 Who wins using the pairwise comparison method?
Who wins using the pairwise comparison method? A) C
B) A
C) B
D) no winner

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
29
The fraternity is electing a national president and there are four candidates: Alberto (A), Bate (B), Carl (C), and Dave (D). The voter preferences are: 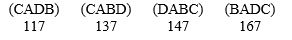
Who wins the election using the Hare method? Answer Alberto, Bate, Carl, or Dave.
Does this violate any of the fairness criteria? Answer Yes. Irrelevant alternative criterion.; Yes. Condition of decisiveness.; Yes. Condorcet criterion.; or No.
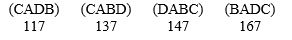
Who wins the election using the Hare method? Answer Alberto, Bate, Carl, or Dave.
Does this violate any of the fairness criteria? Answer Yes. Irrelevant alternative criterion.; Yes. Condition of decisiveness.; Yes. Condorcet criterion.; or No.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
30
Consider an election with three candidates with the results: 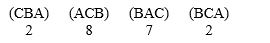 Who wins the election using the Borda count method?
Who wins the election using the Borda count method?
A) A
B) C
C) B
D) C and B tie
E) A and B tie
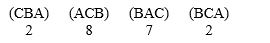 Who wins the election using the Borda count method?
Who wins the election using the Borda count method? A) A
B) C
C) B
D) C and B tie
E) A and B tie

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
31
The Adobe School District is hiring a vice principal and has interviewed four candidates: Alicia (A), Ben (B), Carmelia (C), and Diana (D). The hiring committee has indicated their preferences. 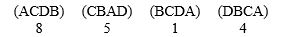 Determine who is the winner using the plurality method. Then suppose that Diana drops out of the running before the vote is taken. Do the results you obtain violate the irrelevant alternatives criterion?
Determine who is the winner using the plurality method. Then suppose that Diana drops out of the running before the vote is taken. Do the results you obtain violate the irrelevant alternatives criterion?
A) Yes
B) No
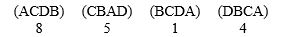 Determine who is the winner using the plurality method. Then suppose that Diana drops out of the running before the vote is taken. Do the results you obtain violate the irrelevant alternatives criterion?
Determine who is the winner using the plurality method. Then suppose that Diana drops out of the running before the vote is taken. Do the results you obtain violate the irrelevant alternatives criterion? A) Yes
B) No

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
32
A focus group of 40 people for ABC TV were asked to rank the government spending priorities of education (E), military spending (M), health care (H), immigration (I), and lowering taxes (T). Here are the preferences: 
Who is the winner using the pairwise comparison method? Answer E, M, H, I, or T.

Who is the winner using the pairwise comparison method? Answer E, M, H, I, or T.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
33
The fraternity is electing a national president and there are four candidates: Alberto (A), Bate (B), Carl (C), and Dave (D). The voter preferences are: 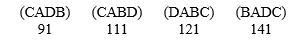 Who wins the election using the Hare method? Does this violate any of the fairness criteria?
Who wins the election using the Hare method? Does this violate any of the fairness criteria?
A) Dave. Yes. Condorcet criterion.
B) Carl. No.
C) Bate. Yes. Condorcet criterion.
D) Carl. Yes. Condorcet criterion.
E) Bate. No.
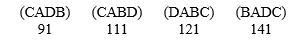 Who wins the election using the Hare method? Does this violate any of the fairness criteria?
Who wins the election using the Hare method? Does this violate any of the fairness criteria? A) Dave. Yes. Condorcet criterion.
B) Carl. No.
C) Bate. Yes. Condorcet criterion.
D) Carl. Yes. Condorcet criterion.
E) Bate. No.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
34
Find the standard divisor (to two decimal places) for the given population and number of representative seats. Population
# seats
140,000
9
A) 14,055.56
B) 17,055.56
C) 16,055
D) 15,555.56
E) 13,056
# seats
140,000
9
A) 14,055.56
B) 17,055.56
C) 16,055
D) 15,555.56
E) 13,056

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
35
Consider an election with three candidates with the results: 
Is there a majority winner? If not, who is the plurality winner? Answer No, B; Yes, C; No, C; No, A; or Yes, B
Who wins using the pairwise comparison method? Answer A, C, or
B.
Is the ordering for the choices for candidates in the previous question transitive? Answer yes or no.

Is there a majority winner? If not, who is the plurality winner? Answer No, B; Yes, C; No, C; No, A; or Yes, B
Who wins using the pairwise comparison method? Answer A, C, or
B.
Is the ordering for the choices for candidates in the previous question transitive? Answer yes or no.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
36
The seniors at a high school are voting for where to go for their senior trip. They are deciding on Apple Valley (A), Bend Canyon (B), Crystal River (C), or Danger Gap (D). The results of the preferences are: 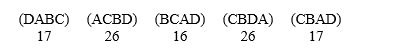 Who wins using the pairwise comparison method? Answer A, B, C, or D.
Who wins using the pairwise comparison method? Answer A, B, C, or D.
Does this violate the Condorcet criterion? Answer yes or no.
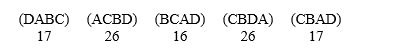 Who wins using the pairwise comparison method? Answer A, B, C, or D.
Who wins using the pairwise comparison method? Answer A, B, C, or D.Does this violate the Condorcet criterion? Answer yes or no.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
37
A group of fun-loving people have decided to play a practical joke on one of their friends, but they can't decide which friend, Alice (A), Betty (B), or Connie (C). Their preferences are: 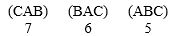 Who wins the election using the Hare method? Does this violate the Condorcet criterion?
Who wins the election using the Hare method? Does this violate the Condorcet criterion?
A) Betty, Yes
B) Alice, Yes
C) Connie, No
D) Betty, No
E) Connie, Yes
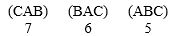 Who wins the election using the Hare method? Does this violate the Condorcet criterion?
Who wins the election using the Hare method? Does this violate the Condorcet criterion? A) Betty, Yes
B) Alice, Yes
C) Connie, No
D) Betty, No
E) Connie, Yes

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
38
If there are 190 voters and 4 candidates, how many total points would there be in a Borda count?
A) 1,890
B) 1,900
C) 1,860
D) 1,920
E) 1,930
A) 1,890
B) 1,900
C) 1,860
D) 1,920
E) 1,930

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
39
Consider an election with three candidates with the results: 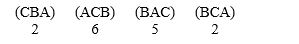
Is there a majority winner? If not, who is the plurality winner? Answer No, B; Yes, A; No, A; No, C; or Yes,
B.
Who wins the election using the Borda count method? Answer B; A; C and B tie; C; or A and B tie.
Who wins if they first eliminate the one with the most last-place votes and then have a runoff between the other two? Answer B; A; C and B tie; C; or A and B tie.
Could the two voters with preference (BCA) change the outcome of the election in previous question if they voted insincerely and pretended to have the preference (BAC)? Answer yes or no.
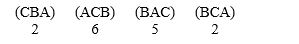
Is there a majority winner? If not, who is the plurality winner? Answer No, B; Yes, A; No, A; No, C; or Yes,
B.
Who wins the election using the Borda count method? Answer B; A; C and B tie; C; or A and B tie.
Who wins if they first eliminate the one with the most last-place votes and then have a runoff between the other two? Answer B; A; C and B tie; C; or A and B tie.
Could the two voters with preference (BCA) change the outcome of the election in previous question if they voted insincerely and pretended to have the preference (BAC)? Answer yes or no.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
40
In voting among four candidates, the outcomes are reported as: 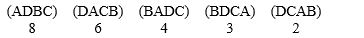 How many voters did rank three candidates in the order of A first, D second, B third, and candidate C last?
How many voters did rank three candidates in the order of A first, D second, B third, and candidate C last?
A) 4
B) 8
C) 3
D) 2
E) 6
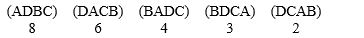 How many voters did rank three candidates in the order of A first, D second, B third, and candidate C last?
How many voters did rank three candidates in the order of A first, D second, B third, and candidate C last?
A) 4
B) 8
C) 3
D) 2
E) 6

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose your college transcripts show the distribution of grades: 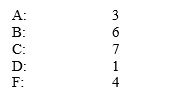
Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
Which voting method describes how you answered previous question? Answer majority method, plurality method, borda count method, hare method, pairwise comparison method, tournament method, or approval method.
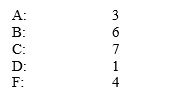
Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
Which voting method describes how you answered previous question? Answer majority method, plurality method, borda count method, hare method, pairwise comparison method, tournament method, or approval method.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the situation. A political party holds a national convention with 1,100 delegates. At the convention, five persons (which we will call A, B, C, D, and E) have been nominated as the party's presidential candidate. After the speeches and hoopla, the delegates are asked to rank all five candidates according to his or her choice. However, before the vote, caucuses have narrowed the choices down to six different possibilities. The results of the first ballot are shown (choices, followed by the number of votes): 
How many possible rankings are there?

How many possible rankings are there?

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the following situation. A political party holds a national convention with 1,100 delegates. At the convention, five persons (which we will call A, B, C, D, and E) have been nominated as the party's presidential candidate. After the speeches and hoopla, the delegates are asked to rank all five candidates according to his or her choice. However, before the vote, caucuses have narrowed the choices down to six different possibilities. The results of the first ballot are shown (choices, followed by the number of votes):  Who would win in a runoff election using the principle of eliminating the candidate with the fewest first-place votes?
Who would win in a runoff election using the principle of eliminating the candidate with the fewest first-place votes?
A) B
B) C
C) A
D) E
E) D
 Who would win in a runoff election using the principle of eliminating the candidate with the fewest first-place votes?
Who would win in a runoff election using the principle of eliminating the candidate with the fewest first-place votes?
A) B
B) C
C) A
D) E
E) D

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose your college transcripts show the distribution of grades: 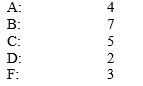 Suppose that all of these grades are in three-unit classes.
Suppose that all of these grades are in three-unit classes.
Which grade is the most common?
A) C
B) B
C) A
D) F
E) D
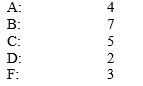 Suppose that all of these grades are in three-unit classes.
Suppose that all of these grades are in three-unit classes.Which grade is the most common?
A) C
B) B
C) A
D) F
E) D

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
45
In voting among three candidates, the outcomes are reported as: 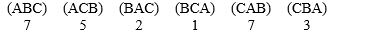 Determine the winner, if any, using Hare method.
Determine the winner, if any, using Hare method.
A) A
B) C
C) B
D) none of them
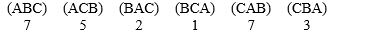 Determine the winner, if any, using Hare method.
Determine the winner, if any, using Hare method.
A) A
B) C
C) B
D) none of them

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the situation. A political party holds a national convention with 1,100 delegates. At the convention, five persons (which we will call A, B, C, D, and E) have been nominated as the party's presidential candidate. After the speeches and hoopla, the delegates are asked to rank all five candidates according to his or her choice. However, before the vote, caucuses have narrowed the choices down to six different possibilities. The results of the first ballot are shown (choices, followed by the number of votes):  How many possible rankings are there?
How many possible rankings are there?
A) 240
B) 720
C) 120
D) 110
E) 24
 How many possible rankings are there?
How many possible rankings are there?
A) 240
B) 720
C) 120
D) 110
E) 24

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
47
In voting among four candidates, the outcomes are reported as: 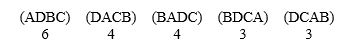
What does the notation (BADC) mean?
"(BADC)" means that the voter ranks three candidates in the order of __________ first, __________ second, __________ third, and candidate __________ last.
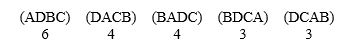
What does the notation (BADC) mean?
"(BADC)" means that the voter ranks three candidates in the order of __________ first, __________ second, __________ third, and candidate __________ last.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
48
The race for the governor of Vermont, suppose the state vote was as follows: 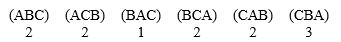
Was there a majority winner in this election, and if so, who was it?
A) Hardy Macia
B) Phil Stannard
C) Joel Williams
D) Ruth Dwyer
E) Marilyn Christian
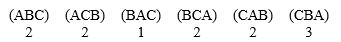
Was there a majority winner in this election, and if so, who was it?
A) Hardy Macia
B) Phil Stannard
C) Joel Williams
D) Ruth Dwyer
E) Marilyn Christian

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
49
If there are 10 voters and 5 candidates, how many total points would there be in a Borda count?
__________ points
__________ points

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
50
In the race for the governor of Vermont, the state vote was as follows: 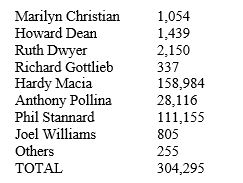
Was there a majority winner in this election, and if so, who was it?

Was there a majority winner in this election, and if so, who was it?

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
51
Twelve people serve on a board and are considering three alternatives A, B, and C. Here are the choices followed by vote: 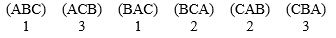 Determine the winner using Hare method.
Determine the winner using Hare method.
Answer A, B, C, or none of them.
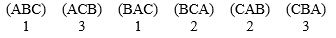 Determine the winner using Hare method.
Determine the winner using Hare method.Answer A, B, C, or none of them.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
52
In voting among three candidates, the outcomes are reported as: 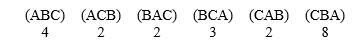 Determine the winner, if any, using Hare method.
Determine the winner, if any, using Hare method.
Answer A, B, C, or none of them.
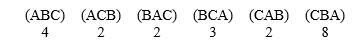 Determine the winner, if any, using Hare method.
Determine the winner, if any, using Hare method.Answer A, B, C, or none of them.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck


