Deck 15: Topics in Vector Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/149
Play
Full screen (f)
Deck 15: Topics in Vector Calculus
1
Use Stokes' Theorem to evaluate C 28z dx - 14x dy + 14x dz where C is the intersection of the cylinder x2 + y2 = 1 and the plane z = y + 1.
A)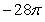
B)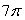
C) 0
D)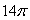
E)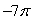
A)
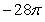
B)
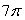
C) 0
D)
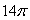
E)
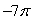
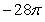
2
Use Stokes' Theorem to evaluate 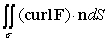 where F(x, y, z) = 5x j and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 8 for which z 0.
where F(x, y, z) = 5x j and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 8 for which z 0.
A) 5
B) 0
C) 12
D)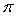
E)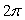
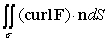 where F(x, y, z) = 5x j and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 8 for which z 0.
where F(x, y, z) = 5x j and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 8 for which z 0.A) 5
B) 0
C) 12
D)
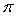
E)
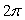
0
3
Use Stokes' Theorem to evaluate C 2(x + y)dx + 2(2x - 3)dy + 2(y + z)dz over the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0), and (0, 0, 6) traversed in a counterclockwise manner.
A) 2
B) 12
C) 0
D) 24
E) 18
A) 2
B) 12
C) 0
D) 24
E) 18
24
4
Use Stokes' Theorem to evaluate C 11z dx + 11x dy + 11y dz over the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1) traversed in a counterclockwise manner.
A) 16.5
B) 11
C) 22
D) 44
E) 1
A) 16.5
B) 11
C) 22
D) 44
E) 1

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
5
Find the outward flux of the vector field 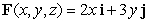 across the sphere
across the sphere 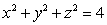 .
.
A)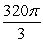
B) 0
C)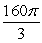
D)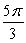
E)
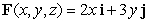 across the sphere
across the sphere 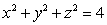 .
.A)
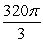
B) 0
C)
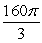
D)
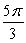
E)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
6
Verify Stokes' Theorem if is the portion of the sphere x2 + y2 + z2 = 1 for which z 0 and F(x, y, z) = (2x - y)i - yz2 j - y2z k.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
7
Use Stokes' Theorem to evaluate C -4yz dx + 4xz dy + 4xy dz where C is the circle x2 + y2 = 2, z = 1.
A) 4
B) 16
C)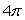
D)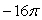
E)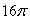
A) 4
B) 16
C)
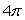
D)
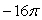
E)
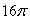

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
8
Use Stokes' Theorem to evaluate C -21 dx + 21x dy + 7z dz over the circle x2 + y2 = 1, z = 1 traversed counterclockwise.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
9
Use Stokes' Theorem to evaluate 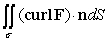 where F(x, y, z) = 11(z - y)i + 11(z2 + x)j + 11(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
where F(x, y, z) = 11(z - y)i + 11(z2 + x)j + 11(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
A)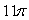
B)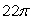
C)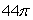
D)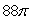
E)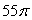
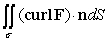 where F(x, y, z) = 11(z - y)i + 11(z2 + x)j + 11(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
where F(x, y, z) = 11(z - y)i + 11(z2 + x)j + 11(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.A)
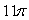
B)
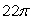
C)
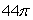
D)
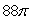
E)
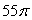

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
10
Use Stokes' Theorem to evaluate C 3(4x - 2y)dx - 3yz2dy - 3y2z dz where C is the circular region enclosed by x2 + y2 = 4, z = 2.
A) 3
B) 24
C)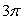
D)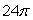
E) 0
A) 3
B) 24
C)
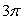
D)
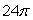
E) 0

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
11
Use Stokes' Theorem to evaluate C 30y2dx + 30x2dy - 30(x + z)dz where C is a triangle in the xy-plane with vertices (0, 0, 0), (1, 0, 0), and (1, 1, 0) with a counterclockwise orientation looking down the positive z axis.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
12
Use Stokes' Theorem to evaluate C 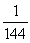 (x + y)dx +
(x + y)dx + 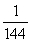 (2x - 3)dy +
(2x - 3)dy + 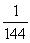 (y + z)dz over the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0), and (0, 0, 6) traversed in a counterclockwise manner.
(y + z)dz over the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0), and (0, 0, 6) traversed in a counterclockwise manner.
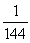 (x + y)dx +
(x + y)dx + 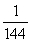 (2x - 3)dy +
(2x - 3)dy + 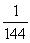 (y + z)dz over the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0), and (0, 0, 6) traversed in a counterclockwise manner.
(y + z)dz over the boundary of the triangle with vertices (2, 0, 0), (0, 3, 0), and (0, 0, 6) traversed in a counterclockwise manner. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
13
Use Stokes' Theorem to evaluate 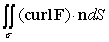 where F(x, y, z) = 3y i and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0.
where F(x, y, z) = 3y i and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0.
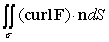 where F(x, y, z) = 3y i and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0.
where F(x, y, z) = 3y i and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
14
Use Stokes' Theorem to evaluate 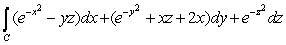 over the circle x2 + y2 = 16, z = 4.
over the circle x2 + y2 = 16, z = 4.
A) 0
B) 64
C) -64
D)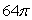
E)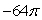
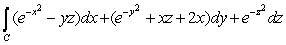 over the circle x2 + y2 = 16, z = 4.
over the circle x2 + y2 = 16, z = 4.A) 0
B) 64
C) -64
D)
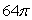
E)
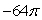

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
15
Use Stokes' Theorem to evaluate C 3sin z dx - 3cos x dy + 3sin y dz over the rectangle
0 x , 0 y 1, and z = 2 traversed in a counterclockwise manner.
0 x , 0 y 1, and z = 2 traversed in a counterclockwise manner.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
16
Use Stokes' Theorem to evaluate 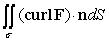 where F(x, y, z) =
where F(x, y, z) = 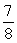 (z - y)i +
(z - y)i + 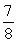 (z2 + x)j +
(z2 + x)j + 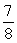 (x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
A)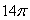
B)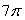
C) 0
D)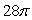
E)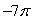
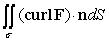 where F(x, y, z) =
where F(x, y, z) = 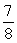 (z - y)i +
(z - y)i + 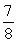 (z2 + x)j +
(z2 + x)j + 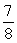 (x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.
(x2 - y2)k and is that portion of the sphere x2 + y2 + z2 = 4 for which z 0.A)
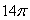
B)
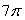
C) 0
D)
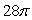
E)
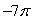

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
17
Use Stokes' Theorem to evaluate C 8z dx - 4x dy + 4x dz where C is the intersection of the cylinder x2 + y2 = 1 and the plane z = y + 1.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
18
Use Stokes' Theorem to evaluate 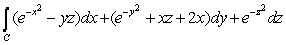 over the circle x2 + y2 = 1, z = 1.
over the circle x2 + y2 = 1, z = 1.
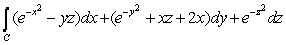 over the circle x2 + y2 = 1, z = 1.
over the circle x2 + y2 = 1, z = 1.
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
19
Use Stokes' Theorem to evaluate C 3(z - y)dx + 3(x - z)dy + 3(y - x)dz where C is the boundary, in the xy-plane, of the surface given by z = 4 - (x2 + y2), z 0.
A)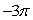
B)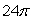
C) 0
D)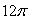
E)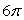
A)
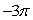
B)
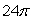
C) 0
D)
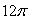
E)
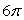

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
20
Use Stokes' Theorem to evaluate 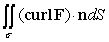 where F(x, y, z) = 8y k and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0.
where F(x, y, z) = 8y k and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0.
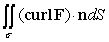 where F(x, y, z) = 8y k and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0.
where F(x, y, z) = 8y k and is that portion of the ellipsoid 4x2 + 4y2 + z2 = 4 for which z 0. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
21
F (x, y, z) = 5xyz i + 5xyz j + 5xyz k. Find the outward flux of the vector field F across the unit cube in the first octant and including the origin as a vertex.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
22
Use the divergence theorem to evaluate 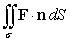 where F(x, y, z) = 2e x i - 2ye x j + 6z k, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.
where F(x, y, z) = 2e x i - 2ye x j + 6z k, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.
A)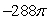
B)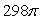
C)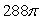
D)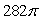
E)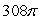
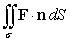 where F(x, y, z) = 2e x i - 2ye x j + 6z k, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.
where F(x, y, z) = 2e x i - 2ye x j + 6z k, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.A)
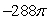
B)
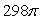
C)
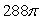
D)
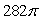
E)
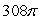

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
23
Let 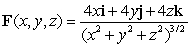 and let be a closed, orientable surface that surrounds the origin. Then the flux =
and let be a closed, orientable surface that surrounds the origin. Then the flux =
A) 7
B) 0
C) 100
D) 16
E)
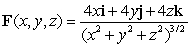 and let be a closed, orientable surface that surrounds the origin. Then the flux =
and let be a closed, orientable surface that surrounds the origin. Then the flux =A) 7
B) 0
C) 100
D) 16
E)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
24
Use the divergence theorem to evaluate 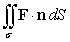 where
where 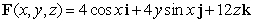 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 9.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 9.
A)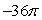
B)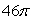
C)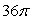
D)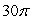
E)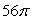
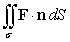 where
where 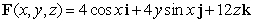 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 9.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 9.A)
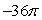
B)
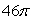
C)
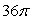
D)
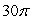
E)
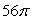

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
25
Use the divergence theorem to evaluate 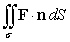 where F(x, y, z) = 11yz i + 11xy j + 11xz k, n is the outer unit normal to , and is the surface enclosed by the cylinder x2 + z2 = 1 and the planes y = -1 and y = 1.
where F(x, y, z) = 11yz i + 11xy j + 11xz k, n is the outer unit normal to , and is the surface enclosed by the cylinder x2 + z2 = 1 and the planes y = -1 and y = 1.
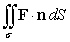 where F(x, y, z) = 11yz i + 11xy j + 11xz k, n is the outer unit normal to , and is the surface enclosed by the cylinder x2 + z2 = 1 and the planes y = -1 and y = 1.
where F(x, y, z) = 11yz i + 11xy j + 11xz k, n is the outer unit normal to , and is the surface enclosed by the cylinder x2 + z2 = 1 and the planes y = -1 and y = 1. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
26
Use the divergence theorem to evaluate 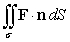 where F(x, y, z) = 2y2x i + 2yz2 j + 2x2y2 k, n is the outer unit normal to , and is the sphere x2 + y2 + z2 = 4.
where F(x, y, z) = 2y2x i + 2yz2 j + 2x2y2 k, n is the outer unit normal to , and is the sphere x2 + y2 + z2 = 4.
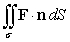 where F(x, y, z) = 2y2x i + 2yz2 j + 2x2y2 k, n is the outer unit normal to , and is the sphere x2 + y2 + z2 = 4.
where F(x, y, z) = 2y2x i + 2yz2 j + 2x2y2 k, n is the outer unit normal to , and is the sphere x2 + y2 + z2 = 4. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
27
Find the outward flux of the vector field 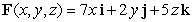 across the sphere
across the sphere 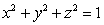 .
.
A)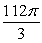
B)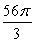
C) 0
D)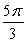
E)
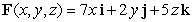 across the sphere
across the sphere 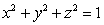 .
.A)
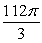
B)
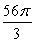
C) 0
D)
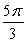
E)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
28
Use the divergence theorem to evaluate 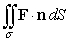 where F(x, y, z) = (x3 + 3xy2)i + z3 k, n is the outer unit normal to , and is the surface of the sphere of radius a centered at the origin.
where F(x, y, z) = (x3 + 3xy2)i + z3 k, n is the outer unit normal to , and is the surface of the sphere of radius a centered at the origin.
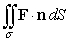 where F(x, y, z) = (x3 + 3xy2)i + z3 k, n is the outer unit normal to , and is the surface of the sphere of radius a centered at the origin.
where F(x, y, z) = (x3 + 3xy2)i + z3 k, n is the outer unit normal to , and is the surface of the sphere of radius a centered at the origin. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
29
Use the divergence theorem to evaluate 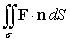 where
where 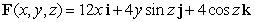 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.
A)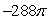
B)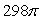
C)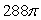
D)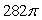
E)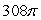
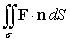 where
where 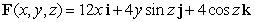 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 36.A)
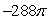
B)
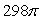
C)
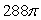
D)
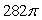
E)
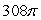

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
30
F (x, y, z) = 8x3 i + 16y2 j + 24z2 k. Find the outward flux of the vector field F across the unit cube in the first octant and including the origin as a vertex.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
31
Find the outward flux of F(x, y, z) = 4x i + 4y j + 4(z - 2)k across the rectangular box with vertices (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (3, 0, 0), (3, 1, 0), (3, 0, 1), and (3, 1, 1).
A) 12
B) 36
C) 0
D) 1
E) 4
A) 12
B) 36
C) 0
D) 1
E) 4

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
32
Let 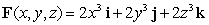 Find the outward flux of the vector field F across the surface of the region bounded above by the sphere by x2 + y2 + z2 = 4 and below by the plane z = 0.
Find the outward flux of the vector field F across the surface of the region bounded above by the sphere by x2 + y2 + z2 = 4 and below by the plane z = 0.
A)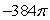
B)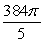
C)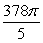
D)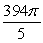
E)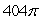
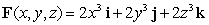 Find the outward flux of the vector field F across the surface of the region bounded above by the sphere by x2 + y2 + z2 = 4 and below by the plane z = 0.
Find the outward flux of the vector field F across the surface of the region bounded above by the sphere by x2 + y2 + z2 = 4 and below by the plane z = 0.A)
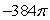
B)
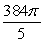
C)
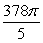
D)
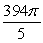
E)
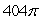

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
33
Use the divergence theorem to evaluate 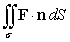 where
where 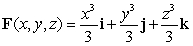 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 49.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 49.
A)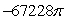
B)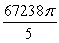
C)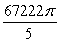
D)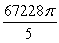
E)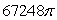
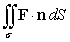 where
where 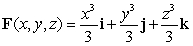 , n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 49.
, n is the outer unit normal to , and is the surface of the sphere by x2 + y2 + z2 = 49.A)
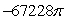
B)
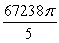
C)
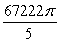
D)
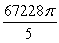
E)
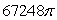

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
34
Find the outward flux of F(x, y, z) = 5(x - 1)i + 5(y - 3)j + 5z k across the rectangular box with vertices (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (4, 0, 0), (4, 1, 0), (4, 0, 1), and (4, 1, 1).
A) 15
B) 60
C) 0
D) 1
E) 6
A) 15
B) 60
C) 0
D) 1
E) 6

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
35
F (x, y, z) = 12xyz i + 12xyz j + 12xyz k. Find the outward flux of the vector field F across the cube with vertices (0, 0, 0), (0, 0, 2), (0, 2, 2), (2, 2, 2), (0, 2, 0), (2, 0, 0), (2, 2, 0), and (2, 0, 2).

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
36
Determine whether the flow field F(x, y, z) = 10x2 i + 10y2 j + 10x2 k is free of all sources and sinks. If it is not, find the location of all sources and sinks.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
37
Let F(x, y, z) = 8x2 i + 6y j + 3z k . Find the outward flux of the vector field F across the unit cube in the first octant and including the origin as a vertex.
A) 17
B) 18
C) 16
D) 27
E) 37
A) 17
B) 18
C) 16
D) 27
E) 37

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
38
Find the outward flux of F(x, y, z) = 5x i + (y + 3)j + 8z2 k across the unit cube in the first octant that has a vertex at the origin.
A) 1
B) 0
C) 8
D) 9
E) 10
A) 1
B) 0
C) 8
D) 9
E) 10

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
39
Use the divergence theorem to evaluate 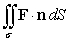 where F(x, y, z) = 4x2 i + 4y2 j + 4z2 k, n is the outer unit normal to , and is the surface of the cube enclosed by the planes 0 x 1, 0 y 1, and 0 z 1.
where F(x, y, z) = 4x2 i + 4y2 j + 4z2 k, n is the outer unit normal to , and is the surface of the cube enclosed by the planes 0 x 1, 0 y 1, and 0 z 1.
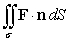 where F(x, y, z) = 4x2 i + 4y2 j + 4z2 k, n is the outer unit normal to , and is the surface of the cube enclosed by the planes 0 x 1, 0 y 1, and 0 z 1.
where F(x, y, z) = 4x2 i + 4y2 j + 4z2 k, n is the outer unit normal to , and is the surface of the cube enclosed by the planes 0 x 1, 0 y 1, and 0 z 1. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether the flow field F(x, y, z) = 5x3 i + 5y3 j + 5z3 k is free of all sources and sinks. If it is not, find the location of all sources and sinks.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate 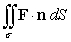 where F(x, y, z) = 2 i - z j + y k and is that portion of the paraboloid x = y2 + z2 between x = 0 and x = 4. The surface is oriented by forward unit normals.
where F(x, y, z) = 2 i - z j + y k and is that portion of the paraboloid x = y2 + z2 between x = 0 and x = 4. The surface is oriented by forward unit normals.
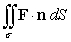 where F(x, y, z) = 2 i - z j + y k and is that portion of the paraboloid x = y2 + z2 between x = 0 and x = 4. The surface is oriented by forward unit normals.
where F(x, y, z) = 2 i - z j + y k and is that portion of the paraboloid x = y2 + z2 between x = 0 and x = 4. The surface is oriented by forward unit normals. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate 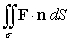 where F(x, y, z) = 2x i + 2y j + 4z k and is that portion of the surface z = 4 - x2 - y2 above the xy-plane oriented by upward unit normals.
where F(x, y, z) = 2x i + 2y j + 4z k and is that portion of the surface z = 4 - x2 - y2 above the xy-plane oriented by upward unit normals.
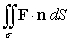 where F(x, y, z) = 2x i + 2y j + 4z k and is that portion of the surface z = 4 - x2 - y2 above the xy-plane oriented by upward unit normals.
where F(x, y, z) = 2x i + 2y j + 4z k and is that portion of the surface z = 4 - x2 - y2 above the xy-plane oriented by upward unit normals. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate 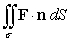 where F(x, y, z) = -x i - 2x j + (z - 1)k and is the surface enclosed by that portion of the paraboloid z = 4 - y2 which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals.
where F(x, y, z) = -x i - 2x j + (z - 1)k and is the surface enclosed by that portion of the paraboloid z = 4 - y2 which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals.
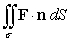 where F(x, y, z) = -x i - 2x j + (z - 1)k and is the surface enclosed by that portion of the paraboloid z = 4 - y2 which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals.
where F(x, y, z) = -x i - 2x j + (z - 1)k and is the surface enclosed by that portion of the paraboloid z = 4 - y2 which lies in the first octant and is bounded by the coordinate planes and the plane y = x. The surface is oriented by upward unit normals. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
44
If F(x, y, z) = 3y j + 3z k, the magnitude of the flux through the portion of the surface that lies right of the yz-plane, where is defined by x = 1 - y2 - z2, is
A)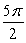
B)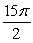
C) 3
D) 0
E)
A)
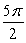
B)
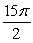
C) 3
D) 0
E)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
45
Find the surface area of (x - 7)2 + (y + 1)2 + (z - 4)2 = 4 that lies below z = 6.
A) 8
B) 32
C) 16
D) 64
E) 128
A) 8
B) 32
C) 16
D) 64
E) 128

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate 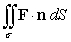 where F(x, y, z) = 2y i + 2z j + 2y k and is that portion of the cone
where F(x, y, z) = 2y i + 2z j + 2y k and is that portion of the cone 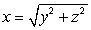 which lies in the first octant between x = 1 and x = 3. The surface is oriented by forward unit normals.
which lies in the first octant between x = 1 and x = 3. The surface is oriented by forward unit normals.
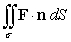 where F(x, y, z) = 2y i + 2z j + 2y k and is that portion of the cone
where F(x, y, z) = 2y i + 2z j + 2y k and is that portion of the cone 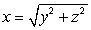 which lies in the first octant between x = 1 and x = 3. The surface is oriented by forward unit normals.
which lies in the first octant between x = 1 and x = 3. The surface is oriented by forward unit normals. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate 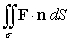 where F(x, y, z) = 18 i - 2z j + 2y k and is that portion of the paraboloid x = 4 - y2 - z2 to the right of x = 0 oriented by forward unit normals.
where F(x, y, z) = 18 i - 2z j + 2y k and is that portion of the paraboloid x = 4 - y2 - z2 to the right of x = 0 oriented by forward unit normals.
A)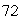
B)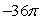
C) 0
D)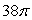
E)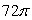
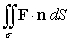 where F(x, y, z) = 18 i - 2z j + 2y k and is that portion of the paraboloid x = 4 - y2 - z2 to the right of x = 0 oriented by forward unit normals.
where F(x, y, z) = 18 i - 2z j + 2y k and is that portion of the paraboloid x = 4 - y2 - z2 to the right of x = 0 oriented by forward unit normals.A)
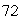
B)
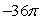
C) 0
D)
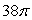
E)
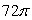

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate 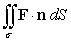 where F(x, y, z) = 9y i - 9x j - 36z2 k and is that portion of the cone
where F(x, y, z) = 9y i - 9x j - 36z2 k and is that portion of the cone 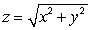 which lies above the square in the xy-plane with vertices (0, 0), (1, 0), (1, 1), and (0, 1), and oriented by downward unit normals.
which lies above the square in the xy-plane with vertices (0, 0), (1, 0), (1, 1), and (0, 1), and oriented by downward unit normals.
A) 72
B) 18
C) 0
D) 24
E) 45
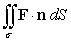 where F(x, y, z) = 9y i - 9x j - 36z2 k and is that portion of the cone
where F(x, y, z) = 9y i - 9x j - 36z2 k and is that portion of the cone 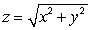 which lies above the square in the xy-plane with vertices (0, 0), (1, 0), (1, 1), and (0, 1), and oriented by downward unit normals.
which lies above the square in the xy-plane with vertices (0, 0), (1, 0), (1, 1), and (0, 1), and oriented by downward unit normals.A) 72
B) 18
C) 0
D) 24
E) 45

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
49
Find the flux of the vector field F(x, y, z) = 5z k across the sphere 5x2 + 5y2 + 5z2 = 20 oriented outward.
A)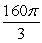
B)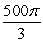
C) 0
D)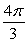
E)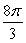
A)
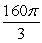
B)
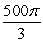
C) 0
D)
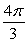
E)
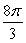

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
50
If F(x, y, z) = 7y j + 7z k, the magnitude of the flux through the portion of the surface that lies in front of the xz-plane, where is defined by y = 1 - x2 - z2, is
A)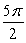
B)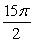
C) 7
D) 0
E)
A)
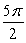
B)
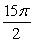
C) 7
D) 0
E)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate 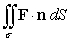 where F(x, y, z) = 4y i + 8x j + 4xy k and is that portion of the cylinder x2 + y2 = 9 in the first octant between z = 1 and z = 4. The surface is oriented by right unit normals.
where F(x, y, z) = 4y i + 8x j + 4xy k and is that portion of the cylinder x2 + y2 = 9 in the first octant between z = 1 and z = 4. The surface is oriented by right unit normals.
A) 0
B) 4
C) 162
D) 8
E) -32
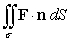 where F(x, y, z) = 4y i + 8x j + 4xy k and is that portion of the cylinder x2 + y2 = 9 in the first octant between z = 1 and z = 4. The surface is oriented by right unit normals.
where F(x, y, z) = 4y i + 8x j + 4xy k and is that portion of the cylinder x2 + y2 = 9 in the first octant between z = 1 and z = 4. The surface is oriented by right unit normals.A) 0
B) 4
C) 162
D) 8
E) -32

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate 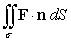 where F(x, y, z) = 4x i + 4y j + 4z k and is that portion of the plane 2x + 3y + 4z = 12 which lies in the first octant and is oriented by upward unit normals.
where F(x, y, z) = 4x i + 4y j + 4z k and is that portion of the plane 2x + 3y + 4z = 12 which lies in the first octant and is oriented by upward unit normals.
A) 144
B) 16
C) 36
D) 72
E) 0
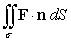 where F(x, y, z) = 4x i + 4y j + 4z k and is that portion of the plane 2x + 3y + 4z = 12 which lies in the first octant and is oriented by upward unit normals.
where F(x, y, z) = 4x i + 4y j + 4z k and is that portion of the plane 2x + 3y + 4z = 12 which lies in the first octant and is oriented by upward unit normals.A) 144
B) 16
C) 36
D) 72
E) 0

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
53
Find the surface area of (x - 1)2 + (y + 1)2 + (z - 4)2 = 4 that lies below z = 4.
A) 8
B) 16
C) 32
D) 64
E) 128
A) 8
B) 16
C) 32
D) 64
E) 128

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
54
Evaluate 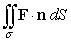 where F(x, y, z) = 12x i + 24j + 24x2 k and is that portion of the paraboloid z = x2 + y2 which lies above the xy-plane enclosed by the parabolas y = 1 - x2 and y = x2 - 1. The surface is oriented by downward unit normals.
where F(x, y, z) = 12x i + 24j + 24x2 k and is that portion of the paraboloid z = x2 + y2 which lies above the xy-plane enclosed by the parabolas y = 1 - x2 and y = x2 - 1. The surface is oriented by downward unit normals.
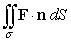 where F(x, y, z) = 12x i + 24j + 24x2 k and is that portion of the paraboloid z = x2 + y2 which lies above the xy-plane enclosed by the parabolas y = 1 - x2 and y = x2 - 1. The surface is oriented by downward unit normals.
where F(x, y, z) = 12x i + 24j + 24x2 k and is that portion of the paraboloid z = x2 + y2 which lies above the xy-plane enclosed by the parabolas y = 1 - x2 and y = x2 - 1. The surface is oriented by downward unit normals. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
55
Let F(x, y, z) = 3y i. The flux outward between the planes z = 0 and z = 2 is
A) 0
B)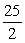
C) 9
D) 3
E)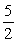
A) 0
B)
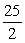
C) 9
D) 3
E)
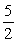

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate 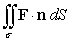 where F(x, y, z) = 3x i + 3y j - 6z k and is that portion of the sphere x2 + y2 + z2 = 9 which lies above the xy-plane and is oriented by upward unit normals.
where F(x, y, z) = 3x i + 3y j - 6z k and is that portion of the sphere x2 + y2 + z2 = 9 which lies above the xy-plane and is oriented by upward unit normals.
A) 12
B) 12
C) 9
D) 0
E) 6
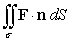 where F(x, y, z) = 3x i + 3y j - 6z k and is that portion of the sphere x2 + y2 + z2 = 9 which lies above the xy-plane and is oriented by upward unit normals.
where F(x, y, z) = 3x i + 3y j - 6z k and is that portion of the sphere x2 + y2 + z2 = 9 which lies above the xy-plane and is oriented by upward unit normals.A) 12
B) 12
C) 9
D) 0
E) 6

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
57
Let F(x, y, z) = 10x i + 10y j + 10z k and be the portion of the surface z = 5 - x2 - y2 that lies above the xy-plane. Find the magnitude of the flux of the vector field across .
A)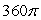
B)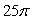
C)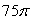
D) 0
E)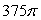
A)
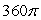
B)
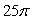
C)
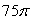
D) 0
E)
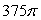

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
58
Find the flux of the vector field F(x, y, z) = 3z k across the sphere x2 + y2 + z2 = 9 oriented outward.
A)
B) 3
C) 0
D) 108
E)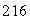
A)
B) 3
C) 0
D) 108
E)
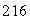

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
59
Find the surface area of the cone 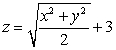 that lies between the planes z = 6 and z = 7.
that lies between the planes z = 6 and z = 7.
A) 7
B)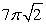
C) 8
D)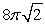
E)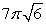
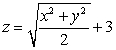 that lies between the planes z = 6 and z = 7.
that lies between the planes z = 6 and z = 7.A) 7
B)
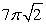
C) 8
D)
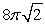
E)
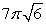

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
60
F(x, y, z) = 4xyz i + 4xyz j + 4xyz k. Find the outward flux of the vector field F across the sphere x2 + y2 + z2 = 25.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the surface integral 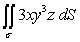 , where is the portion of the cone r(u, v) = u cos v i + u sin v j + u k for which 1 u 2,
, where is the portion of the cone r(u, v) = u cos v i + u sin v j + u k for which 1 u 2, 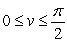 .
.
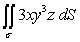 , where is the portion of the cone r(u, v) = u cos v i + u sin v j + u k for which 1 u 2,
, where is the portion of the cone r(u, v) = u cos v i + u sin v j + u k for which 1 u 2, 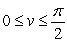 .
. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the surface integral 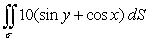 where is that portion of the plane x + y + z = 1 which lies in the first octant.
where is that portion of the plane x + y + z = 1 which lies in the first octant.
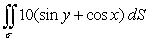 where is that portion of the plane x + y + z = 1 which lies in the first octant.
where is that portion of the plane x + y + z = 1 which lies in the first octant. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the surface integral 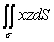 where
where 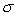 is the part of the plane
is the part of the plane 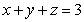 in the first octant.
in the first octant.
A) 3
B) 192
C)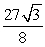
D) 400
E) 800
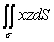 where
where 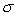 is the part of the plane
is the part of the plane 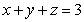 in the first octant.
in the first octant.A) 3
B) 192
C)
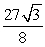
D) 400
E) 800

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the surface integral 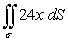 where is the surface enclosed by y = x2, 0 x 2, and -1 z 2.
where is the surface enclosed by y = x2, 0 x 2, and -1 z 2.
A)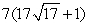
B)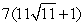
C)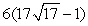
D)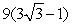
E) 0
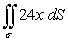 where is the surface enclosed by y = x2, 0 x 2, and -1 z 2.
where is the surface enclosed by y = x2, 0 x 2, and -1 z 2.A)
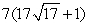
B)
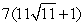
C)
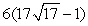
D)
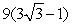
E) 0

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate the surface integral 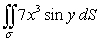 where is the surface enclosed by z = x3, 0 x 2, and 0 y .
where is the surface enclosed by z = x3, 0 x 2, and 0 y .
A)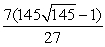
B)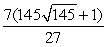
C)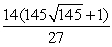
D) 0
E)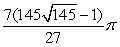
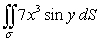 where is the surface enclosed by z = x3, 0 x 2, and 0 y .
where is the surface enclosed by z = x3, 0 x 2, and 0 y .A)
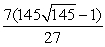
B)
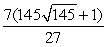
C)
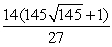
D) 0
E)
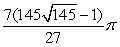

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the surface integral 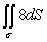 over the sphere x2 + y2 + z2 = 25.
over the sphere x2 + y2 + z2 = 25.
A) 8
B) 800
C)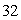
D) 400
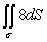 over the sphere x2 + y2 + z2 = 25.
over the sphere x2 + y2 + z2 = 25.A) 8
B) 800
C)
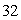
D) 400

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the surface integral 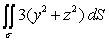 where is the portion of the cone
where is the portion of the cone 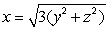 for 0 x 3.
for 0 x 3.
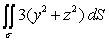 where is the portion of the cone
where is the portion of the cone 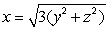 for 0 x 3.
for 0 x 3. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
68
Use Green's Theorem to evaluate 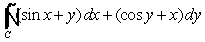 , where C is x2 + y2 = 16.
, where C is x2 + y2 = 16.
A) 6
B) 9
C) 18
D) 0
E) 12
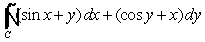 , where C is x2 + y2 = 16.
, where C is x2 + y2 = 16.A) 6
B) 9
C) 18
D) 0
E) 12

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
69
Use Green's Theorem to evaluate 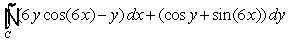 , where C is the circle
, where C is the circle 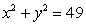 .
.
A)
B) 7
C) 49
D) 7
E) 0
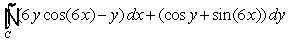 , where C is the circle
, where C is the circle 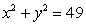 .
.A)
B) 7
C) 49
D) 7
E) 0

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the surface integral 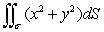 where is the portion of the cone
where is the portion of the cone 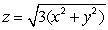 for 0 z 3.
for 0 z 3.
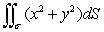 where is the portion of the cone
where is the portion of the cone 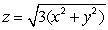 for 0 z 3.
for 0 z 3. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate the surface integral 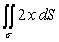 where is that portion of the plane x + 2y + 3z = 6 which lies in the first octant.
where is that portion of the plane x + 2y + 3z = 6 which lies in the first octant.
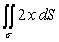 where is that portion of the plane x + 2y + 3z = 6 which lies in the first octant.
where is that portion of the plane x + 2y + 3z = 6 which lies in the first octant. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the surface integral 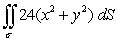 where is that portion of the cylinder x2 + z2 = 1 that lies above the xy-plane enclosed by 0 y 5.
where is that portion of the cylinder x2 + z2 = 1 that lies above the xy-plane enclosed by 0 y 5.
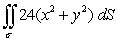 where is that portion of the cylinder x2 + z2 = 1 that lies above the xy-plane enclosed by 0 y 5.
where is that portion of the cylinder x2 + z2 = 1 that lies above the xy-plane enclosed by 0 y 5. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
73
Use Green's Theorem to evaluate 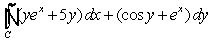 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.
A) 1/2
B) -5
C) 2
D) 0
E) 3
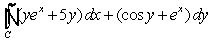 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.A) 1/2
B) -5
C) 2
D) 0
E) 3

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
74
Use Green's Theorem to evaluate 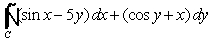 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.
A) 1/2
B) 2
C) 6
D) 0
E) 4
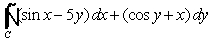 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.A) 1/2
B) 2
C) 6
D) 0
E) 4

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
75
Use Green's Theorem to evaluate 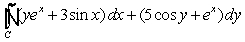 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.
A) 1/2
B) 1
C) 2
D) 0
E) 3
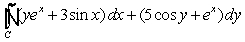 , where C is the square bounded by x = y = 0, and x = y = 1.
, where C is the square bounded by x = y = 0, and x = y = 1.A) 1/2
B) 1
C) 2
D) 0
E) 3

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the surface integral 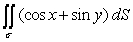 where is that portion of 3x + 3y + 3z = 3 which lies in the first octant.
where is that portion of 3x + 3y + 3z = 3 which lies in the first octant.
A)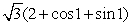
B) 0
C)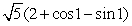
D)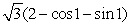
E)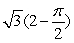
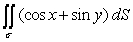 where is that portion of 3x + 3y + 3z = 3 which lies in the first octant.
where is that portion of 3x + 3y + 3z = 3 which lies in the first octant.A)
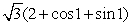
B) 0
C)
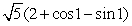
D)
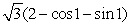
E)
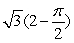

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate the surface integral 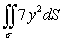 where is that portion of the plane x + y + z = 1 that lies in the first octant.
where is that portion of the plane x + y + z = 1 that lies in the first octant.
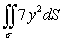 where is that portion of the plane x + y + z = 1 that lies in the first octant.
where is that portion of the plane x + y + z = 1 that lies in the first octant. 
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
78
Use Green's Theorem to evaluate 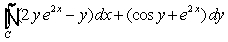 , where C is the circle
, where C is the circle 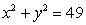 .
.
A) 0
B) 7
C) 49
D) 49
E)
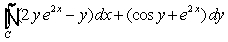 , where C is the circle
, where C is the circle 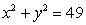 .
.A) 0
B) 7
C) 49
D) 49
E)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate the surface integral 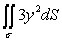 where is that portion of the cylinder y2 + z2 = 1 that lies above the xy-plane enclosed by 0 x 5 and -1 y 1.
where is that portion of the cylinder y2 + z2 = 1 that lies above the xy-plane enclosed by 0 x 5 and -1 y 1.
A)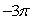
B)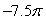
C)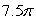
D)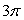
E) 0
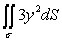 where is that portion of the cylinder y2 + z2 = 1 that lies above the xy-plane enclosed by 0 x 5 and -1 y 1.
where is that portion of the cylinder y2 + z2 = 1 that lies above the xy-plane enclosed by 0 x 5 and -1 y 1.A)
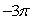
B)
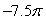
C)
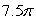
D)
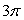
E) 0

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate the surface integral 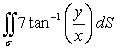 where is that portion of the paraboloid z = x2 + y2 enclosed by 1 z 9.
where is that portion of the paraboloid z = x2 + y2 enclosed by 1 z 9.
A)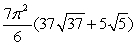
B)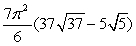
C) 0
D)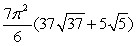
E)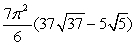
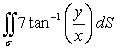 where is that portion of the paraboloid z = x2 + y2 enclosed by 1 z 9.
where is that portion of the paraboloid z = x2 + y2 enclosed by 1 z 9.A)
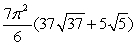
B)
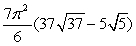
C) 0
D)
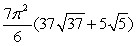
E)
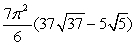

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck


