Deck 9: Confidence Intervals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/149
Play
Full screen (f)
Deck 9: Confidence Intervals
1
When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_bc1a_93a1_47dc084ca9f1_TB7056_11.jpg) (1 −
(1 − ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_e32b_93a1_93462c114577_TB7056_11.jpg) ) is larger than when
) is larger than when ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_e32c_93a1_958144d728f0_TB7056_11.jpg) (1 −
(1 − ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_e32d_93a1_f3f9f3bd03a2_TB7056_11.jpg) )] is smaller.
)] is smaller.
![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_bc1a_93a1_47dc084ca9f1_TB7056_11.jpg) (1 −
(1 − ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_e32b_93a1_93462c114577_TB7056_11.jpg) ) is larger than when
) is larger than when ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_e32c_93a1_958144d728f0_TB7056_11.jpg) (1 −
(1 − ![When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be narrower when (1 − ) is larger than when (1 − )] is smaller.](https://storage.examlex.com/TB7056/11ead627_0a82_e32d_93a1_f3f9f3bd03a2_TB7056_11.jpg) )] is smaller.
)] is smaller.False
2
The quantity 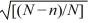 in the confidence intervals for μ and τ is called the finite population correction and is always less than 1.
in the confidence intervals for μ and τ is called the finite population correction and is always less than 1.
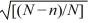 in the confidence intervals for μ and τ is called the finite population correction and is always less than 1.
in the confidence intervals for μ and τ is called the finite population correction and is always less than 1.True
3
The t distribution always has n degrees of freedom.
False
4
When solving for the sample size needed to compute a 95 percent confidence interval for a population proportion, p, having a given error bound, E, we choose a value of  that makes
that makes  (1 −
(1 −  ) as small as reasonably possible.
) as small as reasonably possible.
 that makes
that makes  (1 −
(1 −  ) as small as reasonably possible.
) as small as reasonably possible.
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
5
When the level of confidence and sample standard deviation remain the same, a confidence interval for a population mean based on a sample of n = 100 will be narrower than a confidence interval for a population mean based on a sample of n = 50.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
6
When determining the sample size (n) for a confidence interval for ρ, if you are using a previous sample, use the reasonable value of ρ that is closest to .25.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
7
If σ is unknown and there is no preliminary sample available to estimate σ, the range divided by four can be utilized to determine an estimate of σ when finding sample size.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
8
The standard error of the sample mean is σ/ 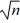 .
.
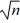 .
.
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
9
When determining the sample size, n, if the value found for n is 79.2, we would choose to sample 79 observations.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
10
The more variable that the population measurements are, the larger the sample size that is needed to accurately estimate µ at a specific confidence level.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
11
Assuming the same level of significance α, as the sample size increases, the value of tα/2 approaches the value of zα/2.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
12
When the level of confidence and sample proportion,  , remain the same, a confidence interval for a population proportion, p, based on a sample of n = 100 will be wider than a confidence interval for p based on a sample of n = 400.
, remain the same, a confidence interval for a population proportion, p, based on a sample of n = 100 will be wider than a confidence interval for p based on a sample of n = 400.
 , remain the same, a confidence interval for a population proportion, p, based on a sample of n = 100 will be wider than a confidence interval for p based on a sample of n = 400.
, remain the same, a confidence interval for a population proportion, p, based on a sample of n = 100 will be wider than a confidence interval for p based on a sample of n = 400.
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
13
When the margin of error is added to and subtracted from the sample mean, an interval is formed that will contain μ with a probability of (1 − α).

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
14
When constructing a confidence interval for a sample proportion, the t distribution is appropriate if the sample size is small.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
15
When determining the sample size (n) for a confidence interval for ρ, if past experience tells us that p is at least .8, use p = .2.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
16
When the level of confidence and the sample size remain the same, a confidence interval for a population mean, μ, will be wider when the sample standard deviation, s, is small than when s is large.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
17
When determining the sample size (n) for a confidence interval for ρ, if you have no idea what value p is (it could be any value between 0 and 1), use p = .5.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
18
When the population is normally distributed and the population standard deviation σ is unknown, then for any sample size n, the sampling distribution of  is based on the z distribution.
is based on the z distribution.
 is based on the z distribution.
is based on the z distribution.
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
19
First, a 90 percent confidence interval is constructed from a sample size of 100. Then, for the same identical data, a 92 percent confidence interval is constructed. The width of the 90 percent interval is wider than the 92 percent confidence interval.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
20
When the sample size and sample standard deviation remain the same, a 99 percent confidence interval for a population mean, μ, will be narrower than the 95 percent confidence interval for μ.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
21
A confidence interval increases in width as
A) the level of confidence increases.
B) n decreases.
C) s increases.
D) All of these answers are correct.
A) the level of confidence increases.
B) n decreases.
C) s increases.
D) All of these answers are correct.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
22
As standard deviation increases, sample size ________ to achieve a specified level of confidence.
A) increases
B) decreases
C) remains the same
A) increases
B) decreases
C) remains the same

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
23
When the population is normally distributed, population standard deviation σ is unknown, and the sample size is n = 15, the confidence interval for the population mean μ is based on
A) the z (normal) distribution.
B) the t distribution.
C) the binomial distribution.
D) the Poisson distribution.
E) None of these answers is correct.
A) the z (normal) distribution.
B) the t distribution.
C) the binomial distribution.
D) the Poisson distribution.
E) None of these answers is correct.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
24
When the level of confidence and sample proportion  remain the same, a confidence interval for a population proportion p based on a sample of n = 100 will be ________ a confidence interval for p based on a sample of n = 400.
remain the same, a confidence interval for a population proportion p based on a sample of n = 100 will be ________ a confidence interval for p based on a sample of n = 400.
A) wider than
B) narrower than
C) equal to
 remain the same, a confidence interval for a population proportion p based on a sample of n = 100 will be ________ a confidence interval for p based on a sample of n = 400.
remain the same, a confidence interval for a population proportion p based on a sample of n = 100 will be ________ a confidence interval for p based on a sample of n = 400.A) wider than
B) narrower than
C) equal to

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
25
A tolerance interval is always longer than a corresponding confidence interval.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
26
When the level of confidence and sample size remain the same, a confidence interval for a population proportion, p, will be ________ when  (1 −
(1 −  ) is larger than when
) is larger than when  (1 −
(1 −  ) is smaller.
) is smaller.
A) wider
B) narrower
C) neither wider nor narrower (they will be the same)
 (1 −
(1 −  ) is larger than when
) is larger than when  (1 −
(1 −  ) is smaller.
) is smaller.A) wider
B) narrower
C) neither wider nor narrower (they will be the same)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
27
When the sample size and the sample proportion  remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.
remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.
A) wider than
B) narrower than
C) equal to
 remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.
remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.A) wider than
B) narrower than
C) equal to

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
28
When determining the sample size, if the value found is not an integer initially, you should ________ choose the next highest integer value.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
29
When the sample size and sample standard deviation remain the same, a 99 percent confidence interval for a population mean, μ, will be ________ the 95 percent confidence interval for μ.
A) wider than
B) narrower than
C) equal to
A) wider than
B) narrower than
C) equal to

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
30
When constructing a confidence interval for a population mean, if a population is normally distributed and a small sample is taken, then the distribution of 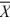 is based on ________.
is based on ________.
A) the z distribution
B) the t distribution
C) neither the z nor the t distribution
D) both the z and the t distribution
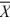 is based on ________.
is based on ________.A) the z distribution
B) the t distribution
C) neither the z nor the t distribution
D) both the z and the t distribution

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
31
The width of a confidence interval will be
A) narrower for 98 percent confidence than for 90 percent confidence.
B) wider for a sample size of 64 than for a sample size of 36.
C) wider for 99 percent confidence than for 95 percent confidence
D) narrower for a sample size of 25 than for a sample size of 36.
E) None of these answers is correct.
A) narrower for 98 percent confidence than for 90 percent confidence.
B) wider for a sample size of 64 than for a sample size of 36.
C) wider for 99 percent confidence than for 95 percent confidence
D) narrower for a sample size of 25 than for a sample size of 36.
E) None of these answers is correct.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
32
A tolerance interval is meant to contain a specified percentage of the individual population measurements.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
33
The exact spread of the t distribution depends on the ________.
A) standard deviation of the sample
B) sample size n
C) number of degrees of freedom
D) z distribution
A) standard deviation of the sample
B) sample size n
C) number of degrees of freedom
D) z distribution

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
34
Which of the following is an advantage of a confidence interval estimate over a point estimate for a population parameter?
A) Interval estimates are more precise than point estimates.
B) Interval estimates are less accurate than point estimates.
C) Interval estimates are both more accurate and more precise than point estimates.
D) Interval estimates take into account the fact that the statistic that is used to estimate the population parameter is a random variable.
A) Interval estimates are more precise than point estimates.
B) Interval estimates are less accurate than point estimates.
C) Interval estimates are both more accurate and more precise than point estimates.
D) Interval estimates take into account the fact that the statistic that is used to estimate the population parameter is a random variable.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
35
When the level of confidence and sample standard deviation remain the same, a confidence interval for a population mean based on a sample of n = 100 will be ________ a confidence interval for a population mean based on a sample of n = 50.
A) wider than
B) narrower than
C) equal to
A) wider than
B) narrower than
C) equal to

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
36
When the level of confidence and the sample size remain the same, a confidence interval for a population mean μ will be ________ when the sample standard deviation s is small than when s is large.
A) wider
B) narrower
C) neither wider nor narrower (they will be the same)
A) wider
B) narrower
C) neither wider nor narrower (they will be the same)

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
37
The width of a confidence interval will be
A) narrower for 99 percent confidence than for 95 percent confidence.
B) wider for a sample size of 100 than for a sample size of 50.
C) narrower for 90 percent confidence than for 95 percent confidence.
D) wider when the sample standard deviation (s) is small than when s is large.
A) narrower for 99 percent confidence than for 95 percent confidence.
B) wider for a sample size of 100 than for a sample size of 50.
C) narrower for 90 percent confidence than for 95 percent confidence.
D) wider when the sample standard deviation (s) is small than when s is large.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
38
The t distribution approaches the ________ distribution as the sample size ________.
A) binomial, increases
B) binomial, decreases
C) z, decreases
D) z, increases
A) binomial, increases
B) binomial, decreases
C) z, decreases
D) z, increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
39
A confidence interval for the population mean is meant to contain a specified percentage of the individual population measurements.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
40
When solving for the sample size needed to compute a 95 percent confidence interval for a population proportion p, having a given error bound E, we choose a value of  that
that
A) makes (1 −
(1 −
 ) as small as reasonably possible.
) as small as reasonably possible.
B) makes (1 −
(1 −
 ) as large as reasonably possible.
) as large as reasonably possible.
C) makes (1 −
(1 −
 ) as close to .5 as reasonably possible.
) as close to .5 as reasonably possible.
D) makes (1 −
(1 −
 ) as close to .25 as reasonably possible.
) as close to .25 as reasonably possible.
E) makes (1 −
(1 −
 ) as large as reasonably possible and makes
) as large as reasonably possible and makes
 (1 −
(1 −
 ) as close to .25 as reasonably possible.
) as close to .25 as reasonably possible.
 that
thatA) makes
 (1 −
(1 − ) as small as reasonably possible.
) as small as reasonably possible.B) makes
 (1 −
(1 − ) as large as reasonably possible.
) as large as reasonably possible.C) makes
 (1 −
(1 − ) as close to .5 as reasonably possible.
) as close to .5 as reasonably possible.D) makes
 (1 −
(1 − ) as close to .25 as reasonably possible.
) as close to .25 as reasonably possible.E) makes
 (1 −
(1 − ) as large as reasonably possible and makes
) as large as reasonably possible and makes (1 −
(1 − ) as close to .25 as reasonably possible.
) as close to .25 as reasonably possible.
Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
41
There is little difference between the values of tα/2 and zα/2 when
A) the sample size is small.
B) the sample size is large.
C) the sample mean is small.
D) the sample mean is large.
E) the sample standard deviation is small.
A) the sample size is small.
B) the sample size is large.
C) the sample mean is small.
D) the sample mean is large.
E) the sample standard deviation is small.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
42
In determining the sample size to estimate a population proportion, as p approaches .5, the calculated value of the sample size ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
43
If everything else is held constant, decreasing the margin of error causes the required sample size to ________.
A) stay the same
B) decrease
C) increase
A) stay the same
B) decrease
C) increase

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
44
The internal auditing staff of a local lawn-service company performs a sample audit each quarter to estimate the proportion of accounts that are delinquent (more than 90 days overdue). For this quarter, the auditing staff randomly selected 400 customer accounts and found that 80 of these accounts were delinquent. What is the 95 percent confidence interval for the proportion of all delinquent customer accounts at this company?
A) .1608 to .2392
B) .1992 to .2008
C) .1671 to .2329
D) .1485 to .2515
E) .1714 to .2286
A) .1608 to .2392
B) .1992 to .2008
C) .1671 to .2329
D) .1485 to .2515
E) .1714 to .2286

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
45
The tolerance interval of 95.44 percent is ________ a 95.44 percent confidence interval.
A) the same width as
B) narrower than
C) wider than
A) the same width as
B) narrower than
C) wider than

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
46
A confidence interval for the population mean is an interval constructed around the ________.
A) sample mean
B) population mean
C) z test statistic
D) t test statistic
A) sample mean
B) population mean
C) z test statistic
D) t test statistic

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
47
As the margin of error decreases, the width of the confidence interval ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
48
When constructing a confidence interval, as the confidence level required in estimating the mean increases, the width of the confidence interval ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
49
The internal auditing staff of a local lawn-service company performs a sample audit each quarter to estimate the proportion of accounts that are current (between 0 and 60 days after billing). The historical records show that over the past 8 years 70 percent of the accounts have been current. Determine the sample size needed in order to be 99 percent confident that the sample proportion of the current customer accounts is within .03 of the true proportion of all current accounts for this company.
A) 1842
B) 1549
C) 897
D) 632
E) 1267
A) 1842
B) 1549
C) 897
D) 632
E) 1267

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
50
In a manufacturing process a random sample of 9 manufactured bolts has a mean length of 3 inches with a standard deviation of .3 inches and is normally distributed. What is the 95 percent confidence interval for the true mean length of the manufactured bolt?
A) 2.804 to 3.196
B) 2.308 to 3.692
C) 2.769 to 3.231
D) 2.412 to 3.588
E) 2.814 to 3.186
A) 2.804 to 3.196
B) 2.308 to 3.692
C) 2.769 to 3.231
D) 2.412 to 3.588
E) 2.814 to 3.186

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
51
When a confidence interval for a population proportion is constructed for a sample size n = 30 and the value of  = .4, the interval is based on
= .4, the interval is based on
A) the z distribution.
B) the t distribution.
C) the exponential distribution.
D) the Poisson distribution.
E) None of these answers is correct.
 = .4, the interval is based on
= .4, the interval is based onA) the z distribution.
B) the t distribution.
C) the exponential distribution.
D) the Poisson distribution.
E) None of these answers is correct.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
52
As the sample size n increases, the width of the confidence interval ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
53
Assuming the same level of significance α, as the sample size increases, the value of tα/2 ________ approaches the value of zα/2.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
54
As the stated confidence level decreases, the width of the confidence interval ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
55
When establishing the confidence interval for the average weight of a cereal box, assume that the population standard deviation is known to be 2 ounces and is normally distributed. Based on a sample, the average weight of a sample of 20 boxes is 16 ounces. The appropriate test statistic to use is ________.
A) t
B) z
C) χ
D) p
A) t
B) z
C) χ
D) p

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
56
A researcher for a paint company is measuring the level of a certain chemical contained in a particular type of paint. If the paint contains too much of this chemical, the quality of the paint will be compromised. On average, each can of paint contains 10 percent of the chemical. How many cans of paint should the sample contain if the researcher wants to be 98 percent certain of being within 1 percent of the true proportion of this chemical?
A) 4870
B) 1107
C) 26
D) 645
A) 4870
B) 1107
C) 26
D) 645

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
57
As the significance level α increases, the width of the confidence interval ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
58
In a manufacturing process, a random sample of 36 manufactured bolts has a mean length of 3 inches with a standard deviation of .3 inches. What is the 99 percent confidence interval for the true mean length of the manufactured bolt?
A) 2.902 to 3.098
B) 2.884 to 3.117
C) 2.864 to 3.136
D) 2.228 to 3.772
E) 2.802 to 3.198
A) 2.902 to 3.098
B) 2.884 to 3.117
C) 2.864 to 3.136
D) 2.228 to 3.772
E) 2.802 to 3.198

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
59
As the standard deviation (σ) decreases, the width of the confidence interval ________.
A) stays the same
B) decreases
C) increases
A) stays the same
B) decreases
C) increases

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
60
In a manufacturing process, a random sample of 9 manufactured bolts has a mean length of 3 inches with a variance of .09 and is normally distributed. What is the 90 percent confidence interval for the true mean length of the manufactured bolt?
A) 2.8355 to 3.1645
B) 2.5065 to 3.4935
C) 2.4420 to 3.5580
D) 2.8140 to 3.1860
E) 2.9442 to 3.0558
A) 2.8355 to 3.1645
B) 2.5065 to 3.4935
C) 2.4420 to 3.5580
D) 2.8140 to 3.1860
E) 2.9442 to 3.0558

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
61
Health insurers and the federal government are both putting pressure on hospitals to shorten the average length of stay (LOS) of their patients. In 2003, the average LOS for non-heart patients was 4.6 days. A random sample of 20 hospitals in one state had a mean LOS for non-heart patients in 2008 of 3.8 days and a standard deviation of 1.2 days and is normally distributed. How large a sample of hospitals would we need to be 99 percent confident that the sample mean is within .5 days of the population mean?
A) 3
B) 7
C) 32
D) 48
E) 96
A) 3
B) 7
C) 32
D) 48
E) 96

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
62
The coffee and soup machine at the local subway station is supposed to fill cups with 6 ounces of soup. Ten cups of soup are bought with results of a mean of 5.93 ounces and a standard deviation of .13 ounces. How large a sample of soups would we need to be 95 percent confident that the sample mean is within .03 ounces of the population mean?
A) 97
B) 96
C) 73
D) 62
E) 10
A) 97
B) 96
C) 73
D) 62
E) 10

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
63
A company is interested in estimating μ, the mean number of days of sick leave taken by its employees. Their statistician randomly selects 100 personnel files and notes the number of sick days taken by each employee. The sample mean is 12.2 days, and the sample standard deviation is 10 days. Calculate a 95 percent confidence interval for μ.

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
64
In a study of factors affecting whether soldiers decide to reenlist, 320 subjects were measured for an index of satisfaction. The sample mean is 28.8 and the sample standard deviation is 7.3. Use the given sample data to construct the 98 percent confidence interval for the population mean for level of satisfaction.
A) [27.85, 29.75]
B) [27.96, 29.64]
C) [11.82, 45.78]
D) [28.75, 28.85]
E) [28.60, 29.00]
A) [27.85, 29.75]
B) [27.96, 29.64]
C) [11.82, 45.78]
D) [28.75, 28.85]
E) [28.60, 29.00]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
65
Unoccupied seats on flights cause airlines to lose revenue. Suppose a large airline wants to estimate its average number of unoccupied seats per flight over the past year. Two hundred and twenty-five flight records are randomly selected, and the number of unoccupied seats is noted, with a sample mean of 11.6 seats and a standard deviation of 4.1 seats. How many flights should we select if we wish to estimate μ to within 2 seats and be 95 percent confident?
A) 130
B) 65
C) 33
D) 17
E) 12
A) 130
B) 65
C) 33
D) 17
E) 12

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
66
In a manufacturing process, we are interested in measuring the average length of a certain type of bolt. Based on a preliminary sample of 9 manufactured bolts, the sample standard deviation is .3 inches. How many bolts should be sampled in order to make us 95 percent confident that the sample mean bolt length is within .02 inches of the true mean bolt length?

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
67
Researchers have studied the role that the age of workers has in determining the hours per month spent on personal tasks. A sample of 1,686 adults were observed for one month. The data follow. ![<strong>Researchers have studied the role that the age of workers has in determining the hours per month spent on personal tasks. A sample of 1,686 adults were observed for one month. The data follow. Construct a 98 percent confidence interval for the mean hours spent on personal tasks for 25- to 44-year-olds.</strong> A) [3.96, 4.12] B) [3.97, 4.11] C) [3.98, 4.10] D) [2.16, 5.92] E) [3.95, 4.13]](https://storage.examlex.com/TB7056/11ead627_0a85_c97d_93a1_a93a83af6439_TB7056_00.jpg) Construct a 98 percent confidence interval for the mean hours spent on personal tasks for 25- to 44-year-olds.
Construct a 98 percent confidence interval for the mean hours spent on personal tasks for 25- to 44-year-olds.
A) [3.96, 4.12]
B) [3.97, 4.11]
C) [3.98, 4.10]
D) [2.16, 5.92]
E) [3.95, 4.13]
![<strong>Researchers have studied the role that the age of workers has in determining the hours per month spent on personal tasks. A sample of 1,686 adults were observed for one month. The data follow. Construct a 98 percent confidence interval for the mean hours spent on personal tasks for 25- to 44-year-olds.</strong> A) [3.96, 4.12] B) [3.97, 4.11] C) [3.98, 4.10] D) [2.16, 5.92] E) [3.95, 4.13]](https://storage.examlex.com/TB7056/11ead627_0a85_c97d_93a1_a93a83af6439_TB7056_00.jpg) Construct a 98 percent confidence interval for the mean hours spent on personal tasks for 25- to 44-year-olds.
Construct a 98 percent confidence interval for the mean hours spent on personal tasks for 25- to 44-year-olds.A) [3.96, 4.12]
B) [3.97, 4.11]
C) [3.98, 4.10]
D) [2.16, 5.92]
E) [3.95, 4.13]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
68
The state highway department is studying traffic patterns on one of the busiest highways in the state. As part of the study, the department needs to estimate the average number of vehicles that pass an intersection each day. A random sample of 64 days gives us a sample mean of 14,205 cars and a sample standard deviation of 1,010 cars. After calculating the confidence interval, the highway department officials decide that the precision is too low for their needs. They feel the precision should be 300 cars. Given this precision, and needing to be 99 percent confident, how many days do they need to sample?
A) 109
B) 80
C) 79
D) 62
E) 9
A) 109
B) 80
C) 79
D) 62
E) 9

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
69
The coffee and soup machine at the local subway station is supposed to fill cups with 6 ounces of soup. Ten cups of soup are bought with results of a mean of 5.93 ounces and a standard deviation of .13 ounces. Construct a 99 percent confidence interval for the true machine-fill amount.
A) [5.75, 5.99]
B) [5.85, 6.05]
C) [5.90, 6.00]
D) [5.70, 6.16]
E) [5.80, 6.06]
A) [5.75, 5.99]
B) [5.85, 6.05]
C) [5.90, 6.00]
D) [5.70, 6.16]
E) [5.80, 6.06]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
70
In a manufacturing process, we are interested in measuring the average length of a certain type of bolt. Past data indicate that the standard deviation is .25 inches. How many manufactured bolts should be sampled in order to make us 95 percent confident that the sample mean bolt length is within .02 inches of the true mean bolt length?
A) 25
B) 49
C) 423
D) 601
E) 1225
A) 25
B) 49
C) 423
D) 601
E) 1225

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
71
A psychologist is collecting data on the time it takes to learn a certain task. For 50 randomly selected adult subjects, the sample mean is 16.40 minutes and the sample standard deviation is 4.00 minutes. Construct the 95 percent confidence interval for the mean time required by all adults to learn the task.
A) [8.56, 24.24]
B) [15.47, 17.33]
C) [16.24, 16.56]
D) [15.26, 17.54]
E) [17.12, 48.48]
A) [8.56, 24.24]
B) [15.47, 17.33]
C) [16.24, 16.56]
D) [15.26, 17.54]
E) [17.12, 48.48]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
72
In a random sample of 651 computer scientists who subscribed to a web-based daily news update, it was found that the average salary was $46,816 with a population standard deviation of $12,557. Calculate a 91 percent confidence interval for the mean salary of computer scientists.
A) [$25,469, $68,163]
B) [$46,592, $47,040]
C) [$46,157, $47,475]
D) [$46,783, $46,849]
E) [$45,981, $47,650]
A) [$25,469, $68,163]
B) [$46,592, $47,040]
C) [$46,157, $47,475]
D) [$46,783, $46,849]
E) [$45,981, $47,650]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
73
Unoccupied seats on flights cause airlines to lose revenue. Suppose a large airline wants to estimate its average number of unoccupied seats per flight over the past year. Two hundred and twenty-five flight records are randomly selected, and the number of unoccupied seats is noted, with a sample mean of 11.6 seats and a standard deviation of 4.1 seats. Calculate a 90 percent confidence interval for μ, the mean number of unoccupied seats per flight during the past year.
A) [4.86, 18.34]
B) [11.25, 11.95]
C) [11.57, 11.63]
D) [11.15, 12.05]
E) [11.30, 12.20]
A) [4.86, 18.34]
B) [11.25, 11.95]
C) [11.57, 11.63]
D) [11.15, 12.05]
E) [11.30, 12.20]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
74
The U.S. Department of Health and Human Services collected sample data for 772 males between the ages of 18 and 24. That sample group has a mean height of 69.7 inches with a standard deviation of 2.8 inches. Find the 99 percent confidence interval for the mean height of all males between the ages of 18 and 24.
A) [63.19, 76.21]
B) [62.49, 76.91]
C) [69.65, 69.75]
D) [69.47, 69.93]
E) [69.44, 69.96]
A) [63.19, 76.21]
B) [62.49, 76.91]
C) [69.65, 69.75]
D) [69.47, 69.93]
E) [69.44, 69.96]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
75
Health insurers and the federal government are both putting pressure on hospitals to shorten the average length of stay (LOS) of their patients. In 2003, the average LOS for non-heart patients was 4.6 days. A random sample of 20 hospitals in one state had a mean LOS for non-heart patients in 2008 of 3.8 days and a standard deviation of 1.2 days and is normally distributed. Calculate a 95 percent confidence interval for the population mean LOS for non-heart patients in these hospitals in 2008.
A) [3.24, 4.36]
B) [3.67, 3.93]
C) [3.34, 4.26]
D) [3.38, 4.22]
E) [3.27, 4.33]
A) [3.24, 4.36]
B) [3.67, 3.93]
C) [3.34, 4.26]
D) [3.38, 4.22]
E) [3.27, 4.33]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
76
A local company makes a candy that is supposed to weigh 1.00 ounces. A random sample of 25 pieces of candy produces a mean of .996 ounces with a standard deviation of .004 ounces. Construct a 98 percent confidence interval for the mean weight of all such candy.
A) [.9645, 1.0275]
B) [.9956, .9964]
C) [.9860, 1.0060]
D) [.9940, .9980]
E) [.9942, .9978]
A) [.9645, 1.0275]
B) [.9956, .9964]
C) [.9860, 1.0060]
D) [.9940, .9980]
E) [.9942, .9978]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
77
A company is interested in estimating μ, the mean number of days of sick leave taken by its employees. Their statistician randomly selects 100 personnel files and notes the number of sick days taken by each employee. The sample mean is 12.2 days, and the sample standard deviation is 10 days. How many personnel files would the statistician have to select in order to estimate μ to within 2 days with a 99 percent confidence interval?
A) 2
B) 13
C) 136
D) 165
E) 173
A) 2
B) 13
C) 136
D) 165
E) 173

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
78
A local company makes a candy that is supposed to weigh 1.00 ounces. A random sample of 25 pieces of candy produces a mean of .996 ounces with a standard deviation of .004 ounces. How many pieces of candy must we sample if we want to be 99 percent confident that the sample mean is within .001 ounces of the true mean?
A) 126
B) 124
C) 107
D) 12
E) 6
A) 126
B) 124
C) 107
D) 12
E) 6

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
79
At the end of 1990, 1991, and 1992, the average prices of a share of stock in a portfolio were $34.83, $34.65, and $31.26 respectively. To investigate the average share price at the end of 1993, a random sample of 30 stocks was drawn and their closing prices on the last trading day of 1993 were observed with a mean of 33.583 and a standard deviation of 19.149. Estimate the average price of a share of stock in the portfolio at the end of 1993 with a 90 percent confidence interval.
A) [27.643, 39.523]
B) [26.732, 40.434]
C) [32.514, 34.651]
D) [32.533, 34.633]
E) [32.269, 34.897]
A) [27.643, 39.523]
B) [26.732, 40.434]
C) [32.514, 34.651]
D) [32.533, 34.633]
E) [32.269, 34.897]

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck
80
The state highway department is studying traffic patterns on one of the busiest highways in the state. As part of the study, the department needs to estimate the average number of vehicles that pass an intersection each day. A random sample of 64 days gives us a sample mean of 14,205 cars and a sample standard deviation of 1,010 cars. What is the 98 percent confidence interval estimate of μ, the mean number of cars passing the intersection?

Unlock Deck
Unlock for access to all 149 flashcards in this deck.
Unlock Deck
k this deck


