Question 1

When a confidence interval for a population proportion is constructed for a sample size n = 30 and the value of   = .4, the interval is based on

Accepted Answer

A)  the z distribution. 
B)  the t distribution. 
C)  the exponential distribution. 
D)  the Poisson distribution. 
E)  None of these answers is correct. 
A)  the z distribution. 
B)  the t distribution. 
C)  the exponential distribution. 
D)  the Poisson distribution. 
E)  None of these answers is correct. A

Question 2

Unoccupied seats on flights cause airlines to lose revenue. Suppose a large airline wants to estimate its average number of unoccupied seats per flight over the past year. Two hundred and twenty-five flight records are randomly selected, and the number of unoccupied seats is noted, with a sample mean of 11.6 seats and a standard deviation of 4.1 seats. Calculate a 90 percent confidence interval for μ, the mean number of unoccupied seats per flight during the past year.

Accepted Answer

A)  [4.86, 18.34] 
B)  [11.25, 11.95] 
C)  [11.57, 11.63] 
D)  [11.15, 12.05] 
E)  [11.30, 12.20] 
A)  [4.86, 18.34] 
B)  [11.25, 11.95] 
C)  [11.57, 11.63] 
D)  [11.15, 12.05] 
E)  [11.30, 12.20] D

Question 3

When the level of confidence and sample standard deviation remain the same, a confidence interval for a population mean based on a sample of n = 100 will be ________ a confidence interval for a population mean based on a sample of n = 50.

Accepted Answer

A)  wider than 
B)  narrower than 
C)  equal to 
A)  wider than 
B)  narrower than 
C)  equal to B

Question 4

As the margin of error decreases, the width of the confidence interval ________.

Accepted Answer

A)  stays the same 
B)  decreases 
C)  increases 
A)  stays the same 
B)  decreases 
C)  increases

Question 5

A researcher for a paint company is measuring the level of a certain chemical contained in a particular type of paint. If the paint contains too much of this chemical, the quality of the paint will be compromised. On average, each can of paint contains 10 percent of the chemical. How many cans of paint should the sample contain if the researcher wants to be 98 percent certain of being within 1 percent of the true proportion of this chemical?

Accepted Answer

A)  4870 
B)  1107 
C)  26 
D)  645 
A)  4870 
B)  1107 
C)  26 
D)  645

Question 6

When the sample size and sample standard deviation remain the same, a 99 percent confidence interval for a population mean, μ, will be ________ the 95 percent confidence interval for μ.

Accepted Answer

A)  wider than 
B)  narrower than 
C)  equal to 
A)  wider than 
B)  narrower than 
C)  equal to

Question 7

The quality control manager of a tire company wishes to estimate the tensile strength of a standard size of rubber used to make a class of radial tires. A random sample of 61 pieces of rubber from different production batches is subjected to a stress test. The test measures the force (in pounds) needed to break the rubber. According to the sample results, the average pressure is 238.4 pounds with a population standard deviation of 35 pounds. Determine the 98 percent confidence interval.

Accepted Answer

A)  [227.96, 248.84] 
B)  [236.64, 240.16] 
C)  [233.63, 243.17] 
D)  [229.21, 247.59] 
A)  [227.96, 248.84] 
B)  [236.64, 240.16] 
C)  [233.63, 243.17] 
D)  [229.21, 247.59]

Question 8

What sample size is needed to estimate the proportion of highway speeders within 5 percent using a 90 percent confidence level?

Accepted Answer

A)  385 
B)  68 
C)  271 
D)  165 
A)  385 
B)  68 
C)  271 
D)  165

Question 9

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded 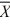  = 75 lb, and we know that σ2 = 100 lb. Calculate a 90 percent confidence interval for μ.

Accepted Answer

A)  [73.19, 76.81] 
B)  [51.74, 98.26] 
C)  [72.67, 77.33] 
D)  [67.50, 82.50] 
A)  [73.19, 76.81] 
B)  [51.74, 98.26] 
C)  [72.67, 77.33] 
D)  [67.50, 82.50]

Question 10

We want to estimate with 99 percent confidence the percentage of automobile purchasers who are under 30 years of age. A margin of error of 5 percentage points is desired. What sample size is needed? In an earlier sample, we found a 99 percent confidence interval of purchasers under 30 years of age to be [.18, .27] (use this figure for the sample proportion).

Accepted Answer

A)  104 
B)  664 
C)  392 
D)  463 
A)  104 
B)  664 
C)  392 
D)  463

Question 11

The 95 percent confidence interval for the average weight of a product is from 72.23 lb to 77.77 lb. Is μ = 77 a possible population mean using that 95 percent confidence interval?

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 12

When determining the sample size (n) for a confidence interval for ρ, if you are using a previous sample, use the reasonable value of ρ that is closest to .25.

Accepted Answer

A) True 
 B)False

Question 13

A psychologist is collecting data on the time it takes to learn a certain task. For 50 randomly selected adult subjects, the sample mean is 16.40 minutes and the sample standard deviation is 4.00 minutes. Construct the 95 percent confidence interval for the mean time required by all adults to learn the task.

Accepted Answer

A)  [8.56, 24.24] 
B)  [15.47, 17.33] 
C)  [16.24, 16.56] 
D)  [15.26, 17.54] 
E)  [17.12, 48.48] 
A)  [8.56, 24.24] 
B)  [15.47, 17.33] 
C)  [16.24, 16.56] 
D)  [15.26, 17.54] 
E)  [17.12, 48.48]

Question 14

When sample size is 16, find t.10.

Accepted Answer

1.341
df =

Question 15

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded 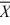  = 75 lb, and we know that σ2 = 100 lb. Calculate a 99 percent confidence interval for μ.

Accepted Answer

A)  [71.36, 78.64] 
B)  [74.25, 75.75] 
C)  [38.58, 111.42] 
D)  [71.71, 78.29] 
A)  [71.36, 78.64] 
B)  [74.25, 75.75] 
C)  [38.58, 111.42] 
D)  [71.71, 78.29]

Question 16

When the sample size and the sample proportion   remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.

Accepted Answer

A)  wider than 
B)  narrower than 
C)  equal to 
A)  wider than 
B)  narrower than 
C)  equal to

Question 17

The success rate of an experimental medical procedure is 37 per 120 cases in a sample. Find a 95 percent confidence interval for the actual success proportion of the procedure.

Accepted Answer

A)  [.2975, .4425] 
B)  [.2389, .3776] 
C)  [.2836, .4564] 
D)  [.2260, .3910] 
A)  [.2975, .4425] 
B)  [.2389, .3776] 
C)  [.2836, .4564] 
D)  [.2260, .3910]

Question 18

Unoccupied seats on flights cause airlines to lose revenue. Suppose a large airline wants to estimate its average number of unoccupied seats per flight over the past year. Two hundred and twenty-five flight records are randomly selected and the number of unoccupied seats is noted, with a sample mean of 11.6 seats and a standard deviation of 4.1 seats. Calculate a 95 percent confidence interval for μ, the mean number of unoccupied seats per flight during the past year.

Accepted Answer

A)  [11.06, 12.14] 
B)  [11.34, 11.86] 
C)  [10.44, 12.76] 
D)  [11.15, 12.05] 
E)  [3.56, 19.64] 
A)  [11.06, 12.14] 
B)  [11.34, 11.86] 
C)  [10.44, 12.76] 
D)  [11.15, 12.05] 
E)  [3.56, 19.64]

Question 19

When sample size is 20, find t.025.

Accepted Answer

2.093
df =

Question 20

A confidence interval for the population mean is meant to contain a specified percentage of the individual population measurements.

Accepted Answer

A) True 
 B)False

When a confidence interval for a population proportion is constructed for a sample size n = 30 and the value of = .4, the interval is based on

When the level of confidence and sample standard deviation remain the same, a confidence interval for a population mean based on a sample of n = 100 will be ________ a confidence interval for a population mean based on a sample of n = 50.

As the margin of error decreases, the width of the confidence interval ________.

When the sample size and sample standard deviation remain the same, a 99 percent confidence interval for a population mean, μ, will be ________ the 95 percent confidence interval for μ.

What sample size is needed to estimate the proportion of highway speeders within 5 percent using a 90 percent confidence level?

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded = 75 lb, and we know that σ² = 100 lb. Calculate a 90 percent confidence interval for μ.

The 95 percent confidence interval for the average weight of a product is from 72.23 lb to 77.77 lb. Is μ = 77 a possible population mean using that 95 percent confidence interval?

When determining the sample size (n) for a confidence interval for ρ, if you are using a previous sample, use the reasonable value of ρ that is closest to .25.

When sample size is 16, find t_.10.

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded = 75 lb, and we know that σ² = 100 lb. Calculate a 99 percent confidence interval for μ.

When the sample size and the sample proportion remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.

The success rate of an experimental medical procedure is 37 per 120 cases in a sample. Find a 95 percent confidence interval for the actual success proportion of the procedure.

When sample size is 20, find t_.025.

A confidence interval for the population mean is meant to contain a specified percentage of the individual population measurements.

An Introduction to Business Statistics and Analytics

Descriptive Statistics and Analytics: Tabular and Graphical Methods

Descriptive Statistics and Analytics: Numerical Methods

Probability and Probability Models

Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Hypothesis Testing

Statistical Inferences Based on Two Samples

Experimental Design and Analysis of Variance

Chi-Square Tests

Simple Linear Regression Analysis

Multiple Regression and Model Building

Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,

Time Series Forecasting and Index Numbers

Nonparametric Methods

Decision Theory

Filters

Exam 9: Confidence Intervals

When a confidence interval for a population proportion is constructed for a sample size n = 30 and the value of = .4, the interval is based on

When the level of confidence and sample standard deviation remain the same, a confidence interval for a population mean based on a sample of n = 100 will be ________ a confidence interval for a population mean based on a sample of n = 50.

As the margin of error decreases, the width of the confidence interval ________.

When the sample size and sample standard deviation remain the same, a 99 percent confidence interval for a population mean, μ, will be ________ the 95 percent confidence interval for μ.

What sample size is needed to estimate the proportion of highway speeders within 5 percent using a 90 percent confidence level?

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded = 75 lb, and we know that σ2 = 100 lb. Calculate a 90 percent confidence interval for μ.

The 95 percent confidence interval for the average weight of a product is from 72.23 lb to 77.77 lb. Is μ = 77 a possible population mean using that 95 percent confidence interval?

When determining the sample size (n) for a confidence interval for ρ, if you are using a previous sample, use the reasonable value of ρ that is closest to .25.

When sample size is 16, find t.10.

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded = 75 lb, and we know that σ2 = 100 lb. Calculate a 99 percent confidence interval for μ.

When the sample size and the sample proportion remain the same, a 90 percent confidence interval for a population proportion p will be ________ the 99 percent confidence interval for p.

The success rate of an experimental medical procedure is 37 per 120 cases in a sample. Find a 95 percent confidence interval for the actual success proportion of the procedure.

When sample size is 20, find t.025.

A confidence interval for the population mean is meant to contain a specified percentage of the individual population measurements.

An Introduction to Business Statistics and Analytics

Descriptive Statistics and Analytics: Tabular and Graphical Methods

Descriptive Statistics and Analytics: Numerical Methods

Probability and Probability Models

Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Hypothesis Testing

Statistical Inferences Based on Two Samples

Experimental Design and Analysis of Variance

Chi-Square Tests

Simple Linear Regression Analysis

Multiple Regression and Model Building

Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,

Time Series Forecasting and Index Numbers

Nonparametric Methods

Decision Theory

Filters

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded = 75 lb, and we know that σ² = 100 lb. Calculate a 90 percent confidence interval for μ.

When sample size is 16, find t_.10.

The weight of a product is measured in pounds. A sample of 50 units is taken from a recent production. The sample yielded = 75 lb, and we know that σ² = 100 lb. Calculate a 99 percent confidence interval for μ.

When sample size is 20, find t_.025.