Deck 13: Multiple Regression Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/90
Play
Full screen (f)
Deck 13: Multiple Regression Analysis
1
In a multiple regression analysis with N observations and k independent variables, the degrees of freedom for the residual error is given by (N - k - 1).
True
2
In a multiple regression model, the proportion of the variation of the dependent variable, y, accounted for the independent variables in the regression model is given by the coefficient of multiple correlation.
False
3
The F value that is used to test for the overall significance of a multiple regression model is calculated by dividing the sum of mean squares regression (SSreg)by the sum of squares error (SSerr).
False
4
If we reject H0: β1= β2=0 using the F-test, then we should conclude that both slopes are different from zero.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
5
The model y = 0 + 1x1 + 2x2 + is a second-order regression model.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
6
In the model y = 0 + 1x1 + 2x2 + 3x3 + ,y is the independent variable.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
7
The F value that is used to test for the overall significance of a multiple regression model is calculated by dividing the mean square regression (MSreg)by the mean square error (MSerr).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
8
The mean square error (MSerr)is calculated by dividing the sum of squares error (SSerr)by the number of degrees of freedom in the error (dferr).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
9
In a multiple regression analysis with N observations and k independent variables, the degrees of freedom for the residual error is given by (N - k).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
10
The model y = 0 + 1x1 + 2x2 + 3x3 + is a first-order regression model.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
11
Multiple t-tests are used to determine whether the independent variables in the regression model are significant.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
12
The standard error of the estimate of a multiple regression model is computed by taking the square root of the SSE divided by the degrees of freedom of error for the model.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
13
In the model y = 0 + 1x1 + 2x2 + 3x3 + , is a constant.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
14
The mean square error (MSerr)is calculated by dividing the sum of squares error (SSerr)by the number of observations in the data set (N).

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
15
Regression analysis with two dependent variables and two or more independent variables is called multiple regression.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
16
The standard error of the estimate of a multiple regression model is essentially the standard deviation of the residuals for the regression model.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
17
The F test is used to determine whether the overall regression model is significant.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
18
In the multiple regression model y = 0 + 1x1 + 2x2 + 3x3 + , the coefficients of the x variables are called partial regression coefficients.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
19
In a multiple regression model, the partial regression coefficient of an independent variable represents the increase in the y variable when that independent variable is increased by one unit if the values of all other independent variables are held constant.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
20
A slope in a multiple regression model is known as a partial slope because it ignores the effects of other explanatory variables.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
21
A multiple regression analysis produced the following tables. The sample size for this analysis is ____________.
A)19
B)17
C)34
D)15
E)18
A)19
B)17
C)34
D)15
E)18

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
22
A cost accountant is developing a regression model to predict the total cost of producing a batch of printed circuit boards as a linear function of batch size (the number of boards produced in one lot or batch), production plant (Kingsland, and Yorktown), and production shift (day, and evening).In this model, "shift" is ______.
A)a response variable
B)an independent variable
C)a quantitative variable
D)a dependent variable
E)a constant
A)a response variable
B)an independent variable
C)a quantitative variable
D)a dependent variable
E)a constant

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
23
A cost accountant is developing a regression model to predict the total cost of producing a batch of printed circuit boards as a linear function of batch size (the number of boards produced in one lot or batch), production plant (Kingsland, and Yorktown), and production shift (day, and evening).The response variable in this model is ______.
A)batch size
B)production shift
C)production plant
D)total cost
E)variable cost
A)batch size
B)production shift
C)production plant
D)total cost
E)variable cost

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
24
The multiple regression formulas used to estimate the regression coefficients are designed to ________________.
A)minimize the total sum of squares (SST)
B)minimize the sum of squares of error (SSE)
C)maximize the standard error of the estimate
D)maximize the p-value for the calculated F value
E)minimize the mean error
A)minimize the total sum of squares (SST)
B)minimize the sum of squares of error (SSE)
C)maximize the standard error of the estimate
D)maximize the p-value for the calculated F value
E)minimize the mean error

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
25
A market analyst is developing a regression model to predict monthly household expenditures on groceries as a function of family size, household income, and household neighborhood (urban, suburban, and rural).The response variable in this model is _____.
A)family size
B)expenditures on groceries
C)household income
D)suburban
E)household neighborhood
A)family size
B)expenditures on groceries
C)household income
D)suburban
E)household neighborhood

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
26
Minitab and Excel output for a multiple regression model show the t tests for the regression coefficients but do not provide a t test for the regression constant.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
27
A multiple regression analysis produced the following tables. 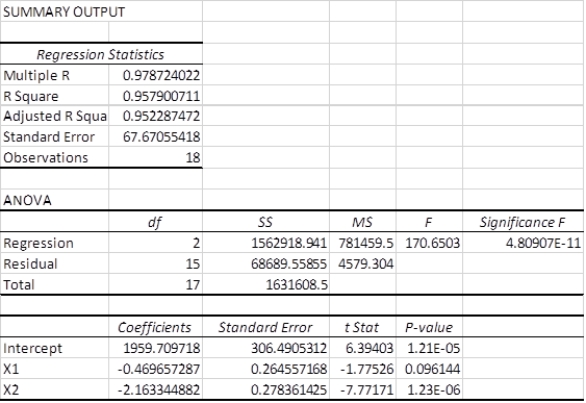 The regression equation for this analysis is ____________.
The regression equation for this analysis is ____________.
A)ŷ = 1959.71 + 0.46 x1 + 2.16 x2
B)ŷ = 1959.71 - 0.46 x1 + 2.16 x2
C)ŷ = 1959.71 - 0.46 x1 - 2.16 x2
D)ŷ =1959.71 + 0.46 x1 - 2.16 x2
E)ŷ =- 0.46 x1 - 2.16 x2
 The regression equation for this analysis is ____________.
The regression equation for this analysis is ____________.A)ŷ = 1959.71 + 0.46 x1 + 2.16 x2
B)ŷ = 1959.71 - 0.46 x1 + 2.16 x2
C)ŷ = 1959.71 - 0.46 x1 - 2.16 x2
D)ŷ =1959.71 + 0.46 x1 - 2.16 x2
E)ŷ =- 0.46 x1 - 2.16 x2

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
28
The value of adjusted R2 always goes up when a nontrivial explanatory variable is added to a regression model.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
29
A market analyst is developing a regression model to predict monthly household expenditures on groceries as a function of family size, household income, and household neighborhood (urban, suburban, and rural).The "income" variable in this model is ____.
A)an indicator variable
B)a response variable
C)a qualitative variable
D)a dependent variable
E)an independent variable
A)an indicator variable
B)a response variable
C)a qualitative variable
D)a dependent variable
E)an independent variable

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
30
A multiple regression analysis produced the following tables. 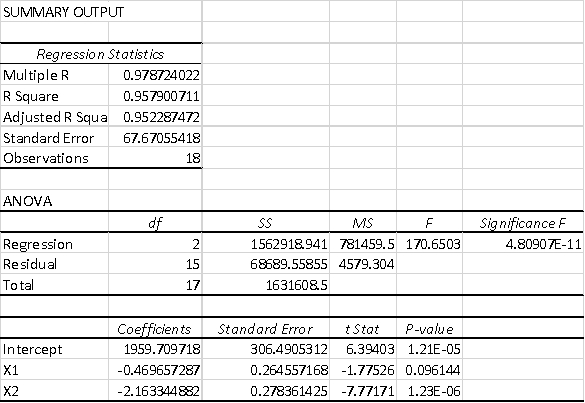 For x1= 360 and x2 = 220, the predicted value of y is ____________.
For x1= 360 and x2 = 220, the predicted value of y is ____________.
A)1314.70
B)1959.71
C)1077.58
D)2635.19
E)2265.57
 For x1= 360 and x2 = 220, the predicted value of y is ____________.
For x1= 360 and x2 = 220, the predicted value of y is ____________.A)1314.70
B)1959.71
C)1077.58
D)2635.19
E)2265.57

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
31
Minitab and Excel output for a multiple regression model show the F test for the overall model, but do not provide the t tests for the regression coefficients.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
32
A human resources analyst is developing a regression model to predict electricity plant manager compensation as a function of production capacity of the plant, number of employees at the plant, and plant technology (coal, oil, and nuclear).The response variable in this model is ______.
A)plant manager compensation
B)plant capacity
C)number of employees
D)plant technology
E)nuclear
A)plant manager compensation
B)plant capacity
C)number of employees
D)plant technology
E)nuclear

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
33
A real estate appraiser is developing a regression model to predict the market value of single-family residential houses as a function of heated area, number of bedrooms, number of bathrooms, age of the house, and central heating (yes, no).The "central heating" variable in this model is _______.
A)a response variable
B)an independent variable
C)a quantitative variable
D)a dependent variable
E)a constant
A)a response variable
B)an independent variable
C)a quantitative variable
D)a dependent variable
E)a constant

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
34
A human resources analyst is developing a regression model to predict electricity plant manager compensation as a function of production capacity of the plant, number of employees at the plant, and plant technology (coal, oil, and nuclear).The "number of employees at the plant" variable in this model is ______.
A)a qualitative variable
B)a dependent variable
C)a response variable
D)an indicator variable
E)an independent variable
A)a qualitative variable
B)a dependent variable
C)a response variable
D)an indicator variable
E)an independent variable

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
35
A multiple regression analysis produced the following tables. The regression equation for this analysis is ____________.
A)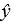 = 616.6849 + 3.33833 x1 + 1.780075 x2
= 616.6849 + 3.33833 x1 + 1.780075 x2
B)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 154.5535 - 1.43058 x1 + 5.30407 x2
C)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 616.6849 - 3.33833 x1 - 1.780075 x2
D)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 154.5535 + 2.333548 x1 + 0.335605 x2
E)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 616.6849 - 3.33833 x1 + 1.780075 x2
A)
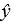 = 616.6849 + 3.33833 x1 + 1.780075 x2
= 616.6849 + 3.33833 x1 + 1.780075 x2B)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 154.5535 - 1.43058 x1 + 5.30407 x2
C)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 616.6849 - 3.33833 x1 - 1.780075 x2
D)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 154.5535 + 2.333548 x1 + 0.335605 x2
E)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 616.6849 - 3.33833 x1 + 1.780075 x2

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
36
The value of R2 always goes up when a nontrivial explanatory variable is added to a regression model.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
37
A human resources analyst is developing a regression model to predict electricity plant manager compensation as a function of production capacity of the plant, number of employees at the plant, and plant technology (coal, oil, and nuclear).The "plant technology" variable in this model is ______.
A)a response variable
B)a dependent variable
C)a quantitative variable
D)an independent variable
E)a constant
A)a response variable
B)a dependent variable
C)a quantitative variable
D)an independent variable
E)a constant

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
38
A market analyst is developing a regression model to predict monthly household expenditures on groceries as a function of family size, household income, and household neighborhood (urban, suburban, and rural).The "neighborhood" variable in this model is ______.
A)an independent variable
B)a response variable
C)a quantitative variable
D)a dependent variable
E)a constant
A)an independent variable
B)a response variable
C)a quantitative variable
D)a dependent variable
E)a constant

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
39
A cost accountant is developing a regression model to predict the total cost of producing a batch of printed circuit boards as a linear function of batch size (the number of boards produced in one lot or batch), production plant (Kingsland, and Yorktown), and production shift (day, and evening).In this model, "batch size" is ______.
A)a response variable
B)an indicator variable
C)a dependent variable
D)a qualitative variable
E)an independent variable
A)a response variable
B)an indicator variable
C)a dependent variable
D)a qualitative variable
E)an independent variable

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
40
A real estate appraiser is developing a regression model to predict the market value of single-family residential houses as a function of heated area, number of bedrooms, number of bathrooms, age of the house, and central heating (yes, no).The response variable in this model is _______.
A)heated area
B)number of bedrooms
C)market value
D)central heating
E)residential houses
A)heated area
B)number of bedrooms
C)market value
D)central heating
E)residential houses

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
41
A multiple regression analysis produced the following tables. These results indicate that ____________.
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is the only predictor variable significant at the 5% level
D)x2 is the only predictor variable significant at the 5% level
E)the intercept is not significant at the 5% level
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is the only predictor variable significant at the 5% level
D)x2 is the only predictor variable significant at the 5% level
E)the intercept is not significant at the 5% level

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
42
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The value of the standard error of the estimate se is __________.
A)13.23
B)3.16
C)17.32
D)26.46
E)10.00
A)13.23
B)3.16
C)17.32
D)26.46
E)10.00

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
43
A multiple regression analysis produced the following tables. These results indicate that ____________.
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is significant at the 5% level
D)x2 is significant at the 5% level
E)the intercept is not significant at 5% level
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is significant at the 5% level
D)x2 is significant at the 5% level
E)the intercept is not significant at 5% level

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
44
A multiple regression analysis produced the following tables. 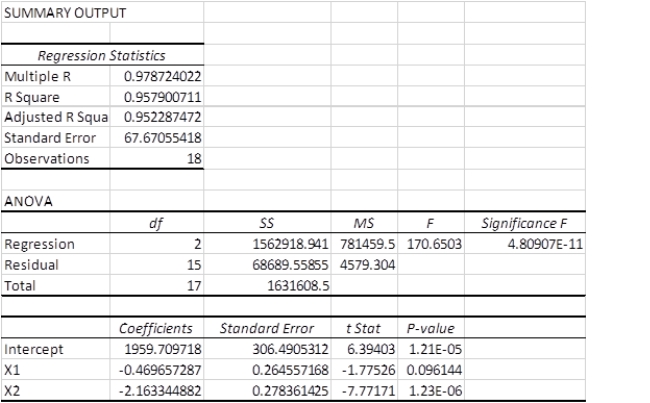 Using = 0.05 to test the null hypothesis H0: 1 = 0, the correct decision is ____.
Using = 0.05 to test the null hypothesis H0: 1 = 0, the correct decision is ____.
A)fail to reject the null hypothesis
B)reject the null hypothesis
C)fail to reject the alternative hypothesis
D)reject the alternative hypothesis
E)there is not enought information provided to make a decision
 Using = 0.05 to test the null hypothesis H0: 1 = 0, the correct decision is ____.
Using = 0.05 to test the null hypothesis H0: 1 = 0, the correct decision is ____.A)fail to reject the null hypothesis
B)reject the null hypothesis
C)fail to reject the alternative hypothesis
D)reject the alternative hypothesis
E)there is not enought information provided to make a decision

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
45
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The number of degrees of freedom for this regression is __________.
A)1
B)4
C)34
D)30
E)35
A)1
B)4
C)34
D)30
E)35

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
46
A multiple regression analysis produced the following tables. Using = 0.01 to test the null hypothesis H0: 1 = 2 = 0, the critical F value is ____.
A)8.68
B)6.36
C)8.40
D)6.11
E)3.36
A)8.68
B)6.36
C)8.40
D)6.11
E)3.36

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
47
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The MSE value is __________.
A)8.57
B)8.82
C)10.00
D)75.00
E)20.00
A)8.57
B)8.82
C)10.00
D)75.00
E)20.00

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
48
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The adjusted R2 value is __________.
A)0.80
B)0.70
C)0.66
D)0.76
E)0.30
A)0.80
B)0.70
C)0.66
D)0.76
E)0.30

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
49
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The MSR value is __________.
A)700.00
B)350.00
C)233.33
D)175.00
E)275.00
A)700.00
B)350.00
C)233.33
D)175.00
E)275.00

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
50
A multiple regression analysis produced the following tables. 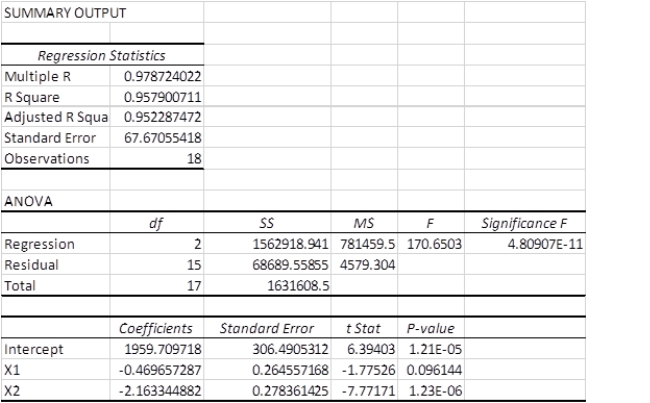 These results indicate that ____________.
These results indicate that ____________.
A)none of the predictor variables are significant at the 10% level
B)each predictor variable is significant at the 10% level
C)x1 is significant at the 10% level
D)x2 is significant at the 10% level
E)the intercept is not significant at 10% level
 These results indicate that ____________.
These results indicate that ____________.A)none of the predictor variables are significant at the 10% level
B)each predictor variable is significant at the 10% level
C)x1 is significant at the 10% level
D)x2 is significant at the 10% level
E)the intercept is not significant at 10% level

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
51
A multiple regression analysis produced the following tables. 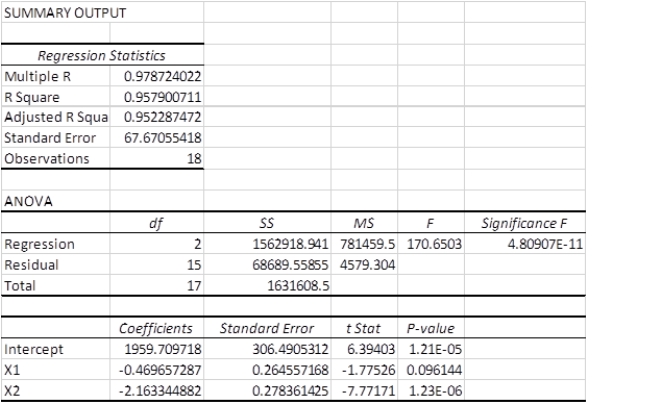 Using = 0.05 to test the null hypothesis H0: 2 = 0, the correct decision is ____.
Using = 0.05 to test the null hypothesis H0: 2 = 0, the correct decision is ____.
A)fail to reject the null hypothesis
B)reject the null hypothesis
C)fail to reject the alternative hypothesis
D)reject the alternative hypothesis
E)there is not enought information provided to make a decision
 Using = 0.05 to test the null hypothesis H0: 2 = 0, the correct decision is ____.
Using = 0.05 to test the null hypothesis H0: 2 = 0, the correct decision is ____.A)fail to reject the null hypothesis
B)reject the null hypothesis
C)fail to reject the alternative hypothesis
D)reject the alternative hypothesis
E)there is not enought information provided to make a decision

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
52
A multiple regression analysis produced the following tables. 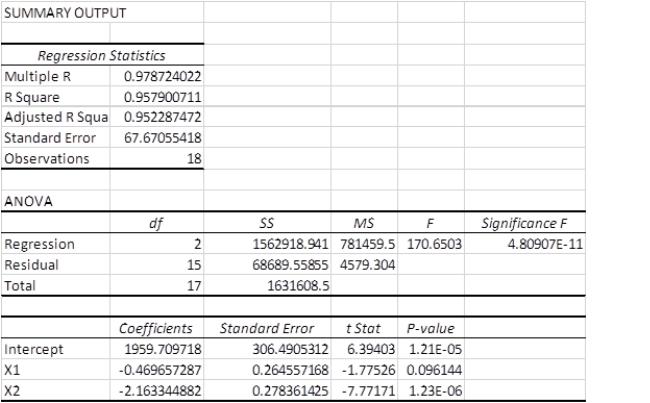 Using = 0.01 to test the model, these results indicate that ____________.
Using = 0.01 to test the model, these results indicate that ____________.
A)at least one of the regression variables is a significant predictor of y
B)none of the regression variables are significant predictors of y
C)y cannot be sufficiently predicted using these data
D)y is a good predictor of the regression variables in the model
E)the y intercept in this model is the best predictor variable
 Using = 0.01 to test the model, these results indicate that ____________.
Using = 0.01 to test the model, these results indicate that ____________.A)at least one of the regression variables is a significant predictor of y
B)none of the regression variables are significant predictors of y
C)y cannot be sufficiently predicted using these data
D)y is a good predictor of the regression variables in the model
E)the y intercept in this model is the best predictor variable

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
53
A multiple regression analysis produced the following tables. Using = 0.10 to test the null hypothesis H0: 2 = 0, the critical t value is ____.
A)±1.345
B)±1.356
C)±1.761
D)±2.782
E)±1.782
A)±1.345
B)±1.356
C)±1.761
D)±2.782
E)±1.782

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
54
In regression analysis, outliers may be identified by examining the ________.
A)coefficient of determination
B)coefficient of correlation
C)p-values for the partial coefficients
D)residuals
E)R-squared value
A)coefficient of determination
B)coefficient of correlation
C)p-values for the partial coefficients
D)residuals
E)R-squared value

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
55
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The R2 value is __________.
A)0.80
B)0.70
C)0.66
D)0.76
E)0.30
A)0.80
B)0.70
C)0.66
D)0.76
E)0.30

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
56
A multiple regression analysis produced the following tables. Using = 0.05 to test the null hypothesis H0: 1 = 0, the critical t value is ____.
A)± 1.753
B)± 2.110
C)± 2.131
D)± 1.740
E)± 2.500
A)± 1.753
B)± 2.110
C)± 2.131
D)± 1.740
E)± 2.500

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
57
A multiple regression analysis produced the following tables. Using = 0.05 to test the null hypothesis H0: 1 = 2 = 0, the critical F value is ____.
A)3.74
B)3.89
C)4.75
D)4.60
E)2.74
A)3.74
B)3.89
C)4.75
D)4.60
E)2.74

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
58
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The observed F value is __________.
A)17.50
B)2.33
C)0.70
D)0.43
E)0.50
A)17.50
B)2.33
C)0.70
D)0.43
E)0.50

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
59
A multiple regression analysis produced the following tables. 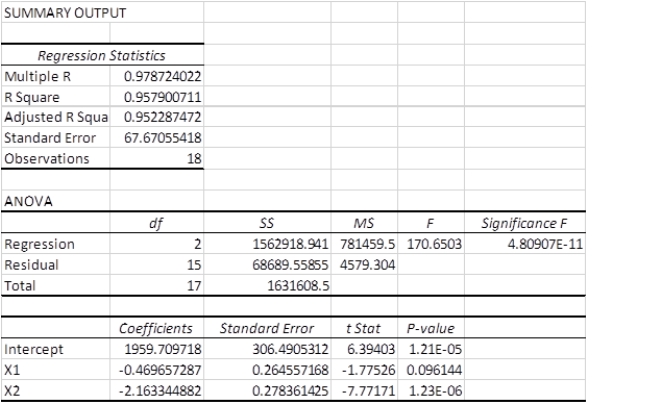 The sample size for this analysis is ____________.
The sample size for this analysis is ____________.
A)12
B)15
C)17
D)18
E)24
 The sample size for this analysis is ____________.
The sample size for this analysis is ____________.A)12
B)15
C)17
D)18
E)24

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
60
The following ANOVA table is from a multiple regression analysis with n = 35 and four independent variables. The number of degrees of freedom for error is __________.
A)1
B)4
C)34
D)30
E)35
A)1
B)4
C)34
D)30
E)35

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
61
A multiple regression analysis produced the following tables. The regression equation for this analysis is ____________.
A)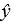 = 302689 + 1153309 x1 + 1455998 x2
= 302689 + 1153309 x1 + 1455998 x2
B)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = -139.609 + 24.24619 x1 + 32.10171 x2
C)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 2548.989 + 22.25267 x1 + 17.44559 x2
D)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = -0.05477 + 1.089586 x1 + 1.840105 x2
E)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 0.05477 + 1.089586 x1 + 1.840105 x2
A)
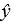 = 302689 + 1153309 x1 + 1455998 x2
= 302689 + 1153309 x1 + 1455998 x2B)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = -139.609 + 24.24619 x1 + 32.10171 x2
C)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 2548.989 + 22.25267 x1 + 17.44559 x2
D)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = -0.05477 + 1.089586 x1 + 1.840105 x2
E)11efcd22_071b_cfd6_b057_0f6ae9b62e31_TB7041_00 = 0.05477 + 1.089586 x1 + 1.840105 x2

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
62
A multiple regression analysis produced the following tables. The sample size for this analysis is ____________.
A)17
B)13
C)16
D)11
E)15
A)17
B)13
C)16
D)11
E)15

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
63
The following ANOVA table is from a multiple regression analysis. The MSE value is closest to__________.
A)31
B)500
C)16
D)2300
E)8.7
A)31
B)500
C)16
D)2300
E)8.7

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
64
The following ANOVA table is from a multiple regression analysis. The observed F value is __________.
A)16.25
B)30.77
C)500
D)0.049
E)0.039
A)16.25
B)30.77
C)500
D)0.049
E)0.039

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
65
A multiple regression analysis produced the following tables. For x1= 40 and x2 = 90, the predicted value of y is ____________.
A)753.77
B)1,173.00
C)1,355.26
D)3,719.39
E)1,565.75
A)753.77
B)1,173.00
C)1,355.26
D)3,719.39
E)1,565.75

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
66
The following ANOVA table is from a multiple regression analysis. The R2 value is __________.
A)0.65
B)0.53
C)0.35
D)0.43
E)1.37
A)0.65
B)0.53
C)0.35
D)0.43
E)1.37

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
67
A multiple regression analysis produced the following tables. These results indicate that ____________.
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is the only predictor variable significant at the 5% level
D)x2 is the only predictor variable significant at the 5% level
E)the intercept is not significant at 5% level
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is the only predictor variable significant at the 5% level
D)x2 is the only predictor variable significant at the 5% level
E)the intercept is not significant at 5% level

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
68
The following ANOVA table is from a multiple regression analysis. The sample size for the analysis is __________.
A)30
B)26
C)3
D)29
E)31
A)30
B)26
C)3
D)29
E)31

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
69
A multiple regression analysis produced the following tables. Using = 0.01 to test the null hypothesis H0: 2 = 0, the critical t value is ____.
A)± 1.174
B)± 2.093
C)± 2.131
D)± 4.012
E)± 3.012
A)± 1.174
B)± 2.093
C)± 2.131
D)± 4.012
E)± 3.012

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
70
The following ANOVA table is from a multiple regression analysis. The value of the standard error of the estimate se is __________.
A)30.77
B)5.55
C)4.03
D)3.20
E)0.73
A)30.77
B)5.55
C)4.03
D)3.20
E)0.73

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
71
A multiple regression analysis produced the following tables. The coefficient of multiple determination is ____________.
A)0.0592
B)0.9138
C)0.1149
D)0.9559
E)1.0000
A)0.0592
B)0.9138
C)0.1149
D)0.9559
E)1.0000

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
72
The following ANOVA table is from a multiple regression analysis. The MSR value is __________.
A)1500
B)50
C)2300
D)500
E)31
A)1500
B)50
C)2300
D)500
E)31

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
73
The following ANOVA table is from a multiple regression analysis. The adjusted R2 value is __________.
A)0.65
B)0.39
C)0.61
D)0.53
E)0.78
A)0.65
B)0.39
C)0.61
D)0.53
E)0.78

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
74
The following ANOVA table is from a multiple regression analysis. The number of independent variables in the analysis is __________.
A)30
B)26
C)1
D)3
E)2
A)30
B)26
C)1
D)3
E)2

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
75
A multiple regression analysis produced the following tables. Using = 0.01 to test the null hypothesis H0: 1 = 2 = 0, the critical F value is ____.
A)5.99
B)5.70
C)1.96
D)4.84
E)6.70
A)5.99
B)5.70
C)1.96
D)4.84
E)6.70

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
76
A multiple regression analysis produced the following tables. The coefficient of multiple determination is ____________.
A)0.2079
B)0.0860
C)0.5440
D)0.7921
E)0.5000
A)0.2079
B)0.0860
C)0.5440
D)0.7921
E)0.5000

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
77
A multiple regression analysis produced the following tables. The adjusted R2 is ____________.
A)0.9138
B)0.9408
C)0.8981
D)0.8851
E)0.8891
A)0.9138
B)0.9408
C)0.8981
D)0.8851
E)0.8891

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
78
A multiple regression analysis produced the following tables. For x1= 30 and x2 = 100, the predicted value of y is ____________.
A)753.77
B)1,173.00
C)1,355.26
D)615.13
E)6153.13
A)753.77
B)1,173.00
C)1,355.26
D)615.13
E)6153.13

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
79
A multiple regression analysis produced the following tables. These results indicate that ____________.
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is the only predictor variable significant at the 5% level
D)x2 is the only predictor variable significant at the 5% level
E)all variables are significant at 5% level
A)none of the predictor variables are significant at the 5% level
B)each predictor variable is significant at the 5% level
C)x1 is the only predictor variable significant at the 5% level
D)x2 is the only predictor variable significant at the 5% level
E)all variables are significant at 5% level

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
80
The following ANOVA table is from a multiple regression analysis. The SSE value is __________.
A)30
B)1500
C)500
D)800
E)2300
A)30
B)1500
C)500
D)800
E)2300

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck


