Deck 15: Chi-Squared Tests
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/175
Play
Full screen (f)
Deck 15: Chi-Squared Tests
1
In conducting a chi-squared goodness-of-fit test, an essential condition is that all expected frequencies are at least five.
True
2
The only way the chi-squared test statistic can be zero is if the observed frequencies are all exactly the same as the expected frequencies.
True
3
The total of the observed frequencies in a multinomial experiment must equal nk where n is the number of trials and k is the number of categories.
False
4
A multinomial experiment with two categories is identical to a binomial experiment.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
5
If the observed frequencies are all smaller than the expected frequencies in a goodness-of-fit test, the chi-squared test statistic will be negative.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
6
A left-tailed area in the chi-squared distribution equals .10.For 5 degrees of freedom the table value equals 9.23635.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
7
All of the expected frequencies in a chi-squared goodness-of-fit test must be equal to each other.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
8
A chi-squared goodness-of-fit test is always a two-tailed test.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
9
A chi-squared test is used to describe a population of nominal data.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
10
The alternative hypothesis in a goodness-of-fit test is that none of the pi values are equal to their values specified in H0.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
11
A left-tailed area in the chi-squared distribution equals .90.For 10 degrees of freedom the table value equals 15.9871.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
12
You cannot use a chi-squared goodness-of-fit test when there are only two possible outcomes for each trial in your experiment.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
13
In a goodness-of-fit test, all of the proportions specified in the null hypothesis must be equal to each other.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
14
For a chi-squared distributed random variable with 12 degrees of freedom and a level of significance of .05, the test statistics is 25.168.The chi-squared value from the table is 21.0261.These results will lead us to reject the null hypothesis.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
15
If there are only two categories, the chi-squared goodness-of-fit test is the same as the z-test for p, the population proportion (as long as the sample/cell sizes meet the conditions).

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
16
If the expected frequency of a cell is less than 5, you should combine cells of the table.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
17
A chi-squared distribution is symmetric.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
18
If the expected frequency of a cell is less than 5, you should increase the significance level.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
19
A small chi-squared test statistic in a goodness-of-fit test supports the null hypothesis.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
20
For a chi-squared distributed random variable with 10 degrees of freedom and a level of significance of .025, the chi-squared table value is 20.4831.Suppose the value of your test statistic is 16.857.This will lead you to reject the null hypothesis.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
21
How does a multinomial distribution differ from a binomial distribution?
A) A binomial has only two possible categories and a multinomial can have more.
B) A binomial has a fixed number of n trials.A multinomial has a fixed number of nk trials, where k is the number of categories.
C) The probabilities in a binomial distribution are always p and 1 - p.The trials in a multinomial distribution are always p/k and (1 - p/k).
D) All of these choices are true.
A) A binomial has only two possible categories and a multinomial can have more.
B) A binomial has a fixed number of n trials.A multinomial has a fixed number of nk trials, where k is the number of categories.
C) The probabilities in a binomial distribution are always p and 1 - p.The trials in a multinomial distribution are always p/k and (1 - p/k).
D) All of these choices are true.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
22
The sampling distribution of the test statistic for a goodness-of-fit test with k categories is a:
A) chi-squared distribution with k -1 degrees of freedom.
B) normal distribution.
C) Student t-distribution with k - 1 degrees of freedom.
D) None of these choices.
A) chi-squared distribution with k -1 degrees of freedom.
B) normal distribution.
C) Student t-distribution with k - 1 degrees of freedom.
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following conditions indicate that H0 should be rejected in a goodness-of-fit test?
A) The observed frequencies are equal to their expected frequencies.
B) The test statistic is large.
C) The degrees of freedom is large.
D) All of these choices are true.
A) The observed frequencies are equal to their expected frequencies.
B) The test statistic is large.
C) The degrees of freedom is large.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
24
Of the values for a chi-squared test statistic listed below, which one is most likely to lead to rejecting the null hypothesis in a goodness-of-fit test?
A) 0
B) .05
C) 1.96
D) 45
A) 0
B) .05
C) 1.96
D) 45

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
25
If we use the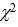 goodness-of-fit to test for the differences among 4 proportions, the degrees of freedom is equal to:
goodness-of-fit to test for the differences among 4 proportions, the degrees of freedom is equal to:
A) 3
B) 4
C) 5
D) None of these choices.
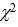 goodness-of-fit to test for the differences among 4 proportions, the degrees of freedom is equal to:
goodness-of-fit to test for the differences among 4 proportions, the degrees of freedom is equal to:A) 3
B) 4
C) 5
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
26
Which of the following represents H1 in a chi-squared goodness-of-fit test to see if all 5 colors of a certain candy appear in the same proportion in the population?
A) H1: p1 = p2 = p3 = p4 = p5 = .20.
B) H1: At least one proportion is not equal to .20.
C) H1: None of these proportions are equal.
D) None of these choices.
A) H1: p1 = p2 = p3 = p4 = p5 = .20.
B) H1: At least one proportion is not equal to .20.
C) H1: None of these proportions are equal.
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
27
Consider a multinomial experiment with 200 trials, where the outcome of each trial is classified into one of 5 categories.The number of degrees of freedom associated with the chi-squared goodness-of-fit test equals:
A) 195
B) 40
C) 5
D) 4
A) 195
B) 40
C) 5
D) 4

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
28
A(n) ____________________ experiment is like a binomial experiment except it contains two or more categories.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
29
How do you calculate the expected frequency for one cell in a goodness-of-fit test?
A) The expected frequency is equal to the proportion specified in H0 for that cell.
B) Use the total number of observations divided by the number of categories.
C) Multiply the specified proportion for that cell (found in H0) by the total sample size.
D) None of these choices.
A) The expected frequency is equal to the proportion specified in H0 for that cell.
B) Use the total number of observations divided by the number of categories.
C) Multiply the specified proportion for that cell (found in H0) by the total sample size.
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
30
To determine the critical values in the chi-squared distribution table, you need to know the:
A) sample size.
B) degrees of freedom
C) probability of Type II error.
D) All of these choices are true.
A) sample size.
B) degrees of freedom
C) probability of Type II error.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
31
The rule of five requires that the:
A) observed frequency for each cell must be at least 5.
B) degrees of freedom for the test must be at least 5.
C) expected frequency for each cell must be at least 5.
D) difference between the observed and expected frequency for each cell must be at least 5.
A) observed frequency for each cell must be at least 5.
B) degrees of freedom for the test must be at least 5.
C) expected frequency for each cell must be at least 5.
D) difference between the observed and expected frequency for each cell must be at least 5.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
32
A chi-squared goodness-of-fit test is always conducted as a(n):
A) lower-tail test.
B) upper-tail test.
C) two-tail test.
D) All of these choices are true.
A) lower-tail test.
B) upper-tail test.
C) two-tail test.
D) All of these choices are true.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following statements regarding the chi-squared distribution is true?
A) The chi-squared distribution is skewed to the right.
B) All values of the chi-squared distribution are greater than or equal to zero.
C) The critical region for a goodness-of-fit test with k categories is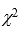 >
> 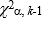 , where 11ef175b_3024_9000_8934_5ff5cbcb5071_TB7453_11 is the value of the test statistic.
, where 11ef175b_3024_9000_8934_5ff5cbcb5071_TB7453_11 is the value of the test statistic.
D) All of these choices are true.
A) The chi-squared distribution is skewed to the right.
B) All values of the chi-squared distribution are greater than or equal to zero.
C) The critical region for a goodness-of-fit test with k categories is
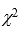 >
> 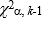 , where 11ef175b_3024_9000_8934_5ff5cbcb5071_TB7453_11 is the value of the test statistic.
, where 11ef175b_3024_9000_8934_5ff5cbcb5071_TB7453_11 is the value of the test statistic.D) All of these choices are true.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
34
If each element in a population is classified into one and only one of several categories, the population is:
A) normal.
B) multinomial.
C) chi-squared.
D) None of these choices.
A) normal.
B) multinomial.
C) chi-squared.
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
35
If the expected frequency ei for any cell i is less than 5, we should:
A) choose another sample with five or more observations.
B) use the normal distribution instead of the chi-squared distribution.
C) combine cells such that each observed frequency fi is 5 or more.
D) increase the degrees of freedom by 5.
A) choose another sample with five or more observations.
B) use the normal distribution instead of the chi-squared distribution.
C) combine cells such that each observed frequency fi is 5 or more.
D) increase the degrees of freedom by 5.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose the value of your chi-squared test statistic in a goodness-of-fit test is equal to 0.What do you conclude?
A) Reject H0.Conclude that at least one proportion is not equal to its specified value.
B) Fail to reject H0.Not enough evidence to say the proportions are different from what is listed in H0.
C) Not enough information; need the degrees of freedom for the test.
D) None of these choices.
A) Reject H0.Conclude that at least one proportion is not equal to its specified value.
B) Fail to reject H0.Not enough evidence to say the proportions are different from what is listed in H0.
C) Not enough information; need the degrees of freedom for the test.
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following is not a characteristic of a multinomial experiment?
A) The experiment consists of a fixed number of trials.
B) The outcome of each trial is classified into one of two possible categories.
C) The probability pi that the outcome will fall into cell i remains constant for each trial.
D) Each trial of the experiment is independent of the other trials.
A) The experiment consists of a fixed number of trials.
B) The outcome of each trial is classified into one of two possible categories.
C) The probability pi that the outcome will fall into cell i remains constant for each trial.
D) Each trial of the experiment is independent of the other trials.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
38
When k = 2 the ____________________ experiment is identical to the ____________________ experiment.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
39
A left tail area in the chi-squared distribution equals .99.For df = 8, the table value equals:
A) 20.090
B) 3.4895
C) 2.7326
D) 15.5073
A) 20.090
B) 3.4895
C) 2.7326
D) 15.5073

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
40
To determine whether data were drawn from a multinomial distribution with certain proportions, you use a:
A) chi-squared goodness-of-fit test.
B) chi-squared test of a contingency table.
C) chi-squared test for normality.
D) None of these choices.
A) chi-squared goodness-of-fit test.
B) chi-squared test of a contingency table.
C) chi-squared test for normality.
D) None of these choices.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
41
The alternative hypothesis of a goodness-of-fit test states that ____________________ of the proportions is not equal to its value specified in H0.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
42
A Deli proposes to serve 4 main Sandwiches.For planning purposes, the manager expects that the proportions of each that will be selected by her customers will be:
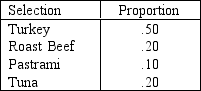 Of a random sample of 100 customers, 44 selected chicken, 24 selected roast beef, 13 selected Pastrami, and 10 selected tuna.Should the manager revise her estimates? Use = .01.
Of a random sample of 100 customers, 44 selected chicken, 24 selected roast beef, 13 selected Pastrami, and 10 selected tuna.Should the manager revise her estimates? Use = .01.
 Of a random sample of 100 customers, 44 selected chicken, 24 selected roast beef, 13 selected Pastrami, and 10 selected tuna.Should the manager revise her estimates? Use = .01.
Of a random sample of 100 customers, 44 selected chicken, 24 selected roast beef, 13 selected Pastrami, and 10 selected tuna.Should the manager revise her estimates? Use = .01. 
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
43
A cable company prepared four versions of a set of instructions for hooking up a TV.The company asked a sample of 1,600 people which one of the four forms was easiest to understand.In the sample, 425 people preferred Form A, 385 preferred Form B, 375 preferred Form C, and 415 preferred Form D.At the 5% level of significance, can one conclude that in the population there is a preferred form?

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
44
A calculus professor posted the following grade distribution guidelines for her elementary calculus class: 8% A, 35% B, 40% C, 12% D, and 5% F.A sample of 100 elementary statistics grades at the end of last semester showed 12 As, 30 Bs, 35 Cs, 15 Ds, and 8 Fs.Test at the 5% significance level to determine whether the actual grades deviate significantly from the posted grade distribution guidelines.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
45
Consumer panel preferences for three proposed Cafes are as follows:
 Use 0.05 level of significance and test to see if there is a preference among the three Cafes, according to the data.
Use 0.05 level of significance and test to see if there is a preference among the three Cafes, according to the data.
 Use 0.05 level of significance and test to see if there is a preference among the three Cafes, according to the data.
Use 0.05 level of significance and test to see if there is a preference among the three Cafes, according to the data.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
46
In 2011, Brand A MP3 Players had 45% of the market, Brand B had 35%, and Brand C had 20%.This year the makers of brand C launched a heavy advertising campaign.A random sample of electronic stores shows that of 10,000 MP3 Players sold, 4,350 were Brand A, 3,450 were Brand B, and 2,200 were Brand C.Has the market changed? Test at = .01.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
47
Explain what is meant by the rule of five and what you should do if this rule is not met.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
48
The chi-squared goodness-of-fit test compares the ____________________ frequencies in the table to the ____________________ frequencies based on the null hypothesis.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
49
If the expected frequencies and the observed frequencies are quite different, you are likely to ____________________ the null hypothesis.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
50
The rule of five states that in order to conduct the chi-squared goodness-of-fit test, the ____________________ value for each cell must be five or more.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
51
Consider a multinomial experiment involving 160 trials 4 categories (cells).The observed frequencies resulting from the experiment are shown in the accompanying table.
 Use the 10% significance level to test the hypotheses: H0: p1 = p2 = p3 = p4 = .25 vs.H1: At least one proportion differs from their specified values.
Use the 10% significance level to test the hypotheses: H0: p1 = p2 = p3 = p4 = .25 vs.H1: At least one proportion differs from their specified values.
 Use the 10% significance level to test the hypotheses: H0: p1 = p2 = p3 = p4 = .25 vs.H1: At least one proportion differs from their specified values.
Use the 10% significance level to test the hypotheses: H0: p1 = p2 = p3 = p4 = .25 vs.H1: At least one proportion differs from their specified values.
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
52
A test statistic that lies in the far right tail of the chi-squared distribution indicates you will ____________________ H0.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
53
To determine whether a single coin is fair, the coin was tossed 200 times.The observed frequencies with which each of the two sides of the coin turned up are recorded as 112 heads and 88 tails.Is the coin fair? Use a=.05

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
54
Consider a multinomial experiment involving 100 trials and 3 categories (cells).The observed frequencies resulting from the experiment are shown in the accompanying table.

Use the 5% significance level to test the hypotheses H0: p1 = .45, p2 = .30, p3 = .25 vs.H1: At least one proportion differs from their specified values.

Use the 5% significance level to test the hypotheses H0: p1 = .45, p2 = .30, p3 = .25 vs.H1: At least one proportion differs from their specified values.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
55
The rule of ____________________ states that in order to conduct the chi-squared goodness-of-fit test, the expected value for each cell must be ____________________ or more.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
56
The values of a chi-squared distribution are always ____________________ zero.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
57
In 2011, computers of Brand A controlled 25% of the market, Brand B 20%, Brand C 10%, and brand D 45%.In 2015, sample data was collected from many randomly selected stores throughout the country.Of the 1,200 computers sold, 280 were Brand A, 270 were Brand B, 90 were Brand C, and 560 were Brand D.Has the market changed since 2011? Test at the 1% significance level.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
58
In 2011, the student body of a state university in Alabama consists of 30% freshmen, 25% sophomores, 27% juniors, and 18% seniors.A sample of 400 students taken from the 2012 student body showed that there are 138 freshmen, 88 sophomores, 94 juniors, and 80 seniors.Test with 5% significance level to determine whether the student body proportions have changed.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
59
A chi-squared distribution has a shape that is ____________________.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
60
Five types of apples are displayed side by side in several supermarkets in the city of Miami.It was noted that in one day, 180 customers purchased apples.Of these, 30 picked type A, 40 picked type B, 25 picked type C, 35 picked type D, and 50 picked type E.In Miami, can you conclude at the 5% significance level that there is a preferred type of apples?

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
61
In the test of a contingency table, the observed cell frequencies must satisfy the rule of 5.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
62
In the test of a contingency table, the expected cell frequencies must satisfy the rule of 5.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
63
A chi-squared test of a contingency table is applied to a contingency table with 3 rows and 4 columns for two qualitative variables.The degrees of freedom for this test must be 12.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
64
The test statistic for the chi-squared test of a contingency table is the same as the test statistic for the goodness-of-fit test.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
65
Student Absenteeism
Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
-{Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies:

Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
-{Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies:


Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
66
A chi-squared test of a contingency table with 10 degrees of freedom results in a test statistic of 17.894.Using the chi-squared table, the most accurate statement that can be made about the p-value for this test is that .05 < p-value < .10.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
67
Student Absenteeism
Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
-{Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies: (n = 50)

Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
-{Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies: (n = 50)


Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
68
In a test of a contingency table, rejecting the null hypothesis concludes the variables are not independent.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
69
Student Absenteeism
Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
{Student Absenteeism Narrative} Review the previous results.What is the effect of decreasing the sample size?
Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
{Student Absenteeism Narrative} Review the previous results.What is the effect of decreasing the sample size?

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
70
In a goodness-of-fit test, H0 lists specific values for proportions and the test of a contingency table does not.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
71
To produce expected values for a test of a contingency table, you multiply estimated joint probabilities for each cell by the total sample size, n.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
72
A chi-squared test of a contingency table is applied to a contingency table with 4 rows and 4 columns for two qualitative variables.The degrees of freedom for this test must be 9.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
73
In a chi-squared test of a contingency table, the value of the test statistic was 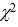 = 15.652, and the critical value at = .025 was 11.1433.Thus, we must reject the null hypothesis at = .025.
= 15.652, and the critical value at = .025 was 11.1433.Thus, we must reject the null hypothesis at = .025.
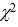 = 15.652, and the critical value at = .025 was 11.1433.Thus, we must reject the null hypothesis at = .025.
= 15.652, and the critical value at = .025 was 11.1433.Thus, we must reject the null hypothesis at = .025. 
Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
74
A chi-squared test of a contingency table with 6 degrees of freedom results in a test statistic of 13.25.Using the chi-squared table, the most accurate statement that can be made about the p-value for this test is that p-value is greater than .025 but smaller than .05.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
75
If two events A and B are independent, the P(A and B) = P(A) + P(B).

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
76
Student Absenteeism
Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
-{Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies: (n = 100)

Consider a multinomial experiment involving n = 200 students of a large high school.The attendance department recorded the number of students who were absent during the weekdays.The null hypothesis to be tested is: H0: p1 = .10, p2 = .25, p3 = .30, p4 = .20, p5 = .15.
-{Student Absenteeism Narrative} Test the hypothesis at the 5% level of significance with the following frequencies: (n = 100)


Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
77
To calculate the expected values in a test of a contingency table, you assume that the null hypothesis is true.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
78
Sales Volumes
A telemarketer makes five calls per day.A sample of 200 days gives the frequencies of sales volumes listed below:
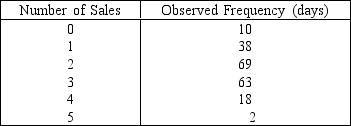 Assume the population is binomial distribution with a probability of purchase p equal to .50.
Assume the population is binomial distribution with a probability of purchase p equal to .50.
{Sales Volumes Narrative} Compute the expected frequencies for x = 0, 1, 2, 3, 4, and 5 by using the binomial probability function or the binomial tables.Combine categories if necessary to satisfy the rule of five.
A telemarketer makes five calls per day.A sample of 200 days gives the frequencies of sales volumes listed below:
 Assume the population is binomial distribution with a probability of purchase p equal to .50.
Assume the population is binomial distribution with a probability of purchase p equal to .50.{Sales Volumes Narrative} Compute the expected frequencies for x = 0, 1, 2, 3, 4, and 5 by using the binomial probability function or the binomial tables.Combine categories if necessary to satisfy the rule of five.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
79
Sales Volumes
A telemarketer makes five calls per day.A sample of 200 days gives the frequencies of sales volumes listed below:
 Assume the population is binomial distribution with a probability of purchase p equal to .50.
Assume the population is binomial distribution with a probability of purchase p equal to .50.
-{Sales Volumes Narrative} Should the assumption of a binomial distribution be rejected at the 5% significance level?
A telemarketer makes five calls per day.A sample of 200 days gives the frequencies of sales volumes listed below:
 Assume the population is binomial distribution with a probability of purchase p equal to .50.
Assume the population is binomial distribution with a probability of purchase p equal to .50.-{Sales Volumes Narrative} Should the assumption of a binomial distribution be rejected at the 5% significance level?

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck
80
The expected frequency for the cell in row i and column j is the row i total plus the row j total, all divided by n.

Unlock Deck
Unlock for access to all 175 flashcards in this deck.
Unlock Deck
k this deck


