Deck 10: Discriminant Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/57
Play
Full screen (f)
Deck 10: Discriminant Analysis
1
The goal of discriminant analysis is
A) to develop a model to predict new dependent values.
B) the develop a rule for predicting to what group a new observation is most likely to belong.
C) to develop a rule for predicting how independent variable values predict dependent values.
D) none of these.
A) to develop a model to predict new dependent values.
B) the develop a rule for predicting to what group a new observation is most likely to belong.
C) to develop a rule for predicting how independent variable values predict dependent values.
D) none of these.
B
2
Which of the following is not true regarding discriminant analysis?
A) The classification rule translates discriminant scores into group membership.
B) Discriminant analysis is based on discrete or categorical dependent variables.
C) The classification rule selected perfectly classifies the data used to derive the classification rule.
D) The confusion matrix summarizes classification results.
A) The classification rule translates discriminant scores into group membership.
B) Discriminant analysis is based on discrete or categorical dependent variables.
C) The classification rule selected perfectly classifies the data used to derive the classification rule.
D) The confusion matrix summarizes classification results.
C
3
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the verbal test score value of the group centroid for group 2?
A) 683.8
B) 654.2
C) 610.7
D) 605.7
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the verbal test score value of the group centroid for group 2?
A) 683.8
B) 654.2
C) 610.7
D) 605.7
605.7
4
In discriminant analysis the averages for the independent variables for a group define the
A) centroid.
B) median.
C) mode.
D) central tendency.
A) centroid.
B) median.
C) mode.
D) central tendency.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
5
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the verbal test score value of the group centroid for group 1?
A) 683.8
B) 654.2
C) 610.7
D) 605.7
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the verbal test score value of the group centroid for group 1?
A) 683.8
B) 654.2
C) 610.7
D) 605.7

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
6
Given the following confusion matrix what is the correct classification rate?
A) 9/13 = 69%
B) 10/14 = 86%
C) 19/25 = 76%
D) 6/19 = 32%
A) 9/13 = 69%
B) 10/14 = 86%
C) 19/25 = 76%
D) 6/19 = 32%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
7
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What percentage of the observations is classified incorrectly?
A) 90%
B) 80%
C) 85%
D) 15%
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What percentage of the observations is classified incorrectly?
A) 90%
B) 80%
C) 85%
D) 15%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
8
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. How many observations are classified correctly?
A) 11
B) 9
C) 17
D) 20
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. How many observations are classified correctly?
A) 11
B) 9
C) 17
D) 20

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
9
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What number of observations is classified incorrectly?
A) 3
B) 9
C) 17
D) 20
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What number of observations is classified incorrectly?
A) 3
B) 9
C) 17
D) 20

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
10
If using the regression tool for two-group discriminant analysis, in the regression dialog box, the Input Y-Range entry corresponds to
A) the Group values.
B) the independent variable values.
C) the predictor variable values.
D) (b) and (c) are both correct
A) the Group values.
B) the independent variable values.
C) the predictor variable values.
D) (b) and (c) are both correct

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
11
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What percentage of the observations is classified correctly?
A) 90%
B) 80%
C) 85%
D) 100%
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What percentage of the observations is classified correctly?
A) 90%
B) 80%
C) 85%
D) 100%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
12
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. How would you compute the centroids for the two (2) groups?
A) compute the average for cells C4:C13, C13:C23, D4:D13 and D13:D23
B) perform regression on cells C4:C13, C13:C23, D4:D13 and D13:D23
C) compute the average for cells C4:C23, D4:D23
D) use regression with cells C4:C23, D4:D23 as the independent variables and B4:B23 as the dependent variable.
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. How would you compute the centroids for the two (2) groups?
A) compute the average for cells C4:C13, C13:C23, D4:D13 and D13:D23
B) perform regression on cells C4:C13, C13:C23, D4:D13 and D13:D23
C) compute the average for cells C4:C23, D4:D23
D) use regression with cells C4:C23, D4:D23 as the independent variables and B4:B23 as the dependent variable.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
13
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 2?
A) 683.8
B) 654.2
C) 610.7
D) 605.7
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 2?
A) 683.8
B) 654.2
C) 610.7
D) 605.7

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
14
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 1?
A) 683.8
B) 654.2
C) 610.7
D) 605.7
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 1?
A) 683.8
B) 654.2
C) 610.7
D) 605.7

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
15
Discriminant analysis (DA) differs from most other predictive statistical methods because the dependent variable is
A) continuous
B) random
C) stochastic
D) discrete
A) continuous
B) random
C) stochastic
D) discrete

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
16
In a two-group discriminant analysis problem using regression, why is the midpoint cut-off value used to determine group classification?
A) Because the value minimizes the absolute misclassification error.
B) Because the value minimizes the probability of misclassification error.
C) Because the value represents an equal division between the groups.
D) Because the value incorporates problem specific knowledge.
A) Because the value minimizes the absolute misclassification error.
B) Because the value minimizes the probability of misclassification error.
C) Because the value represents an equal division between the groups.
D) Because the value incorporates problem specific knowledge.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
17
The regression approach can be used in the two-group discriminant analysis problem because
A) the data are not normally distributed.
B) the R2 statistic is not very meaningful.
C) the regression equation can generate a discriminant score.
D) it scales to the k-group problem easily.
A) the data are not normally distributed.
B) the R2 statistic is not very meaningful.
C) the regression equation can generate a discriminant score.
D) it scales to the k-group problem easily.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
18
If using the regression tool for two-group discriminant analysis, in the regression dialog box, the Input X-Range entry corresponds to
A) the Group values.
B) the independent variable values.
C) the predicted variable values.
D) the fitted variable values.
A) the Group values.
B) the independent variable values.
C) the predicted variable values.
D) the fitted variable values.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following goodness-of-fit measures is used for discriminant analysis problems?
A) R2
B) multiple R2
C) adjusted R2
D) none of these
A) R2
B) multiple R2
C) adjusted R2
D) none of these

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following best describes a group centroid?
A) A set of averages for the independent variables for the group.
B) The average for all independent variables across all the groups.
C) The center values for the independent variables for the group.
D) The center value among all independent variables across all the groups.
A) A set of averages for the independent variables for the group.
B) The average for all independent variables across all the groups.
C) The center values for the independent variables for the group.
D) The center value among all independent variables across all the groups.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
21
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. The straight line distance between two points (X1, Y1) and (X2, Y2) is calculated as
A) X1 ? Y1 + X2 ? Y2
B) (X1 ? X2)2 + (Y1 ? Y2)2
C)
D)
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. The straight line distance between two points (X1, Y1) and (X2, Y2) is calculated as
A) X1 ? Y1 + X2 ? Y2
B) (X1 ? X2)2 + (Y1 ? Y2)2
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
22
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the quantitative test score value of the group centroid for group 1?
A) 697.71
B) 647.86
C) 587.67
D) 650.43
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the quantitative test score value of the group centroid for group 1?
A) 697.71
B) 647.86
C) 587.67
D) 650.43

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
23
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What formula is entered in cell F4 of the spreadsheet to compute the Predicted Group for the first student?
A) =IF(E4?$E$26,2,1)
B) =IF(E4?$E$26,1,2)
C) =IF(E4>$E$24,1,0)
D) =IF(E4?$E$24,1,2)
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What formula is entered in cell F4 of the spreadsheet to compute the Predicted Group for the first student?
A) =IF(E4?$E$26,2,1)
B) =IF(E4?$E$26,1,2)
C) =IF(E4>$E$24,1,0)
D) =IF(E4?$E$24,1,2)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
24
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is small. This means that
A) The observation is likely to be classified incorrectly
B) The observation is likely to be classified correctly
C) The observation is unlikely to be classified
D) The observation should be deleted from the data set
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is small. This means that
A) The observation is likely to be classified incorrectly
B) The observation is likely to be classified correctly
C) The observation is unlikely to be classified
D) The observation should be deleted from the data set

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
25
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified incorrectly?
A) 5%
B) 15%
C) 95%
D) 90%
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified incorrectly?
A) 5%
B) 15%
C) 95%
D) 90%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
26
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Based on the regression output, what is the discriminant score for a student with a quantitative score of 635 and a verbal score of 570?
A) 1.72 ? discriminant score ? 1.73
B) 2.02 ? discriminant score ? 2.03
C) 3.04 ? discriminant score ? 3.05
D) 6.12 ? discriminant score ? 6.14
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Based on the regression output, what is the discriminant score for a student with a quantitative score of 635 and a verbal score of 570?
A) 1.72 ? discriminant score ? 1.73
B) 2.02 ? discriminant score ? 2.03
C) 3.04 ? discriminant score ? 3.05
D) 6.12 ? discriminant score ? 6.14

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
27
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. The university has received applications from several new students and would like to predict which group they would fall into. What is the discriminant score for a student with a Quantitative score of 686 and a Verbal score of 601. Use five (5) significant figures in your coefficients.
A) 1.29 ? discriminant score ? 1.30
B) 1.69 ? discriminant score ? 1.70
C) 2.69 ? discriminant score ? 2.70
D) 6.05 ? discriminant score ? 6.06
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. The university has received applications from several new students and would like to predict which group they would fall into. What is the discriminant score for a student with a Quantitative score of 686 and a Verbal score of 601. Use five (5) significant figures in your coefficients.
A) 1.29 ? discriminant score ? 1.30
B) 1.69 ? discriminant score ? 1.70
C) 2.69 ? discriminant score ? 2.70
D) 6.05 ? discriminant score ? 6.06

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
28
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified correctly?
A) 100%
B) 85.71%
C) 95%
D) 90%
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified correctly?
A) 100%
B) 85.71%
C) 95%
D) 90%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
29
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the quantitative test score value of the group centroid for group 2?
A) 697.71
B) 647.86
C) 587.67
D) 650.43
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the quantitative test score value of the group centroid for group 2?
A) 697.71
B) 647.86
C) 587.67
D) 650.43

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
30
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is big and positive. This means that
A) The observation is likely to be classified correctly to group 2
B) The observation is likely to be classified correctly to group 1
C) The observation is likely to be classified incorrectly to group 2
D) The observation is likely to be classified incorrectly to group 1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is big and positive. This means that
A) The observation is likely to be classified correctly to group 2
B) The observation is likely to be classified correctly to group 1
C) The observation is likely to be classified incorrectly to group 2
D) The observation is likely to be classified incorrectly to group 1

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
31
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the verbal test score value of the group centroid for group 3?
A) 697.71
B) 647.86
C) 587.67
D) 605.17
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the verbal test score value of the group centroid for group 3?
A) 697.71
B) 647.86
C) 587.67
D) 605.17

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
32
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the cut-off value (cell E26) for this data using the mid-point cut-off method?
A) 1.189
B) 1.499
C) 1.809
D) 2.000
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the cut-off value (cell E26) for this data using the mid-point cut-off method?
A) 1.189
B) 1.499
C) 1.809
D) 2.000

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
33
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What formula is entered in cell E26 of the spreadsheet to determine the Cut-off Value, assuming that the admissions officer wants to minimize the probability of overlap between the groups?
A) =E24+E25/2
B) =(E24+E25)/2
C) =AVERAGE(E4:E13)
D) =AVERAGE(E14:E23)
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What formula is entered in cell E26 of the spreadsheet to determine the Cut-off Value, assuming that the admissions officer wants to minimize the probability of overlap between the groups?
A) =E24+E25/2
B) =(E24+E25)/2
C) =AVERAGE(E4:E13)
D) =AVERAGE(E14:E23)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
34
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is big and negative. This means that
A) The observation is likely to be classified correctly to group 2
B) The observation is likely to be classified correctly to group 1
C) The observation is likely to be classified incorrectly to group 2
D) The observation is likely to be classified incorrectly to group 1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is big and negative. This means that
A) The observation is likely to be classified correctly to group 2
B) The observation is likely to be classified correctly to group 1
C) The observation is likely to be classified incorrectly to group 2
D) The observation is likely to be classified incorrectly to group 1

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
35
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the straight line distance between (6,4) and (2,9)?
A) 3.20
B) 6.40
C) 9
D) 41
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What is the straight line distance between (6,4) and (2,9)?
A) 3.20
B) 6.40
C) 9
D) 41

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
36
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What number of observations is classified incorrectly?
A) 19
B) 20
C) 7
D) 1
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What number of observations is classified incorrectly?
A) 19
B) 20
C) 7
D) 1

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What number of observations is classified correctly?
A) 19
B) 20
C) 7
D) 8
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What number of observations is classified correctly?
A) 19
B) 20
C) 7
D) 8

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
38
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What formula is entered in cell E4 and copied to cells E5:E25 of the spreadsheet?
A) = 7.452402 + 0.00694*C4 + 0.00232*D4
B) = 7.452402 ? 0.00694*C4 ? 0.00232*D4
C) = 1.157926 + 0.001545*C4 + 0.01297*D4
D) = 7.452402 ? 0.00694*D4 ? 0.00232*C4
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).



-Refer to Exhibit 10.1. What formula is entered in cell E4 and copied to cells E5:E25 of the spreadsheet?
A) = 7.452402 + 0.00694*C4 + 0.00232*D4
B) = 7.452402 ? 0.00694*C4 ? 0.00232*D4
C) = 1.157926 + 0.001545*C4 + 0.01297*D4
D) = 7.452402 ? 0.00694*D4 ? 0.00232*C4

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
39
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. Based on the analysis presented in the spreadsheet, what percentage of the observations were correctly classified?
A) 80%
B) 85%
C) 95%
D) 100%
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. Based on the analysis presented in the spreadsheet, what percentage of the observations were correctly classified?
A) 80%
B) 85%
C) 95%
D) 100%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
40
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the verbal test score value of the group centroid for group 1?
A) 697.71
B) 647.86
C) 587.67
D) 650.43
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).


-Refer to Exhibit 10.2. What is the verbal test score value of the group centroid for group 1?
A) 697.71
B) 647.86
C) 587.67
D) 650.43

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
41
The term serves which of the following purposes?
A) Accounts for prior probabilities of group membership.
B) Reduces the overlap area of the classification rules.
C) Ensures the data follow an exponential distribution.
D) Removes the midpoint information from the classification rules.
A) Accounts for prior probabilities of group membership.
B) Reduces the overlap area of the classification rules.
C) Ensures the data follow an exponential distribution.
D) Removes the midpoint information from the classification rules.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
42
Exhibit 10.6
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.
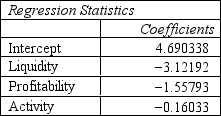
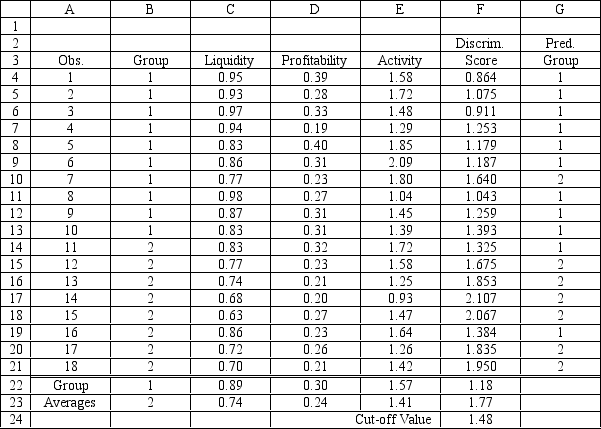

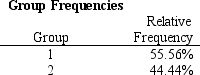
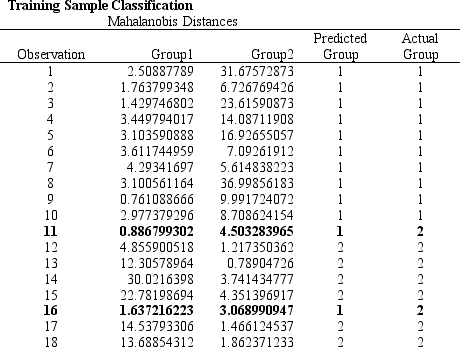
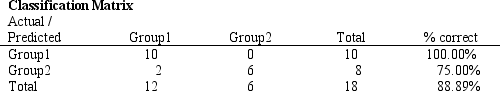
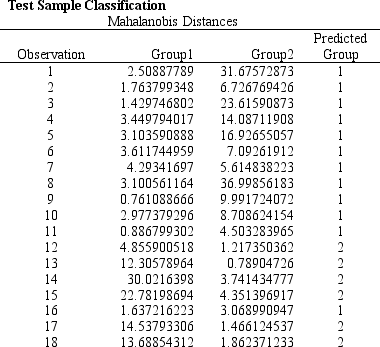
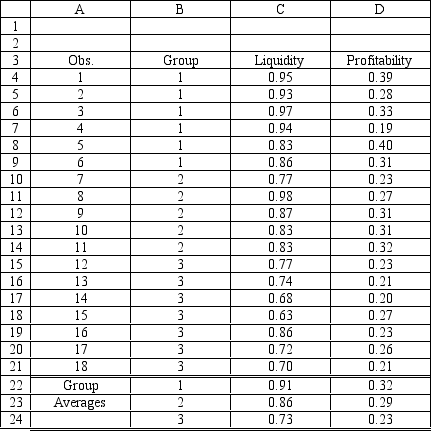
Refer to Exhibit 10.6. What formulas should go in cells C22:D23, E4:G24, and F24 of the spreadsheet?
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.





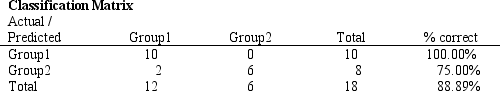

Refer to Exhibit 10.6. What formulas should go in cells C22:D23, E4:G24, and F24 of the spreadsheet?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 10.7
The information below is used for the following questions.
An investor wants to classify companies as being a High Risk Investment, Group 1, a Medium Risk Investment, Group 2, or a Low Risk Investment, Group 3. He has gathered Liquidity, Profitability data on 18 companies he has invested in and produced the following spreadsheet. The following Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated.

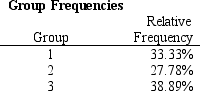
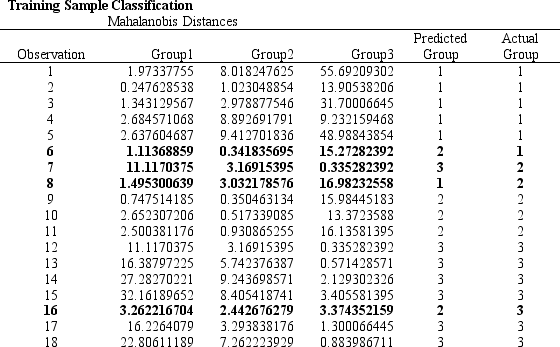
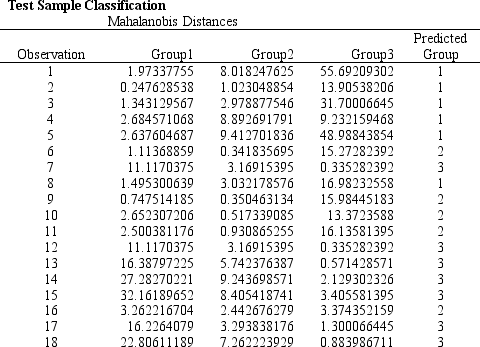
Refer to Exhibit 10.7. What formulas should go in cells C22:D24 of the spreadsheet?
The information below is used for the following questions.
An investor wants to classify companies as being a High Risk Investment, Group 1, a Medium Risk Investment, Group 2, or a Low Risk Investment, Group 3. He has gathered Liquidity, Profitability data on 18 companies he has invested in and produced the following spreadsheet. The following Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated.





Refer to Exhibit 10.7. What formulas should go in cells C22:D24 of the spreadsheet?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
44
Refer to Exhibit 10.3. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.
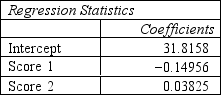
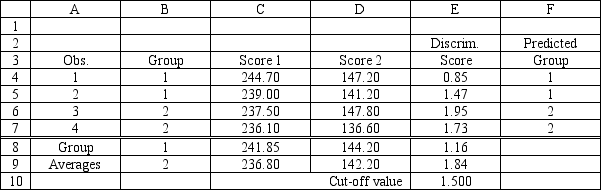

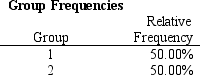
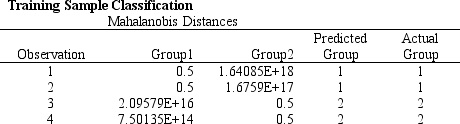

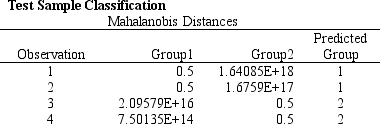
Refer to Exhibit 10.4. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







Refer to Exhibit 10.4. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
45
Which of the following statements is true concerning multiple discriminant analysis distance measures?
A) A data point should fall nearest the centroid of the group to which it belongs.
B) A pure distance measure ignores data variance which can influence classification accuracy.
C) Mahalanobis distance measure accounts for differences in covariance between independent variables.
D) All of these are true.
A) A data point should fall nearest the centroid of the group to which it belongs.
B) A pure distance measure ignores data variance which can influence classification accuracy.
C) Mahalanobis distance measure accounts for differences in covariance between independent variables.
D) All of these are true.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
46
Exhibit 10.7
The information below is used for the following questions.
An investor wants to classify companies as being a High Risk Investment, Group 1, a Medium Risk Investment, Group 2, or a Low Risk Investment, Group 3. He has gathered Liquidity, Profitability data on 18 companies he has invested in and produced the following spreadsheet. The following Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated.





Refer to Exhibit 10.7. Based on the 18 observations in the model complete the following confusion/classification matrix.

The information below is used for the following questions.
An investor wants to classify companies as being a High Risk Investment, Group 1, a Medium Risk Investment, Group 2, or a Low Risk Investment, Group 3. He has gathered Liquidity, Profitability data on 18 companies he has invested in and produced the following spreadsheet. The following Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated.





Refer to Exhibit 10.7. Based on the 18 observations in the model complete the following confusion/classification matrix.


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
47
Exhibit 10.3
The information below is used for the following questions.
A loan officer wants to determine if people will be late in making loan payments. She has information of 18 current loans including the applicants income, level of assets and whether or not the person has been late on payments. She has performed an analysis on the data using Regression tool in Excel and the Risk Solver Platform (RSP). The data for the problem and the relevant output are shown below.
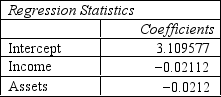
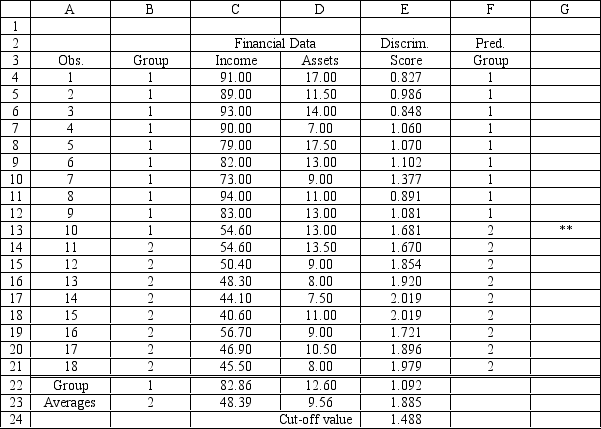

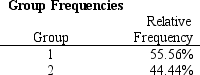
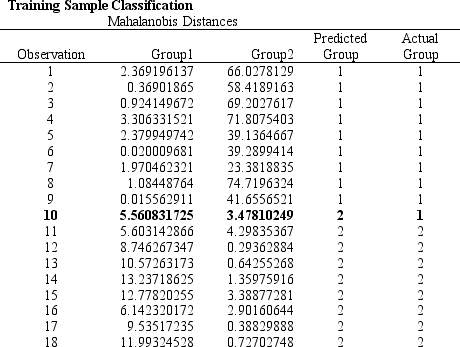
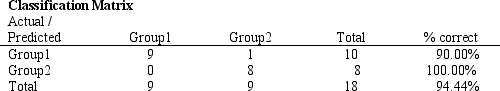
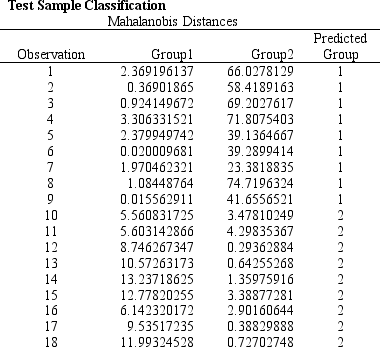
Refer to Exhibit 10.3. Compute the discriminant score and predicted group for someone with an income of 65 and assets of 11.
The information below is used for the following questions.
A loan officer wants to determine if people will be late in making loan payments. She has information of 18 current loans including the applicants income, level of assets and whether or not the person has been late on payments. She has performed an analysis on the data using Regression tool in Excel and the Risk Solver Platform (RSP). The data for the problem and the relevant output are shown below.





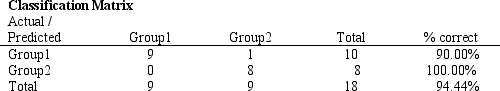

Refer to Exhibit 10.3. Compute the discriminant score and predicted group for someone with an income of 65 and assets of 11.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
48
Multiple discriminant analysis moves away from a regression approach to using a measure of distance. Which of the following characterizes the use of a distance function?
A) Each data value's distance from the origin will align with the appropriate group regression line.
B) A data value will fall nearest to the centroid point of its group.
C) The distance measure accounts for the variance of the group data as well as the group centroid.
D) Neither (b) nor (c) characterize the distance measure.
A) Each data value's distance from the origin will align with the appropriate group regression line.
B) A data value will fall nearest to the centroid point of its group.
C) The distance measure accounts for the variance of the group data as well as the group centroid.
D) Neither (b) nor (c) characterize the distance measure.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
49
Exhibit 10.6
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.



-Refer to Exhibit 10.6. Based on the 20 observations and the RSP output, what percentage of the observations are correctly classified?
A) 80.00%
B) 88.89%
C) 75.25%
D) 95.14%
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.



-Refer to Exhibit 10.6. Based on the 20 observations and the RSP output, what percentage of the observations are correctly classified?
A) 80.00%
B) 88.89%
C) 75.25%
D) 95.14%

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
50
Exhibit 10.3
The information below is used for the following questions.
A loan officer wants to determine if people will be late in making loan payments. She has information of 18 current loans including the applicants income, level of assets and whether or not the person has been late on payments. She has performed an analysis on the data using Regression tool in Excel and the Risk Solver Platform (RSP). The data for the problem and the relevant output are shown below.





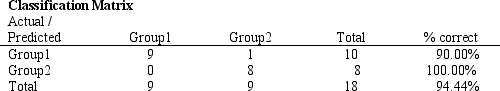

Refer to Exhibit 10.3. What formulas should go in cells C22:D23 and E4:F24 of the spreadsheet?
The information below is used for the following questions.
A loan officer wants to determine if people will be late in making loan payments. She has information of 18 current loans including the applicants income, level of assets and whether or not the person has been late on payments. She has performed an analysis on the data using Regression tool in Excel and the Risk Solver Platform (RSP). The data for the problem and the relevant output are shown below.





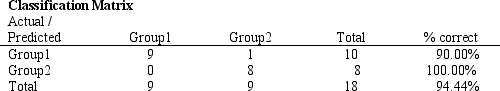

Refer to Exhibit 10.3. What formulas should go in cells C22:D23 and E4:F24 of the spreadsheet?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
51
Refer to Exhibit 10.3. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







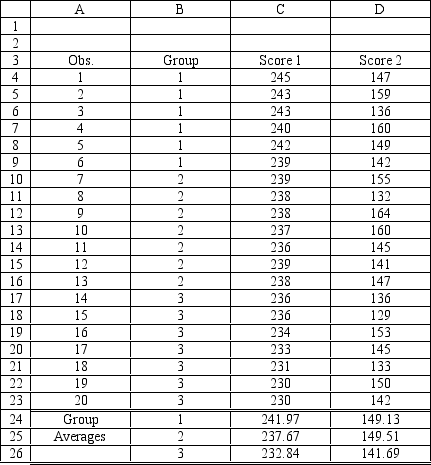
Refer to Exhibit 10.4. What formulas should go in cells C8:D9 and E4:G10 of the spreadsheet?
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







Refer to Exhibit 10.4. What formulas should go in cells C8:D9 and E4:G10 of the spreadsheet?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
52
Exhibit 10.5
The information below is used for the following questions.
A counselor wants to classify people as belonging to one of three groups based on two scores. The counselor has collected data on twenty people who are known to be in one of the three groups. The data for the problem are in the following spreadsheet. Output generated using Risk Solver Platform (RSP) is also included.

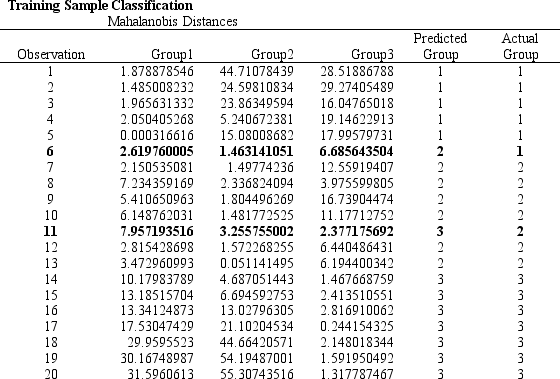
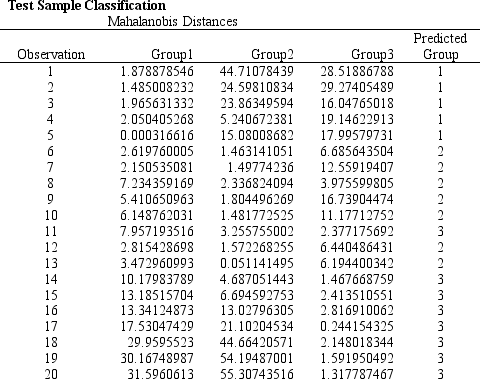
Refer to Exhibit 10.5. Based on the 20 observations in the model complete the following confusion/classification matrix.

The information below is used for the following questions.
A counselor wants to classify people as belonging to one of three groups based on two scores. The counselor has collected data on twenty people who are known to be in one of the three groups. The data for the problem are in the following spreadsheet. Output generated using Risk Solver Platform (RSP) is also included.





Refer to Exhibit 10.5. Based on the 20 observations in the model complete the following confusion/classification matrix.


Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
53
Exhibit 10.5
The information below is used for the following questions.
A counselor wants to classify people as belonging to one of three groups based on two scores. The counselor has collected data on twenty people who are known to be in one of the three groups. The data for the problem are in the following spreadsheet. Output generated using Risk Solver Platform (RSP) is also included.





Refer to Exhibit 10.5. What formulas should go in cells C24:D26 of the spreadsheet?
The information below is used for the following questions.
A counselor wants to classify people as belonging to one of three groups based on two scores. The counselor has collected data on twenty people who are known to be in one of the three groups. The data for the problem are in the following spreadsheet. Output generated using Risk Solver Platform (RSP) is also included.





Refer to Exhibit 10.5. What formulas should go in cells C24:D26 of the spreadsheet?

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
54
Refer to Exhibit 10.3. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







Refer to Exhibit 10.4. Compute the discriminant score and predicted group for someone with Score 1 of 242 and Score 2 of 142.
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







Refer to Exhibit 10.4. Compute the discriminant score and predicted group for someone with Score 1 of 242 and Score 2 of 142.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
55
Refer to Exhibit 10.3. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







Refer to Exhibit 10.4. Compute the discriminant score and predicted group for someone with Score 1 of 238 and Score 2 of 140.
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.







Refer to Exhibit 10.4. Compute the discriminant score and predicted group for someone with Score 1 of 238 and Score 2 of 140.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
56
Exhibit 10.6
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.





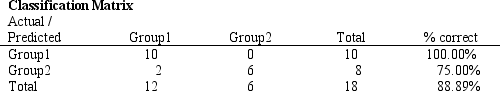

Refer to Exhibit 10.6. Compute the discriminant score and predicted group for a company with Liquidity = 0.91, Profitability = 0.32 and Activity = 1.39.
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.





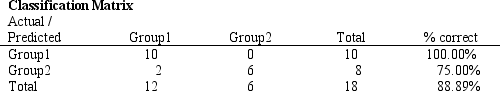

Refer to Exhibit 10.6. Compute the discriminant score and predicted group for a company with Liquidity = 0.91, Profitability = 0.32 and Activity = 1.39.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
57
Exhibit 10.6
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.





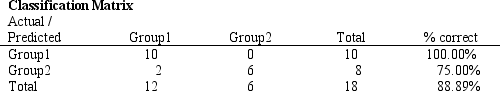

Refer to Exhibit 10.6. Compute the discriminant score and predicted group for a company with Liquidity = 0.80, Profitability = 0.27 and Activity = 1.55.
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.





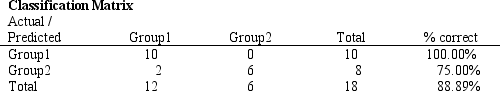

Refer to Exhibit 10.6. Compute the discriminant score and predicted group for a company with Liquidity = 0.80, Profitability = 0.27 and Activity = 1.55.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck


