Exam 10: Discriminant Analysis
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
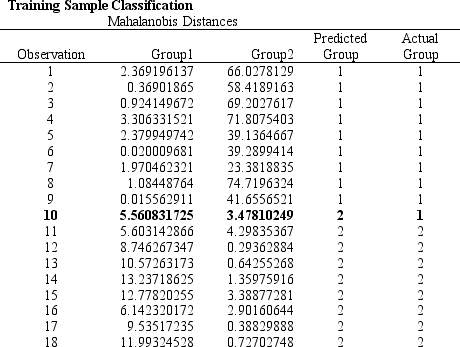
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).

 Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%
Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%  -Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is big and positive. This means that
-Refer to Exhibit 10.1. Suppose that for a given observation, the difference between Mahalanobis distances between group 1 and 2 (G1-G2) is big and positive. This means that
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
A
Exhibit 10.6
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.
Coefficients Intercept 4.690338 Liquidity -3.12192 Profitability -1.55793 Activity -0.16033
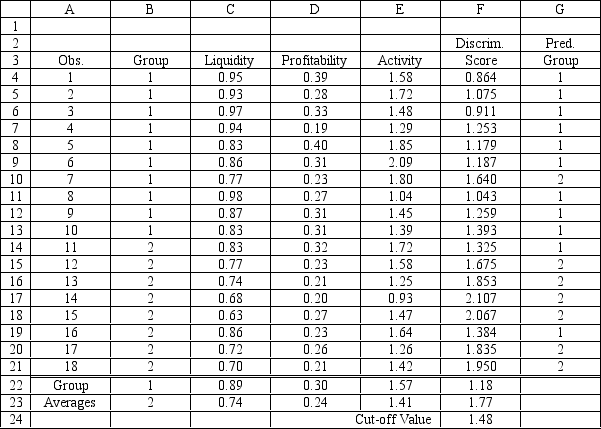 Group 1 2 3 1 0.893 0.302 1.569 2 074125 074125 1.4875
Relative Group Frequency 1 55.56\% 2 44.44\%
Group 1 2 3 1 0.893 0.302 1.569 2 074125 074125 1.4875
Relative Group Frequency 1 55.56\% 2 44.44\% 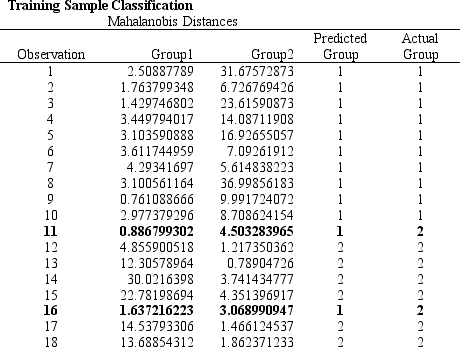 Actual/ Predicted Group1 Group2 Total \% correct Group1 10 0 10 100.00\% Group2 2 6 8 75.00\% Total 12 6 18 88.89\%
Actual/ Predicted Group1 Group2 Total \% correct Group1 10 0 10 100.00\% Group2 2 6 8 75.00\% Total 12 6 18 88.89\%
 -Refer to Exhibit 10.6. Based on the 20 observations and the RSP output, what percentage of the observations are correctly classified?
-Refer to Exhibit 10.6. Based on the 20 observations and the RSP output, what percentage of the observations are correctly classified?
Free
(Multiple Choice)
4.8/5  (26)
(26)
Correct Answer:
B
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).

 Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%
Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%  -Refer to Exhibit 10.1. Based on the regression output, what is the discriminant score for a student with a quantitative score of 635 and a verbal score of 570?
-Refer to Exhibit 10.1. Based on the regression output, what is the discriminant score for a student with a quantitative score of 635 and a verbal score of 570?
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
A
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).

 Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%
Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%  -Refer to Exhibit 10.1. What formula is entered in cell E26 of the spreadsheet to determine the Cut-off Value, assuming that the admissions officer wants to minimize the probability of overlap between the groups?
-Refer to Exhibit 10.1. What formula is entered in cell E26 of the spreadsheet to determine the Cut-off Value, assuming that the admissions officer wants to minimize the probability of overlap between the groups?
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).
 Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%
Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%  Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified correctly?
Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified correctly?
(Multiple Choice)
4.8/5  (32)
(32)
Multiple discriminant analysis moves away from a regression approach to using a measure of distance. Which of the following characterizes the use of a distance function?
(Multiple Choice)
4.9/5  (37)
(37)
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).

 Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%
Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%  -Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 2?
-Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 2?
(Multiple Choice)
4.8/5  (30)
(30)
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).
 Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%
Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%  Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. What number of observations is classified correctly?
Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. What number of observations is classified correctly?
(Multiple Choice)
4.8/5  (28)
(28)
Exhibit 10.6
The information below is used for the following questions.
An investor wants to classify companies as being either a good investment, Group 1, or a poor investment, Group 2. He has gathered Liquidity, Profitability and Activity data on 18 companies he has invested in and run a regression analysis. Discriminant Analysis output using Risk Solver Platform (RSP) has also been generated. The data for the problem and the relevant output are shown below.
Coefficients Intercept 4.690338 Liquidity -3.12192 Profitability -1.55793 Activity -0.16033
 Group 1 2 3 1 0.893 0.302 1.569 2 074125 074125 1.4875
Relative Group Frequency 1 55.56\% 2 44.44\%
Group 1 2 3 1 0.893 0.302 1.569 2 074125 074125 1.4875
Relative Group Frequency 1 55.56\% 2 44.44\%  Actual/ Predicted Group1 Group2 Total \% correct Group1 10 0 10 100.00\% Group2 2 6 8 75.00\% Total 12 6 18 88.89\%
Actual/ Predicted Group1 Group2 Total \% correct Group1 10 0 10 100.00\% Group2 2 6 8 75.00\% Total 12 6 18 88.89\%
 -Refer to Exhibit 10.6. Compute the discriminant score and predicted group for a company with Liquidity = 0.80, Profitability = 0.27 and Activity = 1.55.
-Refer to Exhibit 10.6. Compute the discriminant score and predicted group for a company with Liquidity = 0.80, Profitability = 0.27 and Activity = 1.55.
(Essay)
4.8/5  (39)
(39)
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).

 Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%
Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%  -Refer to Exhibit 10.1. What is the verbal test score value of the group centroid for group 2?
-Refer to Exhibit 10.1. What is the verbal test score value of the group centroid for group 2?
(Multiple Choice)
4.9/5  (34)
(34)
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).
 Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%
Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%  Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. What number of observations is classified incorrectly?
Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. What number of observations is classified incorrectly?
(Multiple Choice)
4.8/5  (20)
(20)
Exhibit 10.3
The information below is used for the following questions.
A loan officer wants to determine if people will be late in making loan payments. She has information of 18 current loans including the applicants income, level of assets and whether or not the person has been late on payments. She has performed an analysis on the data using Regression tool in Excel and the Risk Solver Platform (RSP). The data for the problem and the relevant output are shown below.
Regression Slatisties Coefficients Intercept 3.109577 Income -0.02112 Assets -0.0212 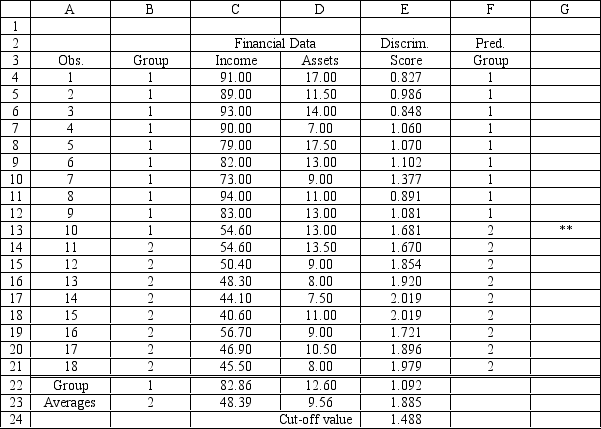 Group 1 2 1 82.86 12.6 2 483875 05625
Relative Group Frequency 1 55.56\% 2 44.44\%
Group 1 2 1 82.86 12.6 2 483875 05625
Relative Group Frequency 1 55.56\% 2 44.44\%
 Actual/ Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 0 8 8 100.00\% Total 0 0 18 04.44\%
Actual/ Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 0 8 8 100.00\% Total 0 0 18 04.44\%
 -Refer to Exhibit 10.3. What formulas should go in cells C22:D23 and E4:F24 of the spreadsheet?
-Refer to Exhibit 10.3. What formulas should go in cells C22:D23 and E4:F24 of the spreadsheet?
(Essay)
4.8/5  (38)
(38)
Which of the following goodness-of-fit measures is used for discriminant analysis problems?
(Multiple Choice)
4.9/5  (28)
(28)
Exhibit 10.2
The following questions are based on the problem description, spreadsheet, and the Risk Solver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful (Group 1), marginally successful (Group 2) or not-successful (Group 3) in their graduate studies. The officer has data on 20 current students, 7 successful (Group 1), 6 marginally successful (Group 2) and 7 not successful (Group 3).
 Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%
Group Quantitative Verbal 1 697.7142857 650.4285714 2 647.8571429 630.7142857 3 5876666667 6051666667
Relative Group Frequency 1 35.00\% 2 35.00\% 3 3000\%  Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified incorrectly?
Actual / Predicted Group1 Group2 Group3 Total \% correct Group1 6 1 0 7 85.71\% Group2 0 7 0 7 100.00\% Group3 0 0 6 6 100.00\% Total 6 8 6 20 95.00\%
-Refer to Exhibit 10.2. Based on the RSP output, what percentage of observations is classified incorrectly?
(Multiple Choice)
4.7/5  (38)
(38)
Refer to Exhibit 10.3. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
ANS:
a.
94.44%
b.
5.56%
c.
90%
d.
100%
PTS: 1
Exhibit 10.4
The information below is used for the following questions.
A manager wants to classify people as belonging to one of two groups based on two scores. The manager has collected data on four current employees and has performed a regression analysis on the data. The data for the problem and the relevant output are shown below.
Coefficients Intercept 31.8158 Score 1 -0.14956 Score 2 0.03825
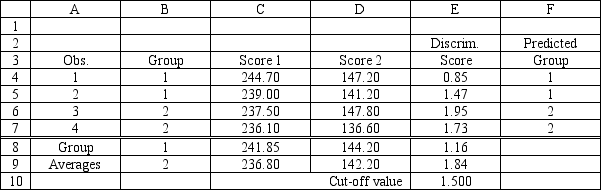 Group 1 2 1 241.85 144.2 2 236.8 1422
Relative Group Frequency 1 50.00\% 2 50.00\%
Predicted Actual Observation Group 1 Group2 Group Group 1 0.5 1.64085+18 1 1 2 0.5 1.6759+17 1 1 3 2.09579+16 0.5 2 2 4 750135+14 05 2 2
Actual/ Predicted Group1 Group2 Total \% correct Group1 2 0 2 100.00\% Group2 0 2 2 100.00\% Total 2 2 4 100.00\%
Predicted Observation Group 1 Group2 Group 1 0.5 1.64085+18 1 2 0.5 1.6759+17 1 3 2.09579+16 0.5 2 4 750135+14 05 2
-Refer to Exhibit 10.4. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
Group 1 2 1 241.85 144.2 2 236.8 1422
Relative Group Frequency 1 50.00\% 2 50.00\%
Predicted Actual Observation Group 1 Group2 Group Group 1 0.5 1.64085+18 1 1 2 0.5 1.6759+17 1 1 3 2.09579+16 0.5 2 2 4 750135+14 05 2 2
Actual/ Predicted Group1 Group2 Total \% correct Group1 2 0 2 100.00\% Group2 0 2 2 100.00\% Total 2 2 4 100.00\%
Predicted Observation Group 1 Group2 Group 1 0.5 1.64085+18 1 2 0.5 1.6759+17 1 3 2.09579+16 0.5 2 4 750135+14 05 2
-Refer to Exhibit 10.4. What is the percentage of observations:
a.
Correctly classified to a Group?
b.
Incorrectly classified to a Group?
c.
Correctly classified to Group 1?
d.
Correctly classified to Group 2?
(Essay)
4.9/5  (29)
(29)
In a two-group discriminant analysis problem using regression, why is the midpoint cut-off value used to determine group classification?
(Multiple Choice)
4.9/5  (33)
(33)
Exhibit 10.1
The following questions are based on the problem description, regression results, and the RiskSolver Platform (RSP) Discriminant Analysis report below.
A college admissions officer wants to evaluate graduate school applicants based on their GMAT scores, verbal and quantitative. Students are classified as either successful or not-successful in their graduate studies. The officer has data on 20 current students, ten of whom are doing very well (Group 1) and ten who are not (Group 2).

 Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%
Group Quantitative Verbal 1 683.8 654.2 2 6107 6057
Actual / Predicted Group1 Group2 Total \% correct Group1 9 1 10 90.00\% Group2 2 8 10 80.00\% Tnta1 11 0 20 850\%\%  -Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 1?
-Refer to Exhibit 10.1. What is the quantitative test score value of the group centroid for group 1?
(Multiple Choice)
5.0/5  (40)
(40)
Showing 1 - 20 of 57
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)