Deck 20: Model Building
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 20: Model Building
1
In explaining the income earned by university graduates, which of the following independent variables is best represented by an indicator variable in a regression model?
A) Grade point average.
B) Gender
C) Number of years since graduating from high school.
D) Age
A) Grade point average.
B) Gender
C) Number of years since graduating from high school.
D) Age
B
2
The model 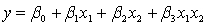 +
+ 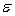 is referred to as a:
is referred to as a:
A) first-order model with two predictor variables with no interaction.
B) first-order model with two predictor variables with interaction.
C) second-order model with three predictor variables with no interaction.
D) second-order model with three predictor variables with interaction.
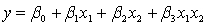 +
+ 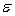 is referred to as a:
is referred to as a:A) first-order model with two predictor variables with no interaction.
B) first-order model with two predictor variables with interaction.
C) second-order model with three predictor variables with no interaction.
D) second-order model with three predictor variables with interaction.
B
3
Which of the following best describes Stepwise regression?
A) Stepwise regression may involve adding one independent variable at a time.
B) Stepwise regression may involve deleting one independent variable at a time.
C) Stepwise regression may involve dividing one independent variable at a time.
D) Stepwise regression may involve adding or deleting one independent variable at a time.
A) Stepwise regression may involve adding one independent variable at a time.
B) Stepwise regression may involve deleting one independent variable at a time.
C) Stepwise regression may involve dividing one independent variable at a time.
D) Stepwise regression may involve adding or deleting one independent variable at a time.
D
4
In explaining starting salaries for graduates of computer science programs, which of the following independent variables would not be adequately represented with a dummy variable?
A) Grade point average.
B) Gender.
C) Race.
D) Marital status.
A) Grade point average.
B) Gender.
C) Race.
D) Marital status.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following describes the numbers that an indicator variable can have in a regression model?
A) 0 and 1
B) 1 and 2
C) 0, 1 and 2
D) None of these choices are correct.
A) 0 and 1
B) 1 and 2
C) 0, 1 and 2
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
The model 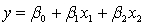 +
+ 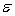 is referred to as a:
is referred to as a:
A) first-order model with one predictor variable.
B) first-order model with two predictor variables.
C) second-order model with one predictor variable.
D) second-order model with two predictor variables.
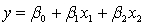 +
+ 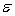 is referred to as a:
is referred to as a:A) first-order model with one predictor variable.
B) first-order model with two predictor variables.
C) second-order model with one predictor variable.
D) second-order model with two predictor variables.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is another name for a dummy variable?
A) Independent variable
B) Dependent variable
C) Indicator variable
D) Y variable
A) Independent variable
B) Dependent variable
C) Indicator variable
D) Y variable

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
The graph of the model  is shaped like a straight line going upwards.
is shaped like a straight line going upwards.
 is shaped like a straight line going upwards.
is shaped like a straight line going upwards. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that the estimated regression equation for 200 business graduates is ŷ = 20 000 + 2000x + 1500I,
Where y is the starting salary, x is the grade point average and I is an indicator variable that takes the value of 1 if the student is a computer information systems major and 0 if not. A business administration major graduate with a grade point average of 4 would have an average starting salary of:
A) $20 000.
B) $26 000.
C) $29 500.
D) $28 000.
Where y is the starting salary, x is the grade point average and I is an indicator variable that takes the value of 1 if the student is a computer information systems major and 0 if not. A business administration major graduate with a grade point average of 4 would have an average starting salary of:
A) $20 000.
B) $26 000.
C) $29 500.
D) $28 000.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
In general, to represent a categorical independent variable that has m possible categories, which of the following is the number of dummy variables that can be used in the regression model?
A) (m + 1) dummy variables.
B) m dummy variables.
C) (1 − m) dummy variables.
D) (m - 1) dummy variables.
A) (m + 1) dummy variables.
B) m dummy variables.
C) (1 − m) dummy variables.
D) (m - 1) dummy variables.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
In a stepwise regression procedure, if two independent variables are highly correlated, then:
A) both variables will enter the equation.
B) only one variable will enter the equation.
C) neither variable will enter the equation.
D) None of these choices are correct.
A) both variables will enter the equation.
B) only one variable will enter the equation.
C) neither variable will enter the equation.
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose that the sample regression equation of a model is  . If we examine the relationship between and y for four different values of , we observe that the four equations produced differ only in the intercept term.
. If we examine the relationship between and y for four different values of , we observe that the four equations produced differ only in the intercept term.
 . If we examine the relationship between and y for four different values of , we observe that the four equations produced differ only in the intercept term.
. If we examine the relationship between and y for four different values of , we observe that the four equations produced differ only in the intercept term. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
When we plot x versus y, the graph of the model 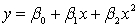 +
+ 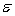 is shaped like a:
is shaped like a:
A) straight line going upwards.
B) straight line going downwards.
C) circle.
D) parabola.
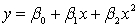 +
+ 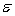 is shaped like a:
is shaped like a:A) straight line going upwards.
B) straight line going downwards.
C) circle.
D) parabola.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
In explaining the amount of money spent on children's clothes each month, which of the following independent variables is best represented with an indicator variable?
A) Age.
B) Height.
C) Gender.
D) Weight.
A) Age.
B) Height.
C) Gender.
D) Weight.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that the sample regression line of a first order model is  . If we examine the relationship between y and for four different values of , we observe that the:
. If we examine the relationship between y and for four different values of , we observe that the:
A) effect of x on y remains the same no matter what the value of x .
B) effect of x on y remains the same no matter what the value of x .
C) only difference in the four equations produced is the coefficient of x .
D) None of these choices are correct.
 . If we examine the relationship between y and for four different values of , we observe that the:
. If we examine the relationship between y and for four different values of , we observe that the:A) effect of x on y remains the same no matter what the value of x .
B) effect of x on y remains the same no matter what the value of x .
C) only difference in the four equations produced is the coefficient of x .
D) None of these choices are correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
In explaining students' test scores, which of the following independent variables would not be adequately represented by an indicator variable?
A) Gender
B) Cultural background
C) Number of hours studying for the test
D) Marital status
A) Gender
B) Cultural background
C) Number of hours studying for the test
D) Marital status

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
For the regression equation  , which combination of and , respectively, results in the largest average value of y?
, which combination of and , respectively, results in the largest average value of y?
A) 3 and 5.
B) 5 and 3.
C) 6 and 3.
D) 3 and 6.
 , which combination of and , respectively, results in the largest average value of y?
, which combination of and , respectively, results in the largest average value of y?A) 3 and 5.
B) 5 and 3.
C) 6 and 3.
D) 3 and 6.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is not an advantage of multiple regression as compared with analysis of variance?
A) Multiple regression can be used to estimate the relationship between the dependent variable and independent variables.
B) Multiple regression handles qualitative variables better than analysis of variance.
C) Multiple regression handles problems with more than two independent variables better than analysis of variance.
D) All of the above are advantages of multiple regression as compared with analysis of variance.
A) Multiple regression can be used to estimate the relationship between the dependent variable and independent variables.
B) Multiple regression handles qualitative variables better than analysis of variance.
C) Multiple regression handles problems with more than two independent variables better than analysis of variance.
D) All of the above are advantages of multiple regression as compared with analysis of variance.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose that the sample regression equation of a model is  . If we examine the relationship between and y for three different values of , we observe that the:
. If we examine the relationship between and y for three different values of , we observe that the:
A) three equations produced differ only in the intercept.
B) coefficient of remains unchanged.
C) coefficient of varies.
D) three equations produced differ not only in the intercept term but the coefficient of , also varies.
 . If we examine the relationship between and y for three different values of , we observe that the:
. If we examine the relationship between and y for three different values of , we observe that the:A) three equations produced differ only in the intercept.
B) coefficient of remains unchanged.
C) coefficient of varies.
D) three equations produced differ not only in the intercept term but the coefficient of , also varies.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
The following model 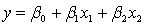 +
+ 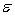 is used whenever the statistician believes that, on average, y is linearly related to:
is used whenever the statistician believes that, on average, y is linearly related to:
A)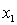 , and the predictor variables do not interact.
, and the predictor variables do not interact.
B)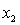 , and the predictor variables do not interact.
, and the predictor variables do not interact.
C)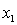 and the predictor variables do not interact or to
and the predictor variables do not interact or to 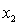 , and the predictor variables do not interact.
, and the predictor variables do not interact.
D)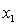 and the predictor variables do not interact and to
and the predictor variables do not interact and to 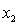 , and the predictor variables do not interact.
, and the predictor variables do not interact.
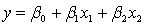 +
+ 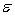 is used whenever the statistician believes that, on average, y is linearly related to:
is used whenever the statistician believes that, on average, y is linearly related to:A)
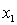 , and the predictor variables do not interact.
, and the predictor variables do not interact.B)
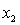 , and the predictor variables do not interact.
, and the predictor variables do not interact.C)
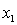 and the predictor variables do not interact or to
and the predictor variables do not interact or to 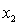 , and the predictor variables do not interact.
, and the predictor variables do not interact.D)
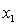 and the predictor variables do not interact and to
and the predictor variables do not interact and to 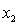 , and the predictor variables do not interact.
, and the predictor variables do not interact.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Stepwise regression is an iterative procedure that can only add one independent variable at a time.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
The model 
is referred to as a first-order model with two predictor variables with no interaction.

is referred to as a first-order model with two predictor variables with no interaction.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
In the first-order model ŷ = 8 + 3x1 +5x2, a unit increase in 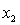 , while holding
, while holding 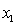 constant, increases the value of
constant, increases the value of 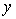 on average by 3 units.
on average by 3 units.
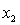 , while holding
, while holding 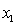 constant, increases the value of
constant, increases the value of 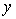 on average by 3 units.
on average by 3 units.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
In the first-order model 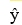 = 60 + 40x1 -10x2 + 5x1x2, a unit increase in x1, while holding x2 constant at 1, increases the value of on average by 45 units.
= 60 + 40x1 -10x2 + 5x1x2, a unit increase in x1, while holding x2 constant at 1, increases the value of on average by 45 units.
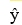 = 60 + 40x1 -10x2 + 5x1x2, a unit increase in x1, while holding x2 constant at 1, increases the value of on average by 45 units.
= 60 + 40x1 -10x2 + 5x1x2, a unit increase in x1, while holding x2 constant at 1, increases the value of on average by 45 units. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
In a first-order model with two predictors, 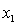 and
and 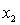 , an interaction term may be used when the relationship between the dependent variable
, an interaction term may be used when the relationship between the dependent variable 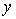 and the predictor variables is linear.
and the predictor variables is linear.
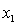 and
and 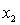 , an interaction term may be used when the relationship between the dependent variable
, an interaction term may be used when the relationship between the dependent variable 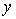 and the predictor variables is linear.
and the predictor variables is linear.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Regression analysis allows the statistics practitioner to use mathematical models to realistically describe relationships between the dependent variable and independent variables.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose that the sample regression line of a first-order model is  . If we examine the relationship between y and for three different values of , we observe that the effect of on remains the same no matter what the value of .
. If we examine the relationship between y and for three different values of , we observe that the effect of on remains the same no matter what the value of .
 . If we examine the relationship between y and for three different values of , we observe that the effect of on remains the same no matter what the value of .
. If we examine the relationship between y and for three different values of , we observe that the effect of on remains the same no matter what the value of . 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
In general, to represent a nominal independent variable that has n possible categories, we would create n dummy variables.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
In explaining the amount of money spent on children's toys during Christmas each year, the independent variable 'gender' is best represented by a dummy variable.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
In a stepwise regression procedure, if two independent variables are highly correlated, then one variable usually eliminates the second variable.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Stepwise regression is especially useful when there are many independent variables.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
In the first-order model 
, a unit increase in , while holding constant at a value of 3, decreases the value of on average by 3 units.

, a unit increase in , while holding constant at a value of 3, decreases the value of on average by 3 units.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
In the first-order regression model ŷ = 12 + 6x1 +8x2 + 4x1x2, a unit increase in x1 increases the value of 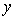 on average by 6 units.
on average by 6 units.
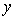 on average by 6 units.
on average by 6 units.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
In the first-order model 
, a unit increase in , while holding constant at a value of 2, decreases the value of on average by 8 units.

, a unit increase in , while holding constant at a value of 2, decreases the value of on average by 8 units.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose that the sample regression equation of a model is 
. If we examine the relationship between y and for = 1, 2 and 3, we observe that the three equations produced not only differ in the intercept term, but the coefficient of also varies.

. If we examine the relationship between y and for = 1, 2 and 3, we observe that the three equations produced not only differ in the intercept term, but the coefficient of also varies.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
In regression analysis, indicator variables may be used as independent variables.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
The model  is used whenever the statistician believes that, on average, is linearly related to and , and the predictor variables do not interact.
is used whenever the statistician believes that, on average, is linearly related to and , and the predictor variables do not interact.
 is used whenever the statistician believes that, on average, is linearly related to and , and the predictor variables do not interact.
is used whenever the statistician believes that, on average, is linearly related to and , and the predictor variables do not interact. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
The model y = 0 + 1x + 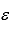 is referred to as a simple linear regression model.
is referred to as a simple linear regression model.
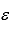 is referred to as a simple linear regression model.
is referred to as a simple linear regression model. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
The model y = 0 + 1x + 2x2 + … + pxp + 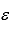 is referred to as a polynomial model with p predictor variables.
is referred to as a polynomial model with p predictor variables.
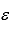 is referred to as a polynomial model with p predictor variables.
is referred to as a polynomial model with p predictor variables. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
The model  is referred to as a second-order model with two predictor variables with interaction.
is referred to as a second-order model with two predictor variables with interaction.
 is referred to as a second-order model with two predictor variables with interaction.
is referred to as a second-order model with two predictor variables with interaction. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the following data for two variables, x and y. Use Excel to develop an estimated regression equation of the form ? = b0 +b1x + b2x2..

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the following data for two variables, x and y, where x is the age of a particular make of car
and y is the selling price, in thousands of dollars. Use Excel to test whether the population slope is positive, at the 1% level of significance.
Use Excel to test whether the population slope is positive, at the 1% level of significance.
and y is the selling price, in thousands of dollars.
 Use Excel to test whether the population slope is positive, at the 1% level of significance.
Use Excel to test whether the population slope is positive, at the 1% level of significance.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the following data for two variables, x and y. Use the model in 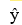 = 66.799 -7.307x + 0.324x2 to predict the value of y when x = 10.
= 66.799 -7.307x + 0.324x2 to predict the value of y when x = 10.
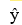 = 66.799 -7.307x + 0.324x2 to predict the value of y when x = 10.
= 66.799 -7.307x + 0.324x2 to predict the value of y when x = 10. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
A regression analysis was performed to study the relationship between a dependent variable and four independent variables. The following information was obtained:
r2 = 0.95, SSR = 9800, n = 50.
ANOVA Test the overall validity of the model at the 5% significance level.
Test the overall validity of the model at the 5% significance level.
r2 = 0.95, SSR = 9800, n = 50.
ANOVA
 Test the overall validity of the model at the 5% significance level.
Test the overall validity of the model at the 5% significance level.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the following data for two variables, x and y. Use Excel to determine whether there is sufficient evidence at the 1% significance level to infer that the relationship between y, x and in 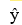 = 66.799 -7.307x + 0.324x2 is significant.
= 66.799 -7.307x + 0.324x2 is significant.
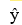 = 66.799 -7.307x + 0.324x2 is significant.
= 66.799 -7.307x + 0.324x2 is significant. 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
In regression analysis, we can use 11 indicator variables to represent 12 months of the year.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
A regression analysis was performed to study the relationship between a dependent variable and four independent variables. The following information was obtained:
r2 = 0.95, SSR = 9800, n = 50.
Create the ANOVA table.
r2 = 0.95, SSR = 9800, n = 50.
Create the ANOVA table.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following data for two variables, x and y.  Use Excel to find the coefficient of determination. What does this statistic tell you about this curvilinear model?
Use Excel to find the coefficient of determination. What does this statistic tell you about this curvilinear model?
 Use Excel to find the coefficient of determination. What does this statistic tell you about this curvilinear model?
Use Excel to find the coefficient of determination. What does this statistic tell you about this curvilinear model?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
An avid football fan was in the process of examining the factors that determine the success or failure of football teams. He noticed that teams with many rookies and teams with many veterans seem to do quite poorly. To further analyse his beliefs, he took a random sample of 20 teams and proposed a second-order model with one independent variable. The selected model is: 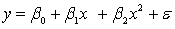 .
.
where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS: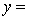
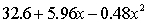
 S = 16.1 R-Sq = 43.9%.
S = 16.1 R-Sq = 43.9%.
ANALYSIS OF VARIANCE Test to determine at the 10% significance level if the linear term should be retained.
Test to determine at the 10% significance level if the linear term should be retained.
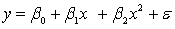 .
.where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS:
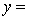
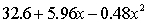
 S = 16.1 R-Sq = 43.9%.
S = 16.1 R-Sq = 43.9%.ANALYSIS OF VARIANCE
 Test to determine at the 10% significance level if the linear term should be retained.
Test to determine at the 10% significance level if the linear term should be retained.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 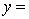
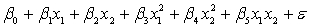 .
.
Where:
y = number of annual fatalities per shire.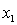 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 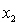 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS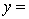
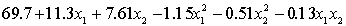 .
. 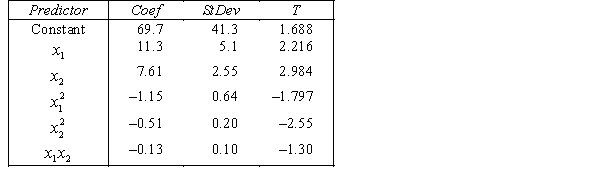 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the number of fatalities?
Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the number of fatalities?
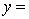
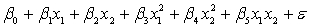 .
.Where:
y = number of annual fatalities per shire.
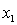 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 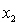 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
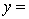
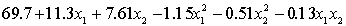 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the number of fatalities?
Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the number of fatalities?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
A regression analysis involving 40 observations and five independent variables revealed that the total variation in the dependent variable y is 1080 and that the mean square for error is 30.
Create the ANOVA table.
Create the ANOVA table.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the following data for two variables, x and y.  Use Excel to find the coefficient of determination. What does this statistic tell you about this simple linear model?
Use Excel to find the coefficient of determination. What does this statistic tell you about this simple linear model?
 Use Excel to find the coefficient of determination. What does this statistic tell you about this simple linear model?
Use Excel to find the coefficient of determination. What does this statistic tell you about this simple linear model?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
An indicator variable (also called a dummy variable) is a variable that can assume either one of two values (usually 0 and 1), where one value represents the existence of a certain condition, and the other value indicates that the condition does not hold.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the following data for two variables, x and y.  Use Excel to develop a scatter diagram for the data. Does the scatter diagram suggest an estimated regression equation of the form ŷ = b0 +b1x + b2x2? Explain.
Use Excel to develop a scatter diagram for the data. Does the scatter diagram suggest an estimated regression equation of the form ŷ = b0 +b1x + b2x2? Explain.
 Use Excel to develop a scatter diagram for the data. Does the scatter diagram suggest an estimated regression equation of the form ŷ = b0 +b1x + b2x2? Explain.
Use Excel to develop a scatter diagram for the data. Does the scatter diagram suggest an estimated regression equation of the form ŷ = b0 +b1x + b2x2? Explain.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
An avid football fan was in the process of examining the factors that determine the success or failure of football teams. He noticed that teams with many rookies and teams with many veterans seem to do quite poorly. To further analyse his beliefs, he took a random sample of 20 teams and proposed a second-order model with one independent variable. The selected model is: 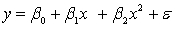 .
.
where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS: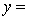
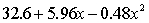
 S = 16.1 R-Sq = 43.9%.
S = 16.1 R-Sq = 43.9%.
ANALYSIS OF VARIANCE What is the coefficient of determination? Explain what this statistic tells you about the model.
What is the coefficient of determination? Explain what this statistic tells you about the model.
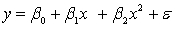 .
.where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS:
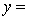
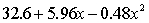
 S = 16.1 R-Sq = 43.9%.
S = 16.1 R-Sq = 43.9%.ANALYSIS OF VARIANCE
 What is the coefficient of determination? Explain what this statistic tells you about the model.
What is the coefficient of determination? Explain what this statistic tells you about the model.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
We interpret the coefficients in a multiple regression model by holding all variables in the model constant.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
An avid football fan was in the process of examining the factors that determine the success or failure of football teams. He noticed that teams with many rookies and teams with many veterans seem to do quite poorly. To further analyse his beliefs, he took a random sample of 20 teams and proposed a second-order model with one independent variable. The selected model is: .
where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS: S = 16.1 R-Sq = 43.9%.
ANALYSIS OF VARIANCE Do these results allow us to conclude at the 5% significance level that the model is useful in predicting the team's winning percentage?
where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS: S = 16.1 R-Sq = 43.9%.
ANALYSIS OF VARIANCE Do these results allow us to conclude at the 5% significance level that the model is useful in predicting the team's winning percentage?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
A regression analysis involving 40 observations and five independent variables revealed that the total variation in the dependent variable y is 1080 and that the mean square for error is 30.  Test the significance of the overall equation at the 5% level of significance.
Test the significance of the overall equation at the 5% level of significance.
 Test the significance of the overall equation at the 5% level of significance.
Test the significance of the overall equation at the 5% level of significance.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
An avid football fan was in the process of examining the factors that determine the success or failure of football teams. He noticed that teams with many rookies and teams with many veterans seem to do quite poorly. To further analyse his beliefs, he took a random sample of 20 teams and proposed a second-order model with one independent variable. The selected model is: 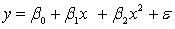 .
.
where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS: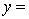
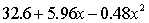
 S = 16.1 R-Sq = 43.9%.
S = 16.1 R-Sq = 43.9%.
ANALYSIS OF VARIANCE Test to determine at the 10% significance level whether the
Test to determine at the 10% significance level whether the 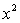 term should be retained.
term should be retained.
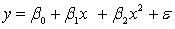 .
.where
y = winning team's percentage.
x = average years of professional experience.
The computer output is shown below:
THE REGRESSION EQUATION IS:
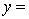
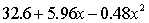
 S = 16.1 R-Sq = 43.9%.
S = 16.1 R-Sq = 43.9%.ANALYSIS OF VARIANCE
 Test to determine at the 10% significance level whether the
Test to determine at the 10% significance level whether the 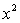 term should be retained.
term should be retained.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Consider the following data for two variables, x and y, where x is the age of a particular make of car
and y is the selling price, in thousands of dollars. a. Use Excel to develop an estimated regression equation of the form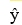 = b0 +b1x.
= b0 +b1x.
b. Interpret the intercept.
c. Interpret the slope.
and y is the selling price, in thousands of dollars. a. Use Excel to develop an estimated regression equation of the form
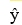 = b0 +b1x.
= b0 +b1x.b. Interpret the intercept.
c. Interpret the slope.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 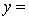
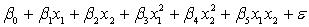 .
.
Where:
y = number of annual fatalities per shire.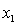 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 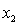 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS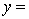
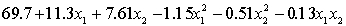 .
. 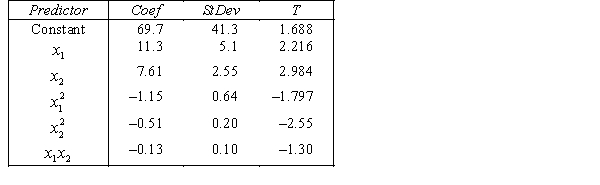 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 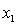 term should be retained in the model.
term should be retained in the model.
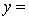
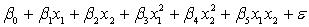 .
.Where:
y = number of annual fatalities per shire.
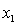 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 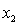 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
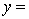
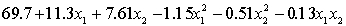 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 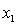 term should be retained in the model.
term should be retained in the model.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
An economist is analysing the incomes of professionals (physicians, dentists and lawyers). He realises that an important factor is the number of years of experience. However, he wants to know if there are differences among the three professional groups. He takes a random sample of 125 professionals and estimates the multiple regression model: 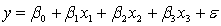 .
.
where
y
= annual income (in $1000).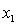 = years of experience.
= years of experience. 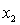 = 1 if physician.
= 1 if physician.
= 0 if not.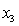 = 1 if dentist.
= 1 if dentist.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS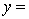
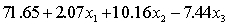 .
. 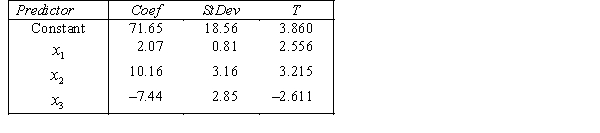 S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
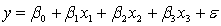 .
.where
y
= annual income (in $1000).
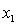 = years of experience.
= years of experience. 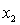 = 1 if physician.
= 1 if physician.= 0 if not.
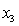 = 1 if dentist.
= 1 if dentist.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
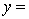
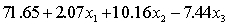 .
.  S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 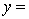
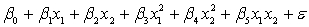 .
.
Where:
y = number of annual fatalities per shire.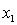 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 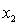 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS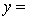
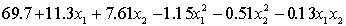 .
. 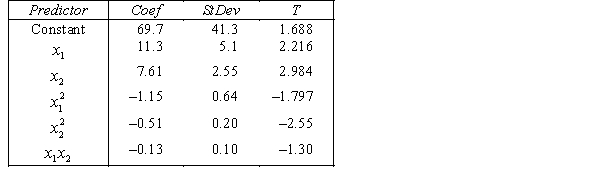 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 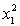 term should be retained in the model.
term should be retained in the model.
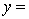
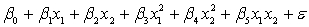 .
.Where:
y = number of annual fatalities per shire.
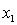 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 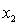 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
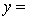
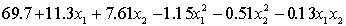 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 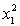 term should be retained in the model.
term should be retained in the model.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 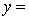
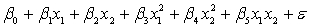 .
.
Where:
y = number of annual fatalities per shire.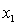 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 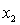 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS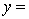
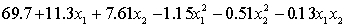 .
. 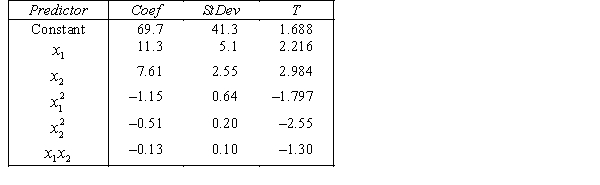 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 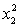 term should be retained in the model.
term should be retained in the model.
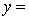
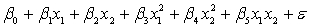 .
.Where:
y = number of annual fatalities per shire.
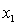 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 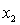 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
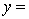
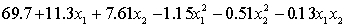 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 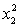 term should be retained in the model.
term should be retained in the model.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
An economist is in the process of developing a model to predict the price of gold. She believes that the two most important variables are the price of a barrel of oil 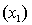 and the interest rate
and the interest rate 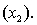 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 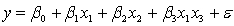 .
.
A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS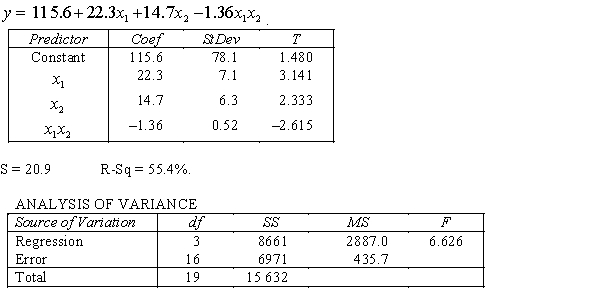 Is there sufficient evidence at the 1% significance level to conclude that the price of a barrel of oil and the price of gold are linearly related?
Is there sufficient evidence at the 1% significance level to conclude that the price of a barrel of oil and the price of gold are linearly related?
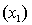 and the interest rate
and the interest rate 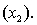 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 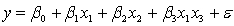 .
.A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS
 Is there sufficient evidence at the 1% significance level to conclude that the price of a barrel of oil and the price of gold are linearly related?
Is there sufficient evidence at the 1% significance level to conclude that the price of a barrel of oil and the price of gold are linearly related?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 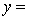
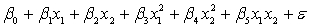 .
.
Where:
y = number of annual fatalities per shire.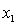 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 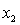 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS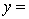
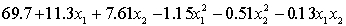 .
. 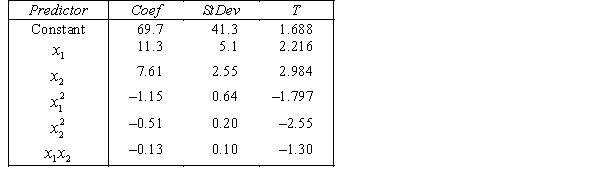 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 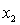 term should be retained in the model.
term should be retained in the model.
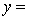
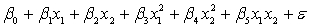 .
.Where:
y = number of annual fatalities per shire.
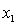 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 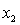 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
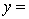
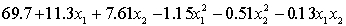 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 Test at the 1% significance level to determine whether the
Test at the 1% significance level to determine whether the 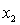 term should be retained in the model.
term should be retained in the model.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
A professor of accounting wanted to develop a multiple regression model to predict the students' grades in her fourth-year accounting course. She decides that the two most important factors are the student's grade point average (GPA) in the first three years and the student's major. She proposes the model: 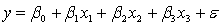 .
.
where
y
= fourth-year accounting course mark (out of 100).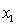 = GPA in first three years (range 0 to 12).
= GPA in first three years (range 0 to 12). 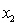 = 1 if student's major is accounting.
= 1 if student's major is accounting.
= 0 if not.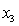 = 1 if student's major is finance.
= 1 if student's major is finance.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS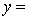
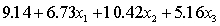 .
. 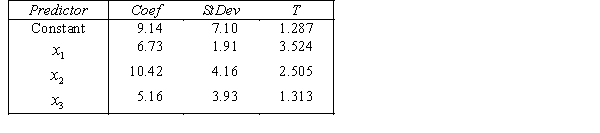 S = 15.0 R-Sq = 44.2%.
S = 15.0 R-Sq = 44.2%.  Do these results allow us to conclude at the 1% significance level that on average finance majors outperform those whose majors are not accounting or finance?
Do these results allow us to conclude at the 1% significance level that on average finance majors outperform those whose majors are not accounting or finance?
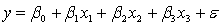 .
.where
y
= fourth-year accounting course mark (out of 100).
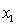 = GPA in first three years (range 0 to 12).
= GPA in first three years (range 0 to 12). 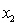 = 1 if student's major is accounting.
= 1 if student's major is accounting.= 0 if not.
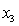 = 1 if student's major is finance.
= 1 if student's major is finance.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
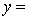
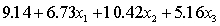 .
.  S = 15.0 R-Sq = 44.2%.
S = 15.0 R-Sq = 44.2%.  Do these results allow us to conclude at the 1% significance level that on average finance majors outperform those whose majors are not accounting or finance?
Do these results allow us to conclude at the 1% significance level that on average finance majors outperform those whose majors are not accounting or finance?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 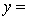
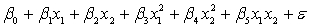 .
.
Where:
y = number of annual fatalities per shire.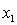 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 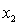 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS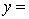
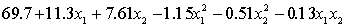 .
. 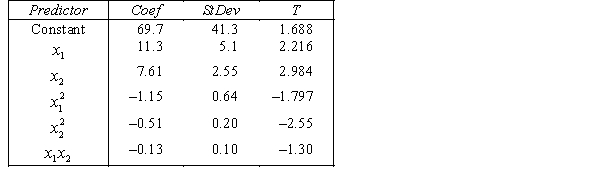 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Test at the 1% significance level to determine whether the interaction term should be retained in the model.
Test at the 1% significance level to determine whether the interaction term should be retained in the model.
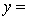
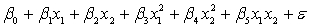 .
.Where:
y = number of annual fatalities per shire.
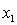 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 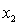 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
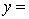
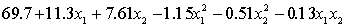 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 Test at the 1% significance level to determine whether the interaction term should be retained in the model.
Test at the 1% significance level to determine whether the interaction term should be retained in the model.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 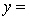
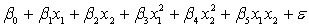 .
.
Where:
y = number of annual fatalities per shire.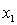 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 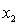 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS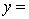
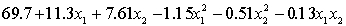 .
. 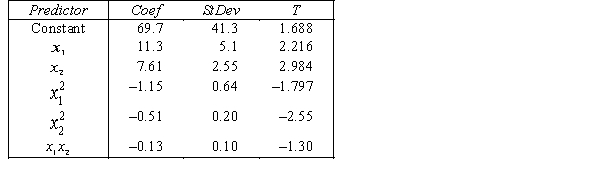 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE What is the multiple coefficient of determination? What does this statistic tell you about the model?
What is the multiple coefficient of determination? What does this statistic tell you about the model?
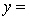
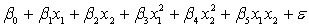 .
.Where:
y = number of annual fatalities per shire.
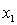 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 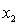 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
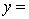
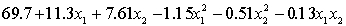 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 What is the multiple coefficient of determination? What does this statistic tell you about the model?
What is the multiple coefficient of determination? What does this statistic tell you about the model?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
An economist is in the process of developing a model to predict the price of gold. She believes that the two most important variables are the price of a barrel of oil 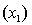 and the interest rate
and the interest rate 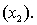 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 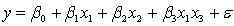 .
.
A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS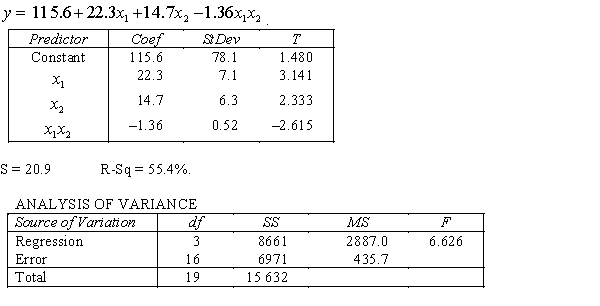 Is there sufficient evidence at the 1% significance level to conclude that the interest rate and the price of gold are linearly related?
Is there sufficient evidence at the 1% significance level to conclude that the interest rate and the price of gold are linearly related?
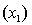 and the interest rate
and the interest rate 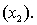 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 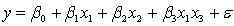 .
.A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS
 Is there sufficient evidence at the 1% significance level to conclude that the interest rate and the price of gold are linearly related?
Is there sufficient evidence at the 1% significance level to conclude that the interest rate and the price of gold are linearly related?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 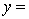
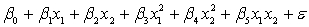 .
.
Where:
y = number of annual fatalities per shire.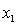 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 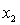 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS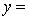
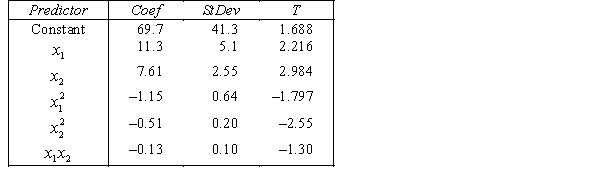
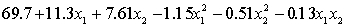 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE What does the coefficient of
What does the coefficient of 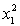 tell you about the model?
tell you about the model?
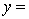
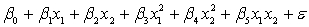 .
.Where:
y = number of annual fatalities per shire.
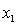 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 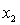 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
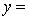
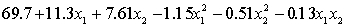 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 What does the coefficient of
What does the coefficient of 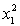 tell you about the model?
tell you about the model?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
An economist is analysing the incomes of professionals (physicians, dentists and lawyers). He realises that an important factor is the number of years of experience. However, he wants to know if there are differences among the three professional groups. He takes a random sample of 125 professionals and estimates the multiple regression model: 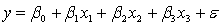 .
.
where
y
= annual income (in $1000).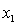 = years of experience.
= years of experience. 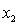 = 1 if physician.
= 1 if physician.
= 0 if not.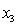 = 1 if dentist.
= 1 if dentist.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS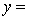
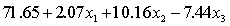 .
. 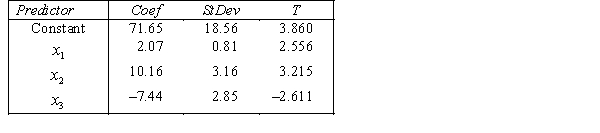 S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Is there enough evidence at the1% significant level to conclude that physicians earn more on average than lawyers?
Is there enough evidence at the1% significant level to conclude that physicians earn more on average than lawyers?
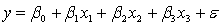 .
.where
y
= annual income (in $1000).
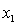 = years of experience.
= years of experience. 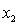 = 1 if physician.
= 1 if physician.= 0 if not.
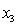 = 1 if dentist.
= 1 if dentist.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
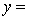
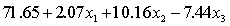 .
.  S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Is there enough evidence at the1% significant level to conclude that physicians earn more on average than lawyers?
Is there enough evidence at the1% significant level to conclude that physicians earn more on average than lawyers?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
An economist is in the process of developing a model to predict the price of gold. She believes that the two most important variables are the price of a barrel of oil 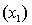 and the interest rate
and the interest rate 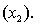 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 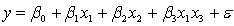 .
.
A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS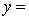
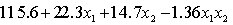 .
. 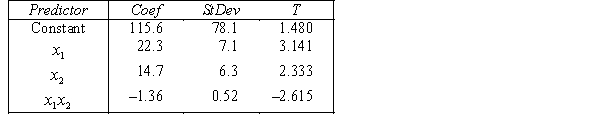 S = 20.9 R-Sq = 55.4%.
S = 20.9 R-Sq = 55.4%.  Interpret the coefficient
Interpret the coefficient 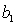 .
.
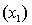 and the interest rate
and the interest rate 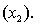 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 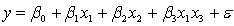 .
.A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS
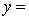
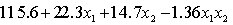 .
.  S = 20.9 R-Sq = 55.4%.
S = 20.9 R-Sq = 55.4%.  Interpret the coefficient
Interpret the coefficient 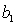 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
An economist is in the process of developing a model to predict the price of gold. She believes that the two most important variables are the price of a barrel of oil 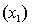 and the interest rate
and the interest rate 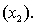 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 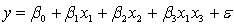 .
.
A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS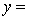
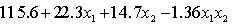 .
. 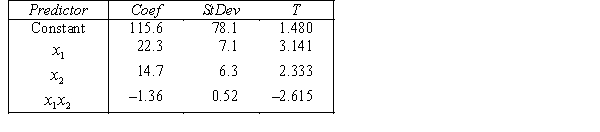 S = 20.9 R-Sq = 55.4%.
S = 20.9 R-Sq = 55.4%.  Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of gold?
Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of gold?
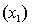 and the interest rate
and the interest rate 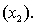 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 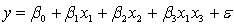 .
.A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS
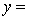
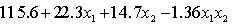 .
.  S = 20.9 R-Sq = 55.4%.
S = 20.9 R-Sq = 55.4%.  Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of gold?
Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of gold?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
An economist is in the process of developing a model to predict the price of gold. She believes that the two most important variables are the price of a barrel of oil 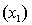 and the interest rate
and the interest rate 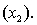 She proposes the first-order model with interaction:
She proposes the first-order model with interaction: 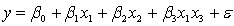 .
. 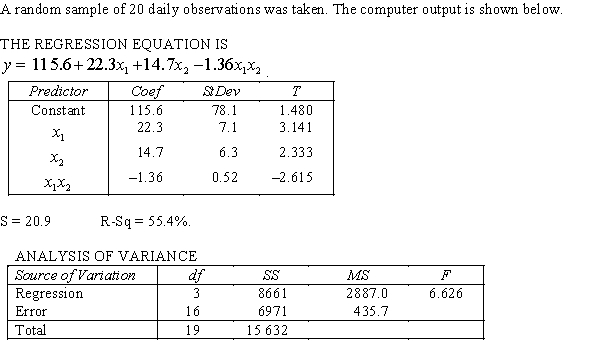 Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?
Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?
 and the interest rate
and the interest rate  She proposes the first-order model with interaction:
She proposes the first-order model with interaction:  .
.  Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?
Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
An economist is analysing the incomes of professionals (physicians, dentists and lawyers). He realises that an important factor is the number of years of experience. However, he wants to know if there are differences among the three professional groups. He takes a random sample of 125 professionals and estimates the multiple regression model: 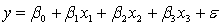 .
.
where
y
= annual income (in $1000).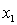 = years of experience.
= years of experience. 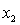 = 1 if physician.
= 1 if physician.
= 0 if not.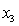 = 1 if dentist.
= 1 if dentist.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS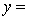
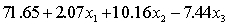 .
. 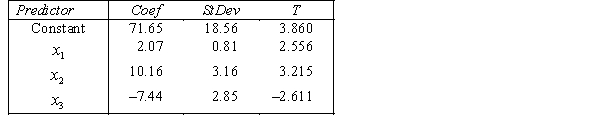 S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the income of professionals?
Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the income of professionals?
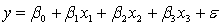 .
.where
y
= annual income (in $1000).
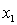 = years of experience.
= years of experience. 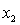 = 1 if physician.
= 1 if physician.= 0 if not.
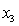 = 1 if dentist.
= 1 if dentist.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
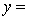
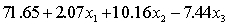 .
.  S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the income of professionals?
Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the income of professionals?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
A professor of accounting wanted to develop a multiple regression model to predict the students' grades in her fourth-year accounting course. She decides that the two most important factors are the student's grade point average (GPA) in the first three years and the student's major. She proposes the model: 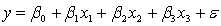 .
.
where
y
= fourth-year accounting course mark (out of 100).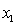 = GPA in first three years (range 0 to 12).
= GPA in first three years (range 0 to 12). 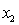 = 1 if student's major is accounting.
= 1 if student's major is accounting.
= 0 if not.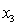 = 1 if student's major is finance.
= 1 if student's major is finance.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS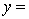
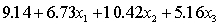 .
. 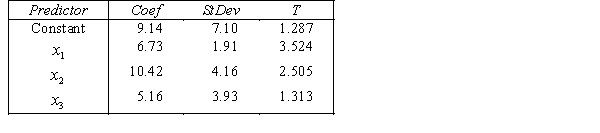 S = 15.0 R-Sq = 44.2%.
S = 15.0 R-Sq = 44.2%.  Do these results allow us to conclude at the 1% significance level that on average accounting majors outperform those whose majors are not accounting or finance?
Do these results allow us to conclude at the 1% significance level that on average accounting majors outperform those whose majors are not accounting or finance?
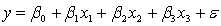 .
.where
y
= fourth-year accounting course mark (out of 100).
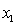 = GPA in first three years (range 0 to 12).
= GPA in first three years (range 0 to 12). 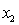 = 1 if student's major is accounting.
= 1 if student's major is accounting.= 0 if not.
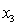 = 1 if student's major is finance.
= 1 if student's major is finance.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
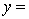
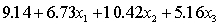 .
.  S = 15.0 R-Sq = 44.2%.
S = 15.0 R-Sq = 44.2%.  Do these results allow us to conclude at the 1% significance level that on average accounting majors outperform those whose majors are not accounting or finance?
Do these results allow us to conclude at the 1% significance level that on average accounting majors outperform those whose majors are not accounting or finance?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
An economist is analysing the incomes of professionals (physicians, dentists and lawyers). He realises that an important factor is the number of years of experience. However, he wants to know if there are differences among the three professional groups. He takes a random sample of 125 professionals and estimates the multiple regression model: 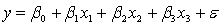 .
.
where
y
= annual income (in $1000).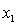 = years of experience.
= years of experience. 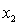 = 1 if physician.
= 1 if physician.
= 0 if not.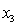 = 1 if dentist.
= 1 if dentist.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS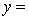
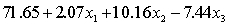 .
. 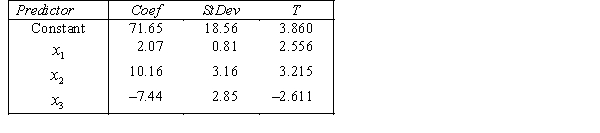 S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Is there enough evidence at the 10% significance level to conclude that dentists earn less on average than lawyers?
Is there enough evidence at the 10% significance level to conclude that dentists earn less on average than lawyers?
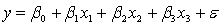 .
.where
y
= annual income (in $1000).
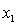 = years of experience.
= years of experience. 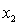 = 1 if physician.
= 1 if physician.= 0 if not.
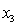 = 1 if dentist.
= 1 if dentist.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
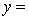
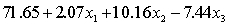 .
.  S = 42.6 R-Sq = 30.9%.
S = 42.6 R-Sq = 30.9%.  Is there enough evidence at the 10% significance level to conclude that dentists earn less on average than lawyers?
Is there enough evidence at the 10% significance level to conclude that dentists earn less on average than lawyers?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: 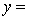
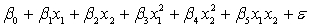 .
.
Where:
y = number of annual fatalities per shire.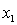 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 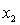 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS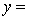
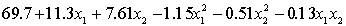 .
. 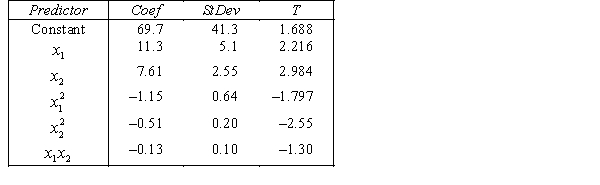 S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE What does the coefficient of
What does the coefficient of 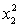 tell you about the model?
tell you about the model?
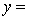
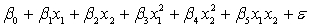 .
.Where:
y = number of annual fatalities per shire.
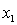 = number of cars registered in the shire (in units of 10 000).
= number of cars registered in the shire (in units of 10 000). 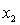 = number of trucks registered in the shire (in units of 1000).
= number of trucks registered in the shire (in units of 1000).The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS
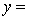
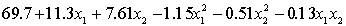 .
.  S = 15.2 R-Sq = 47.2%.
S = 15.2 R-Sq = 47.2%.ANALYSIS OF VARIANCE
 What does the coefficient of
What does the coefficient of 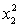 tell you about the model?
tell you about the model?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
A professor of accounting wanted to develop a multiple regression model to predict the students' grades in her fourth-year accounting course. She decides that the two most important factors are the student's grade point average (GPA) in the first three years and the student's major. She proposes the model: 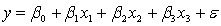 .
.
where
y
= fourth-year accounting course mark (out of 100).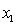 = GPA in first three years (range 0 to 12).
= GPA in first three years (range 0 to 12). 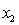 = 1 if student's major is accounting.
= 1 if student's major is accounting.
= 0 if not.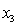 = 1 if student's major is finance.
= 1 if student's major is finance.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS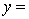
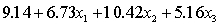 .
. 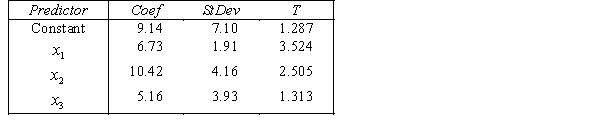 S = 15.0 R-Sq = 44.2%.
S = 15.0 R-Sq = 44.2%.  Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the fourth-year accounting course mark?
Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the fourth-year accounting course mark?
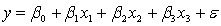 .
.where
y
= fourth-year accounting course mark (out of 100).
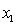 = GPA in first three years (range 0 to 12).
= GPA in first three years (range 0 to 12). 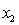 = 1 if student's major is accounting.
= 1 if student's major is accounting.= 0 if not.
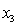 = 1 if student's major is finance.
= 1 if student's major is finance.= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS
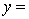
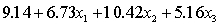 .
.  S = 15.0 R-Sq = 44.2%.
S = 15.0 R-Sq = 44.2%.  Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the fourth-year accounting course mark?
Do these results allow us to conclude at the 1% significance level that the model is useful in predicting the fourth-year accounting course mark?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


