Deck 6: Distribution and Network Problems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/54
Play
Full screen (f)
Deck 6: Distribution and Network Problems
1
Consider a maximal flow problem in which vehicle traffic entering a city is routed among several routes before eventually leaving the city. When represented with a network,
A)the nodes represent stoplights.
B)the arcs represent one way streets.
C)the nodes represent locations where speed limits change.
D)None of the alternatives is correct.
A)the nodes represent stoplights.
B)the arcs represent one way streets.
C)the nodes represent locations where speed limits change.
D)None of the alternatives is correct.
B
2
We assume in the maximal flow problem that
A)the flow out of a node is equal to the flow into the node.
B)the source and sink nodes are at opposite ends of the network.
C)the number of arcs entering a node is equal to the number of arcs exiting the node.
D)None of the alternatives is correct.
A)the flow out of a node is equal to the flow into the node.
B)the source and sink nodes are at opposite ends of the network.
C)the number of arcs entering a node is equal to the number of arcs exiting the node.
D)None of the alternatives is correct.
A
3
In the general linear programming model of the assignment problem,
A)one agent can do parts of several tasks.
B)one task can be done by several agents.
C)each agent is assigned to its own best task.
D)one agent is assigned to one and only one task.
A)one agent can do parts of several tasks.
B)one task can be done by several agents.
C)each agent is assigned to its own best task.
D)one agent is assigned to one and only one task.
D
4
Consider a shortest route problem in which a bank courier must travel between branches and the main operations center. When represented with a network,
A)the branches are the arcs and the operations center is the node.
B)the branches are the nodes and the operations center is the source.
C)the branches and the operations center are all nodes and the streets are the arcs.
D)the branches are the network and the operations center is the node.
A)the branches are the arcs and the operations center is the node.
B)the branches are the nodes and the operations center is the source.
C)the branches and the operations center are all nodes and the streets are the arcs.
D)the branches are the network and the operations center is the node.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
5
The assignment problem is a special case of the
A)transportation problem.
B)transshipment problem.
C)maximal flow problem.
D)shortest-route problem.
A)transportation problem.
B)transshipment problem.
C)maximal flow problem.
D)shortest-route problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
6
The shortest-route problem finds the shortest-route
A)from the source to the sink.
B)from the source to any other node.
C)from any node to any other node.
D)from any node to the sink.
A)from the source to the sink.
B)from the source to any other node.
C)from any node to any other node.
D)from any node to the sink.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following is not true regarding an LP model of the assignment problem?
A)Costs appear in the objective function only.
B)All constraints are of the form.
C)All constraint left-hand side coefficient values are 1.
D)All decision variable values are either 0 or 1.
A)Costs appear in the objective function only.
B)All constraints are of the form.
C)All constraint left-hand side coefficient values are 1.
D)All decision variable values are either 0 or 1.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
8
In a transshipment problem, shipments
A)cannot occur between two origin nodes.
B)cannot occur between an origin node and a destination node.
C)cannot occur between a transshipment node and a destination node.
D)can occur between any two nodes.
A)cannot occur between two origin nodes.
B)cannot occur between an origin node and a destination node.
C)cannot occur between a transshipment node and a destination node.
D)can occur between any two nodes.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
9
Constraints in a transshipment problem
A)correspond to arcs.
B)include a variable for every arc.
C)require the sum of the shipments out of an origin node to equal supply.
D)All of the alternatives are correct.
A)correspond to arcs.
B)include a variable for every arc.
C)require the sum of the shipments out of an origin node to equal supply.
D)All of the alternatives are correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
10
The assignment problem constraint x31 + x32 + x33 + x34 2 means
A)agent 3 can be assigned to 2 tasks.
B)agent 2 can be assigned to 3 tasks.
C)a mixture of agents 1, 2, 3, and 4 will be assigned to tasks.
D)there is no feasible solution.
A)agent 3 can be assigned to 2 tasks.
B)agent 2 can be assigned to 3 tasks.
C)a mixture of agents 1, 2, 3, and 4 will be assigned to tasks.
D)there is no feasible solution.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
11
Arcs in a transshipment problem
A)must connect every node to a transshipment node.
B)represent the cost of shipments.
C)indicate the direction of the flow.
D)All of the alternatives are correct.
A)must connect every node to a transshipment node.
B)represent the cost of shipments.
C)indicate the direction of the flow.
D)All of the alternatives are correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
12
The difference between the transportation and assignment problems is that
A)total supply must equal total demand in the transportation problem
B)the number of origins must equal the number of destinations in the transportation problem
C)each supply and demand value is 1 in the assignment problem
D)there are many differences between the transportation and assignment problems
A)total supply must equal total demand in the transportation problem
B)the number of origins must equal the number of destinations in the transportation problem
C)each supply and demand value is 1 in the assignment problem
D)there are many differences between the transportation and assignment problems

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
13
The parts of a network that represent the origins are
A)the capacities
B)the flows
C)the nodes
D)the arcs
A)the capacities
B)the flows
C)the nodes
D)the arcs

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
14
Converting a transportation problem LP from cost minimization to profit maximization requires only changing the objective function; the conversion does not affect the constraints.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
15
The number of units shipped from origin i to destination j is represented by
A)xij.
B)xji.
C)cij.
D)cji.
A)xij.
B)xji.
C)cij.
D)cji.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
16
The objective of the transportation problem is to
A)identify one origin that can satisfy total demand at the destinations and at the same time minimize total shipping cost.
B)minimize the number of origins used to satisfy total demand at the destinations.
C)minimize the number of shipments necessary to satisfy total demand at the destinations.
D)minimize the cost of shipping products from several origins to several destinations.
A)identify one origin that can satisfy total demand at the destinations and at the same time minimize total shipping cost.
B)minimize the number of origins used to satisfy total demand at the destinations.
C)minimize the number of shipments necessary to satisfy total demand at the destinations.
D)minimize the cost of shipping products from several origins to several destinations.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
17
Whenever total supply is less than total demand in a transportation problem, the LP model does not determine how the unsatisfied demand is handled.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is not true regarding the linear programming formulation of a transportation problem?
A)Costs appear only in the objective function.
B)The number of variables is (number of origins) * (number of destinations).
C)The number of constraints is (number of origins) * (number of destinations).
D)The constraints' left-hand side coefficients are either 0 or 1.
A)Costs appear only in the objective function.
B)The number of variables is (number of origins) * (number of destinations).
C)The number of constraints is (number of origins) * (number of destinations).
D)The constraints' left-hand side coefficients are either 0 or 1.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
19
The problem which deals with the distribution of goods from several sources to several destinations is the
A)maximal flow problem
B)transportation problem
C)assignment problem
D)shortest-route problem
A)maximal flow problem
B)transportation problem
C)assignment problem
D)shortest-route problem

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
20
A transportation problem with 3 sources and 4 destinations will have 7 decision variables.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
21
Explain how the general linear programming model of the assignment problem can be modified to handle problems involving a maximization function, unacceptable assignments, and supply not equally demand.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
22
Transshipment problem allows shipments both in and out of some nodes while transportation problems do not.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
23
The shortest-route problem is a special case of the transshipment problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
24
Explain what adjustments are made to the transportation linear program when there are unacceptable routes.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
25
Define the variables and constraints necessary in the LP formulation of the transshipment problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
26
The maximal flow problem can be formulated as a capacitated transshipment problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
27
A dummy origin in a transportation problem is used when supply exceeds demand.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
28
In the LP formulation of a maximal flow problem, a conservation-of-flow constraint ensures that an arc's flow capacity is not exceeded.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
29
Define the variables and constraints necessary in the LP formulation of the maximal flow problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
30
When a route in a transportation problem is unacceptable, the corresponding variable can be removed from the LP formulation.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
31
Write the LP formulation for this transportation problem. 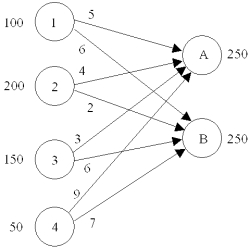


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
32
The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
33
How is the shortest-route problem like the transshipment problem?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
34
A transshipment constraint must contain a variable for every arc entering or leaving the node.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
35
Draw the network for this transportation problem. 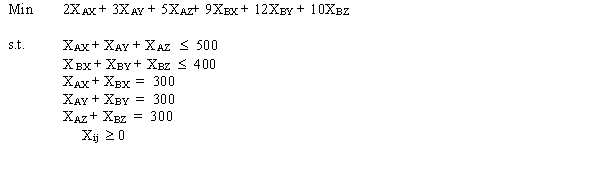

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
36
Is it a coincidence to obtain integer solutions to network problems? Explain.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
37
When the number of agents exceeds the number of tasks in an assignment problem, one or more dummy tasks must be introduced in the LP formulation or else the LP will not have a feasible solution.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
38
If a transportation problem has four origins and five destinations, the LP formulation of the problem will have nine constraints.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
39
How is the assignment linear program different from the transportation model?

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
40
The capacitated transportation problem includes constraints which reflect limited capacity on a route.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
41
The network below shows the flows possible between pairs of six locations. Formulate an LP to find the maximal flow possible from Node 1 to Node 6. 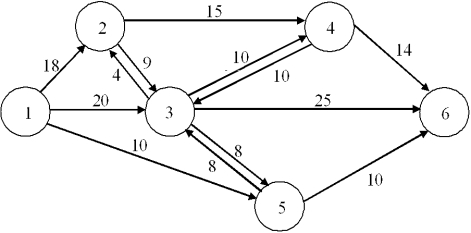


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the network below. Formulate the LP for finding the shortest-route path from node 1 to node 7. 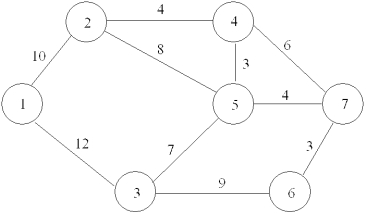


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
43
A network of railway lines connects the main lines entering and leaving a city. Speed limits, track reconstruction, and train length restrictions lead to the flow diagram below, where the numbers represent how many cars can pass per hour. Formulate an LP to find the maximal flow in cars per hour from Node 1 to Node F. 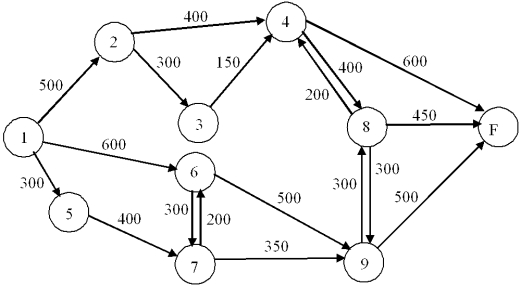


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
44
A beer distributor needs to plan how to make deliveries from its warehouse (Node 1) to a supermarket (Node 7), as shown in the network below. Develop the LP formulation for finding the shortest route from the warehouse to the supermarket. 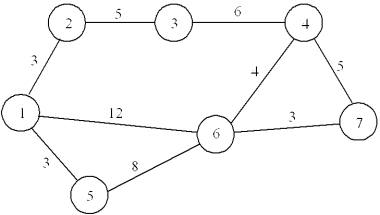


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
45
Canning Transport is to move goods from three factories to three distribution centers. Information about the move is given below. Give the network model and the linear programming model for this problem.  Shipping costs are:
Shipping costs are: 
 Shipping costs are:
Shipping costs are: 

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
46
The following table shows the unit shipping cost between cities, the supply at each source city, and the demand at each destination city. The Management Scientist solution is shown. Report the optimal solution. 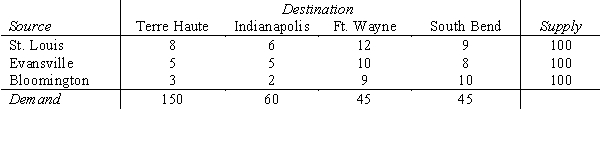 TRANSPORTATION PROBLEM
TRANSPORTATION PROBLEM
***************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
****************************** SUMMARY OF DESTINATION DEMANDS
SUMMARY OF DESTINATION DEMANDS
************************************* SUMMARY OF UNIT COST OR REVENUE DATA
SUMMARY OF UNIT COST OR REVENUE DATA
******************************************* OPTIMAL TRANSPORTATION SCHEDULE
OPTIMAL TRANSPORTATION SCHEDULE
************************************** TOTAL TRANSPORTATION COST OR REVENUE IS 1755
TOTAL TRANSPORTATION COST OR REVENUE IS 1755
 TRANSPORTATION PROBLEM
TRANSPORTATION PROBLEM***************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
******************************
 SUMMARY OF DESTINATION DEMANDS
SUMMARY OF DESTINATION DEMANDS*************************************
 SUMMARY OF UNIT COST OR REVENUE DATA
SUMMARY OF UNIT COST OR REVENUE DATA*******************************************
 OPTIMAL TRANSPORTATION SCHEDULE
OPTIMAL TRANSPORTATION SCHEDULE**************************************
 TOTAL TRANSPORTATION COST OR REVENUE IS 1755
TOTAL TRANSPORTATION COST OR REVENUE IS 1755
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
47
Peaches are to be transported from three orchard regions to two canneries. Intermediate stops at a consolidation station are possible.  Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem.
Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem. 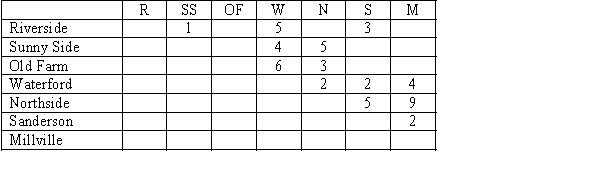
 Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem.
Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem. 

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
48
RVW (Restored Volkswagens) buys 15 used VW's at each of two car auctions each week held at different locations. It then transports the cars to repair shops it contracts with. When they are restored to RVW's specifications, RVW sells 10 each to three different used car lots. There are various costs associated with the average purchase and transportation prices from each auction to each repair shop. Also there are transportation costs from the repair shops to the used car lots. RVW is concerned with minimizing its total cost given the costs in the table below.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
49
Draw the network for this assignment problem.
Min
10x1A + 12x1B + 15x1C + 25x1D + 11x2A + 14x2B + 19x2C + 32x2D
+ 18x3A + 21x3B + 23x3C + 29x3D + 15x4A + 20x4B + 26x4C + 28x4D
s.t.
x1A + x1B + x1C + x1D = 1
x2A + x2B + x2C + x2D = 1
x3A + x3B + x3C + x3D = 1
x4A + x4B + x4C + x4D = 1
x1A + x2A + x3A + x4A = 1
x1B + x 2B + x3B + x4B = 1
x1C + x 2C + x3C + x4C = 1
x1D + x2D + x3D + x4D = 1
Min
10x1A + 12x1B + 15x1C + 25x1D + 11x2A + 14x2B + 19x2C + 32x2D
+ 18x3A + 21x3B + 23x3C + 29x3D + 15x4A + 20x4B + 26x4C + 28x4D
s.t.
x1A + x1B + x1C + x1D = 1
x2A + x2B + x2C + x2D = 1
x3A + x3B + x3C + x3D = 1
x4A + x4B + x4C + x4D = 1
x1A + x2A + x3A + x4A = 1
x1B + x 2B + x3B + x4B = 1
x1C + x 2C + x3C + x4C = 1
x1D + x2D + x3D + x4D = 1

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
50
Show both the network and the linear programming formulation for this assignment problem.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
51
A professor has been contacted by four not-for-profit agencies that are willing to work with student consulting teams. The agencies need help with such things as budgeting, information systems, coordinating volunteers, and forecasting. Although each of the four student teams could work with any of the agencies, the professor feels that there is a difference in the amount of time it would take each group to solve each problem. The professor's estimate of the time, in days, is given in the table below. Use the computer solution to see which team works with which project.  ASSIGNMENT PROBLEM
ASSIGNMENT PROBLEM
***********************
OBJECTIVE: MINIMIZATION
SUMMARY OF UNIT COST OR REVENUE DATA

 ASSIGNMENT PROBLEM
ASSIGNMENT PROBLEM***********************
OBJECTIVE: MINIMIZATION
SUMMARY OF UNIT COST OR REVENUE DATA



Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the following shortest-route problem involving seven cities. The distances between the cities are given below. Draw the network model for this problem and formulate the LP for finding the shortest route from City 1 to City 7.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
53
Write the linear program for this transshipment problem. 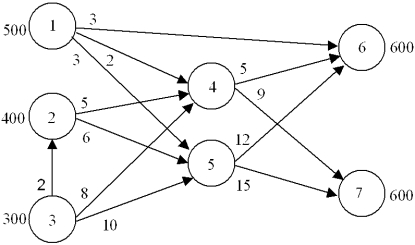


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the following shortest-route problem involving six cities with the distances given. Draw the network for this problem and formulate the LP for finding the shortest distance from City 1 to City 6. 


Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck


