Exam 6: Distribution and Network Problems
The maximal flow problem can be formulated as a capacitated transshipment problem.
True
Explain what adjustments are made to the transportation linear program when there are unacceptable routes.
When there are unacceptable routes in the transportation linear program, adjustments need to be made to ensure that the model reflects the reality of the situation. This may involve removing the unacceptable routes from the model and re-optimizing the transportation plan based on the remaining feasible routes. Alternatively, if the unacceptable routes are due to temporary issues such as road closures or maintenance, the model may need to be adjusted to account for these constraints and find alternative routes. In some cases, it may also be necessary to consider alternative modes of transportation or re-evaluate the supply and demand points to find a more feasible solution. Overall, the adjustments made to the transportation linear program when there are unacceptable routes aim to ensure that the model accurately represents the available transportation options and provides a realistic and efficient solution.
Write the linear program for this transshipment problem. 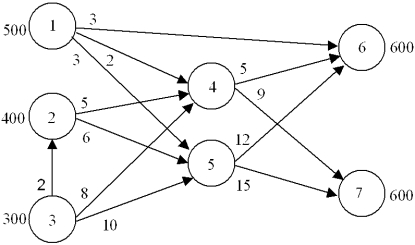
Min
3x16 + 2x14 + 3x15 + 5x24 + 6x25 + 2x32 + 8x 34 + 10x35 + 5x46 + 9x47 + 12x56
+ 15x57
s.t.x16 + x14 + x35 500
x24 + x25 - x23 400
x32 + x34 + x35 300
x46 + x47 - (x14 + x24 + x34) = 0
x56 + x57 - (x15 + x25 + x35) = 0
x16 + x46 + x56 = 600
x56 + x57 = 600
The difference between the transportation and assignment problems is that
Whenever total supply is less than total demand in a transportation problem, the LP model does not determine how the unsatisfied demand is handled.
Transshipment problem allows shipments both in and out of some nodes while transportation problems do not.
How is the assignment linear program different from the transportation model?
The shortest-route problem is a special case of the transshipment problem.
A professor has been contacted by four not-for-profit agencies that are willing to work with student consulting teams. The agencies need help with such things as budgeting, information systems, coordinating volunteers, and forecasting. Although each of the four student teams could work with any of the agencies, the professor feels that there is a difference in the amount of time it would take each group to solve each problem. The professor's estimate of the time, in days, is given in the table below. Use the computer solution to see which team works with which project. Projects Team Budgeting Information Volunteers Forecasting A 32 35 15 27 B 38 40 18 35 C 41 42 25 38 D 45 45 30 42 ASSIGNMENT PROBLEM
***********************
OBJECTIVE: MINIMIZATION
SUMMARY OF UNIT COST OR REVENUE DATA TASK AGENT 1 2 3 4 \@cdots \@cdots \@cdots \@cdots \@cdots 1 32 35 15 27 2 38 40 18 35 3 41 42 25 38 4 45 45 30 42 OPTIMAL ASSIGNMENTS COST/REVENUE ************ ********** ASSIGN AGENT 3 TO TASK 1 41 ASSIGN AGENT 4 TO TASK 2 45 ASSIGN AGENT 2 TO TASK 3 18 ASSIGN AGENT 1 TO TASK 4 27 TOTAL COST/REVENUE 131
A beer distributor needs to plan how to make deliveries from its warehouse (Node 1) to a supermarket (Node 7), as shown in the network below. Develop the LP formulation for finding the shortest route from the warehouse to the supermarket. 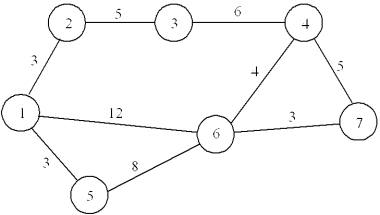
When a route in a transportation problem is unacceptable, the corresponding variable can be removed from the LP formulation.
Is it a coincidence to obtain integer solutions to network problems? Explain.
In the LP formulation of a maximal flow problem, a conservation-of-flow constraint ensures that an arc's flow capacity is not exceeded.
Consider a maximal flow problem in which vehicle traffic entering a city is routed among several routes before eventually leaving the city. When represented with a network,
The following table shows the unit shipping cost between cities, the supply at each source city, and the demand at each destination city. The Management Scientist solution is shown. Report the optimal solution. Destination Source Terre Haute Indianapolis Ft. Wayne South Bend Supply St. Louis 8 6 12 9 100 Evansville 5 5 10 8 100 Bloomington 3 2 9 10 100 Dem and 150 60 45 45 TRANSPORTATION PROBLEM
***************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
****************************** ORIGIN SUPPLY 1 100 2 100 3 100 SUMMARY OF DESTINATION DEMANDS
************************************* DESTINATION DEMAND 1 150 2 60 3 45 4 45 SUMMARY OF UNIT COST OR REVENUE DATA
******************************************* FROM TO DESTINATION ORIGIN 1 2 3 4 1 8 6 12 9 2 5 5 10 8 3 3 2 9 10 OPTIMAL TRANSPORTATION SCHEDULE
************************************** SHIP FROM TO DESTINATION ORIGIN 1 2 3 4 1 0 10 45 45 2 100 0 0 0 3 50 50 0 0 TOTAL TRANSPORTATION COST OR REVENUE IS 1755
The problem which deals with the distribution of goods from several sources to several destinations is the
Define the variables and constraints necessary in the LP formulation of the maximal flow problem.
Canning Transport is to move goods from three factories to three distribution centers. Information about the move is given below. Give the network model and the linear programming model for this problem. Source Supply Destination Demand A 200 50 B 100 125 C 150 125 Shipping costs are: Destination Source A 3 2 5 B 9 10 - C 5 6 4 (Source B cannot ship to destination Z)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)