Deck 9: Project Scheduling: Pertcpm
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/44
Play
Full screen (f)
Deck 9: Project Scheduling: Pertcpm
1
The earliest start time rule
A)compares the starting times of all activities for successors of an activity.
B)compares the finish times for all immediate predecessors of an activity.
C)determines when the project can begin.
D)determines when the project must begin.
A)compares the starting times of all activities for successors of an activity.
B)compares the finish times for all immediate predecessors of an activity.
C)determines when the project can begin.
D)determines when the project must begin.
B
2
Slack equals
A)LF - EF.
B)EF - LF.
C)EF - LS.
D)LF - ES.
A)LF - EF.
B)EF - LF.
C)EF - LS.
D)LF - ES.
EF - LF.
3
Activities K, M and S immediately follow activity H, and their latest start times are 14, 18, and 11. The latest finish time for activity H
A)is 11.
B)is 14.
C)is 18.
D)cannot be determined.
A)is 11.
B)is 14.
C)is 18.
D)cannot be determined.
A
4
Arcs in a project network indicate
A)completion times.
B)precedence relationships.
C)activities.
D)the critical path.
A)completion times.
B)precedence relationships.
C)activities.
D)the critical path.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
5
A path through a project network must reach every node.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
6
Which is not a significant challenge of project scheduling?
A)deadlines exist.
B)activities are independent.
C)many employees could be required.
D)delays are costly.
A)deadlines exist.
B)activities are independent.
C)many employees could be required.
D)delays are costly.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
7
The critical path
A)is any path that goes from the starting node to the completion node.
B)is a combination of all paths.
C)is the shortest path.
D)is the longest path.
A)is any path that goes from the starting node to the completion node.
B)is a combination of all paths.
C)is the shortest path.
D)is the longest path.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
8
PERT and CPM are applicable only when there is no dependence among activities.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
9
When activity times are uncertain,
A)assume they are normally distributed.
B)calculate the expected time, using (a + 4m + b)/6.
C)use the most likely time.
D)calculate the expected time, using (a + m + b)/3.
A)assume they are normally distributed.
B)calculate the expected time, using (a + 4m + b)/6.
C)use the most likely time.
D)calculate the expected time, using (a + m + b)/3.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
10
Activities with zero slack
A)can be delayed.
B)must be completed first.
C)lie on a critical path.
D)have no predecessors.
A)can be delayed.
B)must be completed first.
C)lie on a critical path.
D)have no predecessors.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
11
Critical activities are those that can be delayed without delaying the entire project.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
12
Activities following a node
A)can begin as soon as any activity preceding the node has been completed.
B)have an earliest start time equal to the largest of the earliest finish times for all activities entering the node.
C)have a latest start time equal to the largest of the earliest finish times for all activities entering the node.
D)None of the alternatives is correct.
A)can begin as soon as any activity preceding the node has been completed.
B)have an earliest start time equal to the largest of the earliest finish times for all activities entering the node.
C)have a latest start time equal to the largest of the earliest finish times for all activities entering the node.
D)None of the alternatives is correct.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
13
Activities G, P, and R are the immediate predecessors for activity W. If the earliest finish times for the three are 12, 15, and 10, then the earliest start time for W
A)is 10.
B)is 12.
C)is 15.
D)cannot be determined.
A)is 10.
B)is 12.
C)is 15.
D)cannot be determined.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
14
To determine how to crash activity times
A)normal activity costs and costs under maximum crashing must be known.
B)shortest times with crashing must be known.
C)realize that new paths may become critical.
D)All of the alternatives are true.
A)normal activity costs and costs under maximum crashing must be known.
B)shortest times with crashing must be known.
C)realize that new paths may become critical.
D)All of the alternatives are true.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
15
For an activity with more than one immediate successor activity, its latest-finish time is equal to the
A)largest latest-finish time among its immediate successors.
B)smallest latest-finish time among its immediate successors.
C)largest latest-start time among its immediate successors.
D)smallest latest-start time among its immediate successors.
A)largest latest-finish time among its immediate successors.
B)smallest latest-finish time among its immediate successors.
C)largest latest-start time among its immediate successors.
D)smallest latest-start time among its immediate successors.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
16
For an activity with more than one immediate predecessor activity, which of the following is used to compute its earliest finish (EF) time?
A)the largest EF among the immediate predecessors.
B)the average EF among the immediate predecessors.
C)the largest LF among the immediate predecessors.
D)the difference in EF among the immediate predecessors.
A)the largest EF among the immediate predecessors.
B)the average EF among the immediate predecessors.
C)the largest LF among the immediate predecessors.
D)the difference in EF among the immediate predecessors.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
17
In deciding which activities to crash, one must
A)crash all critical activities.
B)crash largest-duration activities.
C)crash lowest-cost activities.
D)crash activities on the critical path(s) only.
A)crash all critical activities.
B)crash largest-duration activities.
C)crash lowest-cost activities.
D)crash activities on the critical path(s) only.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is always true about a critical activity?
A)LS = EF.
B)LF = LS.
C)ES = LS.
D)EF = ES.
A)LS = EF.
B)LF = LS.
C)ES = LS.
D)EF = ES.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
19
PERT and CPM
A)are most valuable when a small number of activities must be scheduled.
B)have different features and are not applied to the same situation.
C)do not require a chronological relationship among activities.
D)have been combined to develop a procedure that uses the best of each.
A)are most valuable when a small number of activities must be scheduled.
B)have different features and are not applied to the same situation.
C)do not require a chronological relationship among activities.
D)have been combined to develop a procedure that uses the best of each.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following is a general rule for crashing activities?
A)Crash only non-critical activities.
B)Crash activities with zero slack.
C)Crash activities with the greatest number of predecessors.
D)Crash the path with the fewest activities.
A)Crash only non-critical activities.
B)Crash activities with zero slack.
C)Crash activities with the greatest number of predecessors.
D)Crash the path with the fewest activities.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
21
Crashing refers to an unanticipated delay in a critical path activity that causes the total time to exceed its limit.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
22
The project manager should monitor the progress of any activity with a large time variance even if the expected time does not identify the activity as a critical activity.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
23
Name at least three managerial situations where answers are provided by project management solutions.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
24
Why should projects be monitored after the critical path is found?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
25
The length of time an activity can be delayed without affecting the project completion time is the slack.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
26
Once the earliest and latest times are calculated, how is the critical path determined?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
27
The latest finish time for an activity is the largest of the latest start times for all activities that immediately follow the activity.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
28
Explain how and why all predecessor activities must be considered when finding the earliest start time.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
29
A critical activity can be part of a noncritical path.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
30
A project network is shown below. Use a forward and a backward pass to determine the critical path, and then fill out the table below. 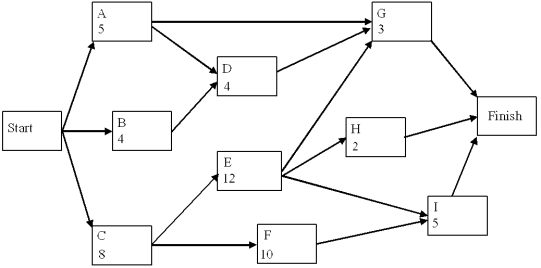
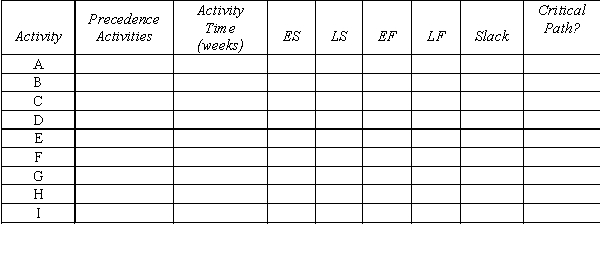 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?

 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
31
The earliest finish time for the final activity is the project duration.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
32
Constraints in the LP models for crashing decisions are required to compare the activity's earliest finish time with the earliest finish time of each predecessor.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
33
When activity times are uncertain, total project time is normally distributed with mean equal to the sum of the means of all of the critical activities.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
34
The variance in the project completion time is the sum of the variances of all activities in the project.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
35
When activity times are uncertain, an activity's most likely time is the same as its expected time.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
36
A project network is shown below. Use a forward and a backward pass to determine the critical path, and then fill out the table below. 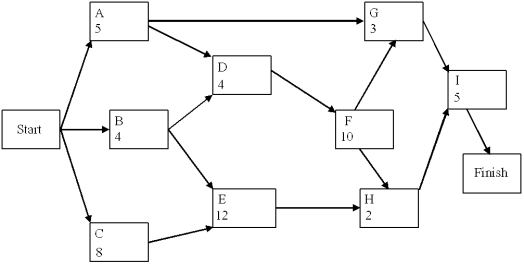
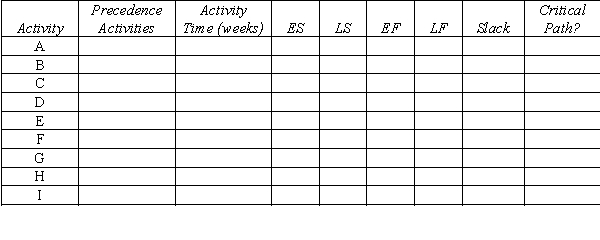 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?

 Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?
Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in fewer than 25 weeks more or less than 50%?
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
37
The earliest start time for an activity is equal to the smallest of the earliest finish times for all its immediate predecessors.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
38
The linear programming model for crashing presented in the textbook assumes that any portion of the activity crash time can be achieved for a corresponding portion of the activity crashing cost.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
39
From this schedule of activities, draw the PERT/CPM network. 


Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
40
Explain how and why all successor activities must be considered when finding the latest finish time.

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
41
Given the following network with activities and times estimated in days, 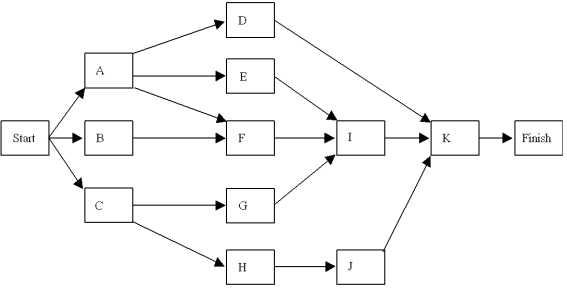
a.What are the critical path activities?
b.What is the expected time to complete the project?
c.What is the probability the project will take more than 28 days to complete?

a.What are the critical path activities?
b.What is the expected time to complete the project?
c.What is the probability the project will take more than 28 days to complete?

Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
42
Use the following network of related activities with their duration times to complete a row for each activity under the column headings below. 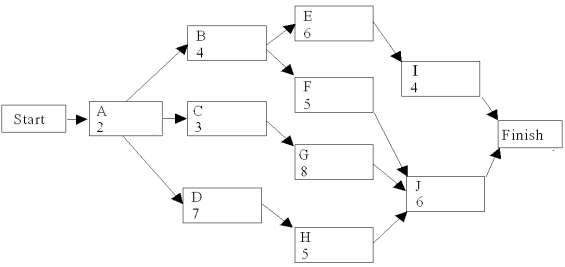



Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
43
Use the following network of related activities with their duration times to complete a row for each activity under the column headings below. 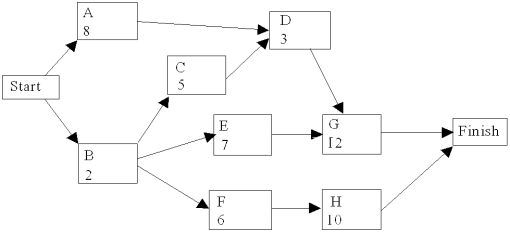



Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck
44
The critical path for this network is A - E - F and the project completion time is 22 weeks. 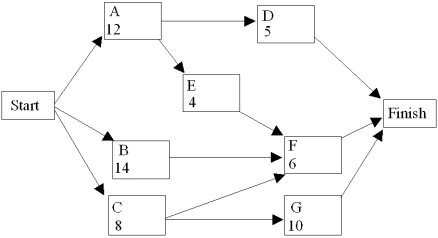 If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision.
If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision.
 If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision.
If a deadline of 17 weeks is imposed, give the linear programming model for the crashing decision. 
Unlock Deck
Unlock for access to all 44 flashcards in this deck.
Unlock Deck
k this deck


