Exam 9: Project Scheduling: Pertcpm
Exam 1: Introduction49 Questions
Exam 2: An Introduction to Linear Programming52 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution47 Questions
Exam 4: Linear Programming Applications in Marketing, Finance and Operations Management38 Questions
Exam 5: Advanced Linear Programming Applications35 Questions
Exam 6: Distribution and Network Problems54 Questions
Exam 7: Integer Linear Programming43 Questions
Exam 8: Nonlinear Optimization Models48 Questions
Exam 9: Project Scheduling: Pertcpm44 Questions
Exam 10: Inventory Models51 Questions
Exam 11: Waiting Line Models48 Questions
Exam 12: Simulation49 Questions
Exam 13: Decision Analysis42 Questions
Exam 14: Multicriteria Decisions45 Questions
Exam 15: Forecasting47 Questions
Exam 16: Markov Processes41 Questions
Exam 17: Linear Programming: Simplex Method46 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality34 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems42 Questions
Exam 20: Minimal Spanning Tree18 Questions
Exam 21: Dynamic Programming30 Questions
Select questions type
The latest finish time for an activity is the largest of the latest start times for all activities that immediately follow the activity.
Free
(True/False)
4.8/5  (39)
(39)
Correct Answer:
False
Which is not a significant challenge of project scheduling?
Free
(Multiple Choice)
4.7/5  (39)
(39)
Correct Answer:
B
The variance in the project completion time is the sum of the variances of all activities in the project.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
False
Which of the following is always true about a critical activity?
(Multiple Choice)
4.8/5  (40)
(40)
Which of the following is a general rule for crashing activities?
(Multiple Choice)
4.8/5  (37)
(37)
The length of time an activity can be delayed without affecting the project completion time is the slack.
(True/False)
4.8/5  (29)
(29)
Explain how and why all successor activities must be considered when finding the latest finish time.
(Essay)
4.9/5  (39)
(39)
Use the following network of related activities with their duration times to complete a row for each activity under the column headings below. 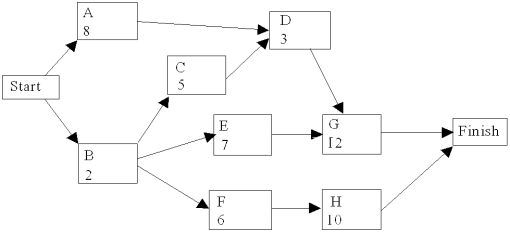 Activity Immediate Predecessors Activity Time ES LS EF LF Sack Critical Path?
Activity Immediate Predecessors Activity Time ES LS EF LF Sack Critical Path?
(Essay)
4.9/5  (28)
(28)
When activity times are uncertain, an activity's most likely time is the same as its expected time.
(True/False)
4.8/5  (33)
(33)
The earliest finish time for the final activity is the project duration.
(True/False)
4.8/5  (39)
(39)
A project network is shown below. Use a forward and a backward pass to determine the critical path, and then fill out the table below. 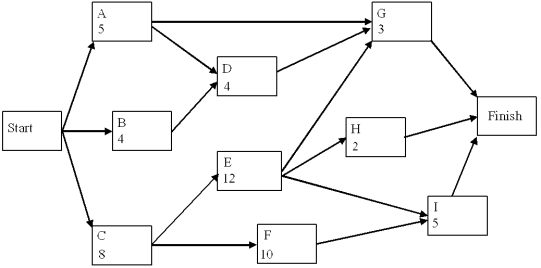 Activity Precedence Activities Activity Time (weeks) ES LS EF LF Slack Critical Path? Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
Activity Precedence Activities Activity Time (weeks) ES LS EF LF Slack Critical Path? Now assume that the times listed are only the expected times instead of being fixed times. Is the probability of being finished in more than 28 weeks more or less than 50%?
(Essay)
4.8/5  (30)
(30)
For an activity with more than one immediate successor activity, its latest-finish time is equal to the
(Multiple Choice)
4.9/5  (40)
(40)
The project manager should monitor the progress of any activity with a large time variance even if the expected time does not identify the activity as a critical activity.
(True/False)
4.9/5  (42)
(42)
Name at least three managerial situations where answers are provided by project management solutions.
(Essay)
4.8/5  (32)
(32)
Constraints in the LP models for crashing decisions are required to compare the activity's earliest finish time with the earliest finish time of each predecessor.
(True/False)
4.8/5  (43)
(43)
Activities K, M and S immediately follow activity H, and their latest start times are 14, 18, and 11. The latest finish time for activity H
(Multiple Choice)
4.8/5  (36)
(36)
Use the following network of related activities with their duration times to complete a row for each activity under the column headings below. 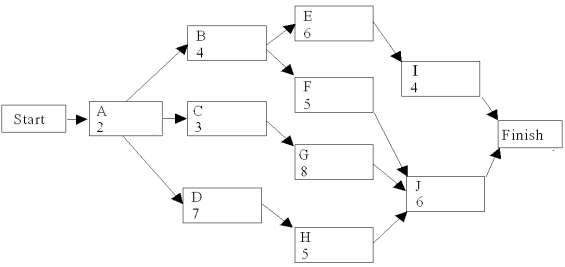 Activity Immediate Predecessors Time (weeks) ES LS EF LF Sack Critical Path? A B
Activity Immediate Predecessors Time (weeks) ES LS EF LF Sack Critical Path? A B
(Essay)
4.8/5  (35)
(35)
Showing 1 - 20 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)