Deck 17: Linear Programming: Simplex Method
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/46
Play
Full screen (f)
Deck 17: Linear Programming: Simplex Method
1
In the simplex method, a tableau is optimal only if all the cj -zj values are
A)zero or negative.
B)zero.
C)negative and nonzero.
D)positive and nonzero.
A)zero or negative.
B)zero.
C)negative and nonzero.
D)positive and nonzero.
zero or negative.
2
When there is a tie between two or more variables for removal from the simplex tableau,
A)post-optimality analysis is required.
B)their dual prices will be equal.
C)converting the pivot element will break the tie.
D)a condition of degeneracy is present.
A)post-optimality analysis is required.
B)their dual prices will be equal.
C)converting the pivot element will break the tie.
D)a condition of degeneracy is present.
D
3
The values in the cj - zj , or net evaluation, row indicate
A)the value of the objective function.
B)the decrease in value of the objective function that will result if one unit of the variable corresponding to the jth column of the A matrix is brought into the basis.
C)the net change in the value of the objective function that will result if one unit of the variable corresponding to the jth column of the A matrix is brought into the basis.
D)the values of the decision variables.
A)the value of the objective function.
B)the decrease in value of the objective function that will result if one unit of the variable corresponding to the jth column of the A matrix is brought into the basis.
C)the net change in the value of the objective function that will result if one unit of the variable corresponding to the jth column of the A matrix is brought into the basis.
D)the values of the decision variables.
the net change in the value of the objective function that will result if one unit of the variable corresponding to the jth column of the A matrix is brought into the basis.
4
Every extreme point of the graph of a two variable linear programming problem is a basic feasible solution.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
5
Infeasibility exists when one or more of the artificial variables
A)remain in the final solution as a negative value.
B)remain in the final solution as a positive value.
C)have been removed from the basis.
D)remain in the basis.
A)remain in the final solution as a negative value.
B)remain in the final solution as a positive value.
C)have been removed from the basis.
D)remain in the basis.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
6
An alternative optimal solution is indicated when in the simplex tableau
A)a non-basic variable has a value of zero in the cj -zj row.
B)a basic variable has a positive value in the cj -zj row.
C)a basic variable has a value of zero in the cj - zj row.
D)a non-basic variable has a positive value in the cj - zj row.
A)a non-basic variable has a value of zero in the cj -zj row.
B)a basic variable has a positive value in the cj -zj row.
C)a basic variable has a value of zero in the cj - zj row.
D)a non-basic variable has a positive value in the cj - zj row.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
7
Unit columns are used to identify
A)the tableau.
B)the c row.
C)the b column.
D)the basic variables.
A)the tableau.
B)the c row.
C)the b column.
D)the basic variables.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
8
What coefficient is assigned to an artificial variable in the objective function?
A)zero.
B)one.
C)a very large negative number.
D)a very large positive number.
A)zero.
B)one.
C)a very large negative number.
D)a very large positive number.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
9
Algebraic methods such as the simplex method are used to solve
A)nonlinear programming problems.
B)any size linear programming problem.
C)programming problems under uncertainty.
D)graphical models.
A)nonlinear programming problems.
B)any size linear programming problem.
C)programming problems under uncertainty.
D)graphical models.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following is not a step that is necessary to prepare a linear programming problem for solution using the simplex method?
A)formulate the problem.
B)set up the standard form by adding slack and/or subtracting surplus variables.
C)perform elementary row and column operations.
D)set up the tableau form.
A)formulate the problem.
B)set up the standard form by adding slack and/or subtracting surplus variables.
C)perform elementary row and column operations.
D)set up the tableau form.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
11
Which is not required for a problem to be in tableau form?
A)Each constraint must be written as an equation.
B)Each of the original decision variables must have a coefficient of 1 in one equation and 0 in every other equation.
C)There is exactly one basic variable in each constraint.
D)The right-hand side of each constraint must be nonnegative.
A)Each constraint must be written as an equation.
B)Each of the original decision variables must have a coefficient of 1 in one equation and 0 in every other equation.
C)There is exactly one basic variable in each constraint.
D)The right-hand side of each constraint must be nonnegative.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
12
A basic solution and a basic feasible solution
A)are the same thing.
B)differ in the number of variables allowed to be zero.
C)describe interior points and exterior points, respectively.
D)differ in their inclusion of nonnegativity restrictions.
A)are the same thing.
B)differ in the number of variables allowed to be zero.
C)describe interior points and exterior points, respectively.
D)differ in their inclusion of nonnegativity restrictions.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
13
When a set of simultaneous equations has more variables than constraints,
A)it is a basic set.
B)it is a feasible set.
C)there is a unique solution.
D)there are many solutions.
A)it is a basic set.
B)it is a feasible set.
C)there is a unique solution.
D)there are many solutions.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
14
The basic solution to a problem with three equations and four variables would assign a value of 0 to
A)0 variables.
B)1 variable.
C)3 variables.
D)7 variables.
A)0 variables.
B)1 variable.
C)3 variables.
D)7 variables.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
15
When a system of simultaneous equations has more variables than equations, there is a unique solution.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
16
A minimization problem with four decision variables, two greater-than-or-equal-to constraints, and one equality constraint will have
A)2 surplus variables, 3 artificial variables, and 3 variables in the basis.
B)4 surplus variables, 2 artificial variables, and 4 variables in the basis.
C)3 surplus variables, 3 artificial variables, and 4 variables in the basis.
D)2 surplus variables, 2 artificial variables, and 3 variables in the basis.
A)2 surplus variables, 3 artificial variables, and 3 variables in the basis.
B)4 surplus variables, 2 artificial variables, and 4 variables in the basis.
C)3 surplus variables, 3 artificial variables, and 4 variables in the basis.
D)2 surplus variables, 2 artificial variables, and 3 variables in the basis.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
17
To determine a basic solution set of n-m, the variables equal to zero and solve the m linear constraint equations for the remaining m variables.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
18
In a simplex tableau, there is a variable associated with each column and both a constraint and a basic variable associated with each row.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
19
The purpose of the tableau form is to provide
A)infeasible solution.
B)optimal infeasible solution.
C)initial basic feasible solution.
D)degenerate solution.
A)infeasible solution.
B)optimal infeasible solution.
C)initial basic feasible solution.
D)degenerate solution.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
20
A basic feasible solution satisfies the nonnegativity restriction.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the following problem by the simplex method.
Max
100x1 + 120x2 + 85x3
s.t.
3x1 + 1x2 + 6x3 120
5x1 + 8x2 + 2x3 160
x1 , x2 , x3 0
Max
100x1 + 120x2 + 85x3
s.t.
3x1 + 1x2 + 6x3 120
5x1 + 8x2 + 2x3 160
x1 , x2 , x3 0

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
22
A solution is optimal when all values in the cj -zj row of the simplex tableau are either zero or positive.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
23
The variable to remove from the current basis is the variable with the smallest positive cj - zj value.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
24
Artificial variables are added for the purpose of obtaining an initial basic feasible solution.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
25
Coefficients in a nonbasic column in a simplex tableau indicate the amount of decrease in the current basic variables when the value of the nonbasic variable is increased from 0 to 1.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
26
We recognize infeasibility when one or more of the artificial variables do not remain in the solution at a positive value.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
27
What is an artificial variable? Why is it necessary?

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
28
If a variable is not in the basis, its value is 0.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
29
For the special cases of infeasibility, unboundedness, and alternate optimal solutions, tell what you would do next with your linear programming model if the case occurred.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
30
What is the criterion for entering a new variable into the basis?

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
31
A portion of a simplex tableau is  Give a complete explanation of the meaning of the z1 = 5 value as it relates to x2 and s2.
Give a complete explanation of the meaning of the z1 = 5 value as it relates to x2 and s2.
 Give a complete explanation of the meaning of the z1 = 5 value as it relates to x2 and s2.
Give a complete explanation of the meaning of the z1 = 5 value as it relates to x2 and s2.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the following problem by the simplex method.
Max
14x1 + 14.5x2 + 18x3
s.t.
x1 + 2x2 + 2.5x3 50
x1 + x2 + 1.5x3 30
x1 , x2 , x3 0
Max
14x1 + 14.5x2 + 18x3
s.t.
x1 + 2x2 + 2.5x3 50
x1 + x2 + 1.5x3 30
x1 , x2 , x3 0

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
33
A simplex table is shown below.
a.What is the current complete solution?
b.The 32/5 for z1 is composed of 0 + 8(4/5) + 0.Explain the meaning of this number.
c.Explain the meaning of the -12/5 value for c 2 - z2.
a.What is the current complete solution?
b.The 32/5 for z1 is composed of 0 + 8(4/5) + 0.Explain the meaning of this number.
c.Explain the meaning of the -12/5 value for c 2 - z2.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
34
The coefficient of an artificial variable in the objective function is zero.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
35
The purpose of row operations is to create a unit column for the entering variable while maintaining unit columns for the remaining basic variables.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
36
At each iteration of the simplex procedure, a new variable becomes basic and a currently basic variable becomes nonbasic, preserving the same number of basic variables and improving the value of the objective function.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
37
The variable to enter into the basis is the variable with the largest positive cj - zj value.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
38
A simplex tableau is shown below. 
a.Do one more iteration of the simplex procedure.
b.What is the current complete solution?
c.Is this solution optimal? Why or why not?

a.Do one more iteration of the simplex procedure.
b.What is the current complete solution?
c.Is this solution optimal? Why or why not?

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
39
Write the following problem in tableau form. Which variables would be in the initial basic solution?
Min Z
= 3x1 + 8x2
s.t.
x1 + x2 200
x1 80
x2 60
Min Z
= 3x1 + 8x2
s.t.
x1 + x2 200
x1 80
x2 60

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
40
Describe and illustrate graphically the special cases that can occur in a linear programming solution. What clues for these cases does the simplex procedure supply?

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
41
Write the following problem in tableau form. Which variables would be in the initial basis?
Max
x1 + 2x2
s.t.
3x1 + 4x2 100
2x1 + 3.5x2 60
2x1 -1x2 = 4
x1 , x2 0
Max
x1 + 2x2
s.t.
3x1 + 4x2 100
2x1 + 3.5x2 60
2x1 -1x2 = 4
x1 , x2 0

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
42
Comment on the solution shown in this simplex tableau. 


Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
43
Comment on the solution shown in this simplex tableau. 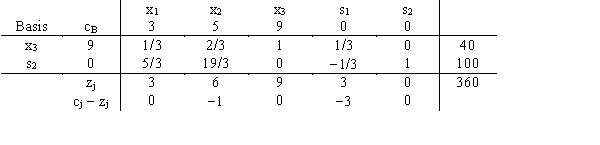


Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
44
Determine from a review of the following tableau whether the linear programming problem has multiple optimal solutions.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
45
Write the following problem in tableau form. Which variables would be in the initial basic solution?
Min Z
= -3x1 + x2 + x3
s.t.
x1 - 2x2 + x3 11
-4 x1 + x2 + 2x3 3
2x1 -x3 -1
Min Z
= -3x1 + x2 + x3
s.t.
x1 - 2x2 + x3 11
-4 x1 + x2 + 2x3 3
2x1 -x3 -1

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
46
Comment on the solution shown in this simplex tableau. 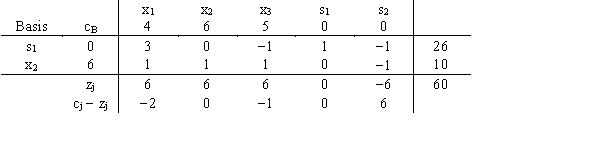


Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck


