Deck 16: Regression Analysis: Model Building
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/41
Play
Full screen (f)
Deck 16: Regression Analysis: Model Building
1
A model in the form of y = β0 + β1z1 + β2z2 + . . . + βpzp + ε, where each independent variable zj (for j = 1, 2, . . ., p) is a function of x1, x2,..., xk, is known as the _____ model.
A) general linear
B) general curvilinear
C) pth-order z
D) experimental
A) general linear
B) general curvilinear
C) pth-order z
D) experimental
general linear
2
The following model
Y = β0 + β1x1 + ε
Is referred to as a
A) curvilinear model.
B) curvilinear model with one predictor variable.
C) simple second-order model with one predictor variable.
D) simple first-order model with one predictor variable.
Y = β0 + β1x1 + ε
Is referred to as a
A) curvilinear model.
B) curvilinear model with one predictor variable.
C) simple second-order model with one predictor variable.
D) simple first-order model with one predictor variable.
simple first-order model with one predictor variable.
3
Models in which the parameters have exponents other than 1 are called
A) independent models.
B) nonlinear models.
C) autocorrelated models.
D) linear models.
A) independent models.
B) nonlinear models.
C) autocorrelated models.
D) linear models.
nonlinear models.
4
In multiple regression analysis, the general linear model
A) cannot be used to accommodate curvilinear relationships between dependent variables and independent variables.
B) can be used to accommodate curvilinear relationships between the independent variables and dependent variable.
C) must contain more than two independent variables.
D) cannot use the standard multiple regression procedures for estimation and prediction.
A) cannot be used to accommodate curvilinear relationships between dependent variables and independent variables.
B) can be used to accommodate curvilinear relationships between the independent variables and dependent variable.
C) must contain more than two independent variables.
D) cannot use the standard multiple regression procedures for estimation and prediction.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
5
When dealing with the problem of nonconstant variance, the reciprocal transformation means using
A) 1/x as the independent variable instead of x.
B) x2 as the independent variable instead of x.
C) y2 as the dependent variable instead of y.
D) 1/y as the dependent variable instead of y.
A) 1/x as the independent variable instead of x.
B) x2 as the independent variable instead of x.
C) y2 as the dependent variable instead of y.
D) 1/y as the dependent variable instead of y.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
6
All the independent variables in a multiple regression analysis
A) must be quantitative.
B) must be either quantitative or qualitative but not a mix of both.
C) must assume only positive values.
D) can be either quantitative or qualitative or both.
A) must be quantitative.
B) must be either quantitative or qualitative but not a mix of both.
C) must assume only positive values.
D) can be either quantitative or qualitative or both.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
7
A test used to determine whether or not first-order autocorrelation is present is _____ test.
A) serial-autocorrelation
B) t
C) chi-square
D) Durbin-Watson
A) serial-autocorrelation
B) t
C) chi-square
D) Durbin-Watson

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
8
A variable such as z, whose value is z = x1x2, is added to a general linear model in order to account for potential effects of two variables x1 and x2 acting together. This type of effect is
A) impossible to occur.
B) called interaction.
C) called multicollinearity effect.
D) one of the transformation effects.
A) impossible to occur.
B) called interaction.
C) called multicollinearity effect.
D) one of the transformation effects.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
9
The following regression model
Y = β0 + β1x1 + β2
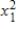
+ ε
is known as a
A) simple first-order model with one predictor variable.
B) second-order model with two predictor variables.
C) second-order model with one predictor variable.
D) simple first-order model with two predictor variables.
Y = β0 + β1x1 + β2
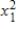
+ ε
is known as a
A) simple first-order model with one predictor variable.
B) second-order model with two predictor variables.
C) second-order model with one predictor variable.
D) simple first-order model with two predictor variables.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
10
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 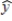 = 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
= 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
If you want to determine whether or not the coefficients of the independent variables are significant, the critical t value at α = .01 is
A) 2.080.
B) 2.831.
C) 2.518.
D) 2.807.
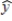 = 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
= 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
If you want to determine whether or not the coefficients of the independent variables are significant, the critical t value at α = .01 is
A) 2.080.
B) 2.831.
C) 2.518.
D) 2.807.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
11
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 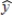 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
At the .01 level of significance, the coefficient of x3
A) is significant.
B) is not found to be significant.
C) cannot be tested, because not enough information is provided.
D) should be estimated again, because it is incorrect in the above equation.
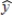 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
At the .01 level of significance, the coefficient of x3
A) is significant.
B) is not found to be significant.
C) cannot be tested, because not enough information is provided.
D) should be estimated again, because it is incorrect in the above equation.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
12
What value of Durbin-Watson statistic indicates no autocorrelation is present?
A) 1
B) 2
C) 4
D) 0
A) 1
B) 2
C) 4
D) 0

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
13
The joint effect of two independent variables acting together is called
A) autocorrelation.
B) interaction.
C) transformation.
D) joint regression.
A) autocorrelation.
B) interaction.
C) transformation.
D) joint regression.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
14
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 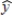 = 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
= 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
At the 5% level, the coefficient of x1
A) is significant.
B) is not found to be significant.
C) cannot be tested, because not enough information is provided.
D) should be estimated again, because it is incorrect in the above equation.
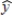 = 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
= 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
At the 5% level, the coefficient of x1
A) is significant.
B) is not found to be significant.
C) cannot be tested, because not enough information is provided.
D) should be estimated again, because it is incorrect in the above equation.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
15
Serial correlation is
A) the correlation between serial numbers of the independent variables.
B) the same as autocorrelation.
C) the same as leverage.
D) used to identify the effects of multicollinearity.
A) the correlation between serial numbers of the independent variables.
B) the same as autocorrelation.
C) the same as leverage.
D) used to identify the effects of multicollinearity.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
16
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 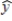 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3= 7
SST = 4900
SSE = 1296
At the 1% level, the coefficient of x2
A) is significant.
B) is not found to be significant.
C) cannot be tested, because not enough information is provided.
D) should be estimated again, because it is incorrect in the above equation.
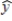 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3= 7
SST = 4900
SSE = 1296
At the 1% level, the coefficient of x2
A) is significant.
B) is not found to be significant.
C) cannot be tested, because not enough information is provided.
D) should be estimated again, because it is incorrect in the above equation.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
17
The correlation in error terms that arises when the error terms at successive points in time are related is termed
A) leverage.
B) multicorrelation.
C) autocorrelation.
D) interaction.
A) leverage.
B) multicorrelation.
C) autocorrelation.
D) interaction.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
18
In multiple regression analysis, the word linear in the term "general linear model" refers to the fact that β0, β1, . . ., βp all have exponents of
A) 0.
B) 1.
C) at least 1.
D) less than 0.
A) 0.
B) 1.
C) at least 1.
D) less than 0.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
19
The range of the Durbin-Watson statistic is from
A) -1 to 1.
B) 0 to 1.
C) -∞ to +∞.
D) 0 to 4.
A) -1 to 1.
B) 0 to 1.
C) -∞ to +∞.
D) 0 to 4.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following tests is used to determine whether an additional variable makes a significant contribution to a multiple regression model?
A) a t test
B) a z test
C) an F test
D) a chi-square test
A) a t test
B) a z test
C) an F test
D) a chi-square test

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
21
A regression model with one independent variable, x1, resulted in an SSE of 50. When a second independent variable, x2, was added to the model, the SSE was reduced to 40. At α = .05, determine if x2 contributes significantly to the model. The sample size for both models was 30.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
22
When a regression model was developed relating sales (y) of a company to its product's price (x1), the SSE was determined to be 495. A second regression model relating sales (y) to product's price (x1) and competitor's product's price (x2) resulted in an SSE of 396. At α = .05, determine if the competitor's product's price contributed significantly to the model. The sample size for both models was 33.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
23
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 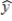 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained. The multiple coefficient of determination is
The multiple coefficient of determination is
A) .23.
B) .74.
C) .50.
D) .33.
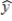 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
 The multiple coefficient of determination is
The multiple coefficient of determination isA) .23.
B) .74.
C) .50.
D) .33.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
24
Which of the following variable selection procedures would be considered non-heuristic
A) forward selection.
B) backward elimination.
C) best-subsets regression.
D) stepwise regression.
A) forward selection.
B) backward elimination.
C) best-subsets regression.
D) stepwise regression.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
25
Thirty-four observations of a dependent variable and two independent variables resulted in an SSE of 300. When a third independent variable was added to the model, the SSE was reduced to 250. Using α = .05, determine whether or not the third independent variable contributes significantly to the model.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
26
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 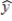 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
The test statistic for testing the significance of the model is
A) .73.
B) 18.93.
C) 19.47.
D) 1.37.
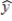 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
The test statistic for testing the significance of the model is
A) .73.
B) 18.93.
C) 19.47.
D) 1.37.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
27
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 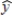 = 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
= 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.  If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model), the critical value of F at α = .05 is
If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model), the critical value of F at α = .05 is
A) 2.76.
B) 4.87.
C) 3.10.
D) 3.07.
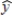 = 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.
= 12 - 18x1 + 4x2 + 15x3 Also, the following standard errors and the sum of squares were obtained.  If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model), the critical value of F at α = .05 is
If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model), the critical value of F at α = .05 isA) 2.76.
B) 4.87.
C) 3.10.
D) 3.07.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
28
A researcher is trying to decide whether or not to add another variable to his regression model. He has estimated the following equation for the model from a sample of 28 observations. 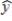 = 23.62 + 18.86x1 + 24.72x2
= 23.62 + 18.86x1 + 24.72x2
SSE = 1425
SSR = 1320
He has also estimated the model with an additional variable x3. The results are: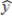 = 25.32 + 15.29x1 + 7.63x2 + 12.72x3
= 25.32 + 15.29x1 + 7.63x2 + 12.72x3
SSE = 1350
SSR = 1465
What advice would you give this researcher? Use a .10 level of significance.
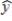 = 23.62 + 18.86x1 + 24.72x2
= 23.62 + 18.86x1 + 24.72x2SSE = 1425
SSR = 1320
He has also estimated the model with an additional variable x3. The results are:
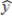 = 25.32 + 15.29x1 + 7.63x2 + 12.72x3
= 25.32 + 15.29x1 + 7.63x2 + 12.72x3SSE = 1350
SSR = 1465
What advice would you give this researcher? Use a .10 level of significance.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
29
Using the Durbin-Watson test for negative autocorrelation, we conclude that negative autocorrelation is present if
A) d > 4 - dL.
B) d < dL.
C) d < dU.
D) d < 4 - dU.
A) d > 4 - dL.
B) d < dL.
C) d < dU.
D) d < 4 - dU.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
30
In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 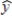 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
The p-value for testing the significance of the regression model is
A) less than .01.
B) between .01 and .025.
C) between .025 and .05.
D) greater than .10.
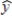 = 12 - 18x1 + 4x2 + 15x3
= 12 - 18x1 + 4x2 + 15x3
Also, the following standard errors and the sum of squares were obtained.
Sb1 = 3
Sb2 = 6
Sb3 = 7
SST = 4900
SSE = 1296
The p-value for testing the significance of the regression model is
A) less than .01.
B) between .01 and .025.
C) between .025 and .05.
D) greater than .10.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following statements about the backward elimination procedure is false?
A) It is a one-variable-at-a-time procedure.
B) It begins with the regression model found using the forward selection procedure.
C) It does not permit an independent variable to be reentered once it has been removed.
D) It does not guarantee that the best regression model will be found.
A) It is a one-variable-at-a-time procedure.
B) It begins with the regression model found using the forward selection procedure.
C) It does not permit an independent variable to be reentered once it has been removed.
D) It does not guarantee that the best regression model will be found.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
32
A data set consisting of 7 observations of a dependent variable y and two independent variables x1 and x2 was used in a regression analysis. Using x1 as the only independent variable, the following function is provided. 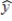 = .408 + 1.338x1
= .408 + 1.338x1
The SSE for the above model is 39.535.
Using both x1 and x2 as independent variables yields the following function.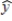 = .805 + .498x1 - .477x2
= .805 + .498x1 - .477x2
The SSE for this function is 1.015.
Use an F test and determine if x2 contributes significantly to the model. Let α = .10.
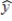 = .408 + 1.338x1
= .408 + 1.338x1The SSE for the above model is 39.535.
Using both x1 and x2 as independent variables yields the following function.
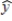 = .805 + .498x1 - .477x2
= .805 + .498x1 - .477x2The SSE for this function is 1.015.
Use an F test and determine if x2 contributes significantly to the model. Let α = .10.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
33
An example of a first-order model with three predictor variables is
A) y = 0 + 1x1 + 2x2 + 3x3 +
B) y = 0 + 1x1 + 2x2 +
C) y = 0 + 1x2 + 3x3+
D) y2 = 0 + 1x1 + 2x2+ 3x3 + .
A) y = 0 + 1x1 + 2x2 + 3x3 +
B) y = 0 + 1x1 + 2x2 +
C) y = 0 + 1x2 + 3x3+
D) y2 = 0 + 1x1 + 2x2+ 3x3 + .

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
34
A regression analysis involving 45 observations relating a dependent variable and two independent variables resulted in the following information.
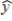 = .408 + 1.3387x1 + 2x2
= .408 + 1.3387x1 + 2x2
The SSE for the above model is 49. When two other independent variables were added to the model, the following information was provided.
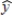 = 1.2 + 3x1 + 12x2 + 4x3 + 8x4
= 1.2 + 3x1 + 12x2 + 4x3 + 8x4
This model's SSE is 40.
At a .05 level of significance, test to determine if the two added independent variables contribute significantly to the model.
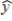 = .408 + 1.3387x1 + 2x2
= .408 + 1.3387x1 + 2x2
The SSE for the above model is 49. When two other independent variables were added to the model, the following information was provided.
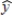 = 1.2 + 3x1 + 12x2 + 4x3 + 8x4
= 1.2 + 3x1 + 12x2 + 4x3 + 8x4
This model's SSE is 40.
At a .05 level of significance, test to determine if the two added independent variables contribute significantly to the model.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
35
In order to use the output from a multiple regression analysis to perform the ANOVA test on the difference among the means of four populations, how many dummy variables are needed to indicate treatments?
A) 1
B) 2
C) 3
D) 4
A) 1
B) 2
C) 3
D) 4

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
36
When autocorrelation is present, one of the assumptions of the regression model is violated and that assumption is?
A) ?the expected value of the error term is zero.
B) ?the variance of the error term is the same for all values of x.
C) ?the values of the error term are independent.
D) ?the values of the error term are normally distributed for all values of x.
A) ?the expected value of the error term is zero.
B) ?the variance of the error term is the same for all values of x.
C) ?the values of the error term are independent.
D) ?the values of the error term are normally distributed for all values of x.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
37
The null hypothesis in the Durbin-Watson test is always that there is
A) H0: ρ > 0.
B) H0: ρ < 0.
C) H0: ρ ≠ 0.
D) H0: ρ = 0.
A) H0: ρ > 0.
B) H0: ρ < 0.
C) H0: ρ ≠ 0.
D) H0: ρ = 0.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
38
A regression model relating a dependent variable, y, with one independent variable, x1, resulted in an SSE of 400. Another regression model with the same dependent variable, y, and two independent variables, x1 (used in the first model) and x2 (added in the second model), resulted in an SSE of 320. At α = .05, determine if x2 contributed significantly to the model. The sample size for both models was 20.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
39
The variable selection procedure that identifies the best regression model, given a specified number of independent variables, is
A) stepwise regression.
B) forward selection.
C) backward elimination.
D) best-subsets regression.
A) stepwise regression.
B) forward selection.
C) backward elimination.
D) best-subsets regression.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
40
The forward selection procedure starts with _____ independent variable(s) in the multiple regression model.
A) no
B) one
C) two
D) all
A) no
B) one
C) two
D) all

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
41
Forty-eight observations of a dependent variable and five independent variables resulted in an SSE of 438. When two additional independent variables were added to the model, the SSE was reduced to 375. At a 5% level of significance, determine whether or not the two added independent variables contribute significantly to the model.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck


