Exam 16: Regression Analysis: Model Building

When a regression model was developed relating sales (y) of a company to its product's price (x₁), the SSE was determined to be 495. A second regression model relating sales (y) to product's price (x₁) and competitor's product's price (x₂) resulted in an SSE of 396. At α = .05, determine if the competitor's product's price contributed significantly to the model. The sample size for both models was 33.

The null hypothesis in the Durbin-Watson test is always that there is

An example of a first-order model with three predictor variables is

Thirty-four observations of a dependent variable and two independent variables resulted in an SSE of 300. When a third independent variable was added to the model, the SSE was reduced to 250. Using α = .05, determine whether or not the third independent variable contributes significantly to the model.

In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. ​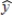 = 12 - 18x₁ + 4x₂ + 15x₃ ​ Also, the following standard errors and the sum of squares were obtained. S_b1 = 3 S_b2 = 6 S_b3 = 7 SST = 4900 SSE = 1296 At the .01 level of significance, the coefficient of x₃

All the independent variables in a multiple regression analysis

When dealing with the problem of nonconstant variance, the reciprocal transformation means using

The forward selection procedure starts with _____ independent variable(s) in the multiple regression model.

In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. 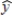= 12 - 18x₁ + 4x₂ + 15x₃ Also, the following standard errors and the sum of squares were obtained. If we are interested in testing for the significance of the relationship among the variables (i.e., significance of the model), the critical value of F at α = .05 is

In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was develop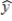ed. ​ = 12 - 18x₁ + 4x₂ + 15x₃ ​ Also, the following standard errors and the sum of squares were obtained. The multiple coefficient of determination is

In a regression analysis of a first-order model involving 3 predictor variables and 25 observations, the following estimated regression equation was developed. ​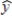 = 12 - 18x₁ + 4x₂ + 15x₃ ​ Also, the following standard errors and the sum of squares were obtained. ​ S_b1 = 3 S_b2 = 6 S_b3 = 7 SST = 4900 SSE = 1296 ​ The p-value for testing the significance of the regression model is

Models in which the parameters have exponents other than 1 are called

A data set consisting of 7 observations of a dependent variable y and two independent variables x₁ and x₂ was used in a regression analysis. Using x₁ as the only independent variable, the following function is provided. 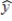= .408 + 1.338x₁ The SSE for the above model is 39.535. Using both x₁ and x₂ as independent variables yields the following function. 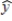= .805 + .498x₁ - .477x₂ The SSE for this function is 1.015. Use an F test and determine if x₂ contributes significantly to the model. Let α = .10.

In multiple regression analysis, the word linear in the term "general linear model" refers to the fact that β₀, β₁, . . ., βp all have exponents of

The following regression model ​ Y = β₀ + β₁x₁ + β₂ 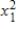+ ε ​is known as a

The correlation in error terms that arises when the error terms at successive points in time are related is termed

Serial correlation is

When autocorrelation is present, one of the assumptions of the regression model is violated and that assumption is?

In multiple regression analysis, the general linear model

Which of the following variable selection procedures would be considered non-heuristic