Deck 2: Key Concept: the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 2: Key Concept: the Derivative
1
The length, x, of the side of a cube with volume V is given by 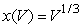 .Is the average rate of change of x with respect to V increasing or decreasing as the volume V decreases?
.Is the average rate of change of x with respect to V increasing or decreasing as the volume V decreases?
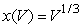 .Is the average rate of change of x with respect to V increasing or decreasing as the volume V decreases?
.Is the average rate of change of x with respect to V increasing or decreasing as the volume V decreases?increasing
2
A runner planned her strategy for running a half marathon, a distance of 13.1 miles.She planned to run negative splits, faster speeds as time passed during the race.In the actual race, she ran the first 6 miles in 48 minutes, the second 4 miles in 28 minutes and the last 3.1 miles in 18 minutes.What was her average velocity over the first 6 miles? What was her average velocity over the entire race? Did she run negative splits?
A)7.50 mph for the first 5 miles, 8.36 mph for the race, No
B)8.36 mph for the first 5 miles, 7.50 mph for the race, No
C)8.12 mph for the first 5 miles, 7.35 mph for the race, Yes
D)7.35 mph for the first 5 miles, 8.12 mph for the race, No
A)7.50 mph for the first 5 miles, 8.36 mph for the race, No
B)8.36 mph for the first 5 miles, 7.50 mph for the race, No
C)8.12 mph for the first 5 miles, 7.35 mph for the race, Yes
D)7.35 mph for the first 5 miles, 8.12 mph for the race, No
7.50 mph for the first 5 miles, 8.36 mph for the race, No
3
Estimate 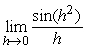 to 2 decimal places by substituting smaller and smaller values of h (use radians).
to 2 decimal places by substituting smaller and smaller values of h (use radians).
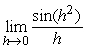 to 2 decimal places by substituting smaller and smaller values of h (use radians).
to 2 decimal places by substituting smaller and smaller values of h (use radians).0
4
Given the following data about a function f, estimate 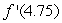 .
.
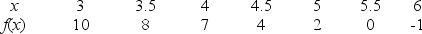
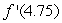 .
.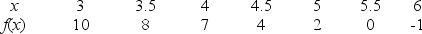

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
The height of an object in feet above the ground is given in the following table.If heights of the object are cut in half, how does the average velocity change, over a given interval? 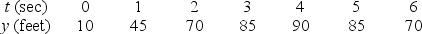
A)It is cut in half.
B)It is doubled.
C)It remains the same.
D)It depends on the interval.
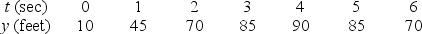
A)It is cut in half.
B)It is doubled.
C)It remains the same.
D)It depends on the interval.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
If 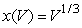 is the length of the side of a cube in terms of its volume, V, calculate the average rate of change of x with respect to V over the interval
is the length of the side of a cube in terms of its volume, V, calculate the average rate of change of x with respect to V over the interval 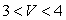 to 2 decimal places.
to 2 decimal places.
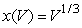 is the length of the side of a cube in terms of its volume, V, calculate the average rate of change of x with respect to V over the interval
is the length of the side of a cube in terms of its volume, V, calculate the average rate of change of x with respect to V over the interval 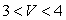 to 2 decimal places.
to 2 decimal places.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
The height of an object in feet above the ground is given in the following table, 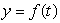 .Make a graph of
.Make a graph of 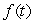 .On your graph , what does the average velocity over a the interval
.On your graph , what does the average velocity over a the interval 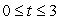 represent?
represent? 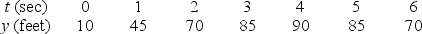
A)The average height between f(0)and f(3).
B)The slope of the line between the points (0, f(0)), and (3, f(3)).
C)The average of the slopes of the tangent lines to the points (0, f(0)), and (3, f(3)).
D)The distance between the points (0, f(0)), and (3, f(3)).
 .Make a graph of
.Make a graph of  .On your graph , what does the average velocity over a the interval
.On your graph , what does the average velocity over a the interval 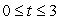 represent?
represent? 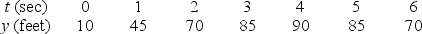
A)The average height between f(0)and f(3).
B)The slope of the line between the points (0, f(0)), and (3, f(3)).
C)The average of the slopes of the tangent lines to the points (0, f(0)), and (3, f(3)).
D)The distance between the points (0, f(0)), and (3, f(3)).

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
Given the following table of values for a Bessel function, 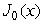 , estimate the derivative at x = 0.5.
, estimate the derivative at x = 0.5.
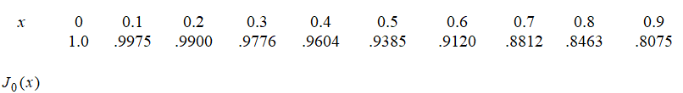
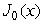 , estimate the derivative at x = 0.5.
, estimate the derivative at x = 0.5.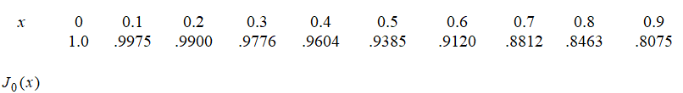

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
The data in the table report the average improvement in scores of six college freshmen who took a writing assessment before and again after they had x hours of tutoring by a tutor trained in a new method of instruction.When f(x)>0 the group showed improvement on average.
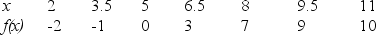 a)Find the average change in score from 6.5 to 9.5 hours of tutoring.
a)Find the average change in score from 6.5 to 9.5 hours of tutoring.
b)Estimate the instantaneous rate of change at 8 hours.
c)Approximate the equation of the tangent line at x = 8 hours.
d)Use the tangent line to estimate f(8.5).
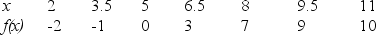 a)Find the average change in score from 6.5 to 9.5 hours of tutoring.
a)Find the average change in score from 6.5 to 9.5 hours of tutoring.b)Estimate the instantaneous rate of change at 8 hours.
c)Approximate the equation of the tangent line at x = 8 hours.
d)Use the tangent line to estimate f(8.5).

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
There is a function used by statisticians, called the error function, which is written y = erf (x).Suppose you have a statistical calculator, which has a button for this function.Playing with your calculator, you discover the following:
Using this information alone, give an estimate for erf'(0), the derivative of erf at x = 0 to 4 decimal places.
Using this information alone, give an estimate for erf'(0), the derivative of erf at x = 0 to 4 decimal places.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Given the following data about a function f(x), the equation of the tangent line at x = 5 is approximated by 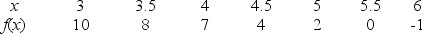
A)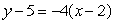
B)
C)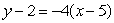
D)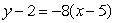
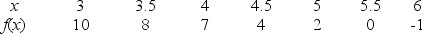
A)
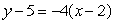
B)

C)
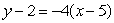
D)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
A horticulturist conducted an experiment to determine the effects of different amounts of fertilizer on the yield of a plot of green onions.He modeled his results with the function 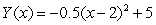 where Y is the yield in bushels and x is the amount of fertilizer in pounds.What are
where Y is the yield in bushels and x is the amount of fertilizer in pounds.What are 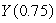 and
and 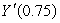 ? Give your answers to two decimal places, specify units.
? Give your answers to two decimal places, specify units.
A)4.22 bushels, 1.25 bushels/pound, respectively
B)4.22 bushels, 6.25 bushels/pound, respectively
C)1.25 bushels, 1.56 bushels/pound, respectively
D)1.25 bushels, 4.22 bushels/pound, respectively
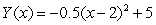 where Y is the yield in bushels and x is the amount of fertilizer in pounds.What are
where Y is the yield in bushels and x is the amount of fertilizer in pounds.What are 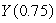 and
and 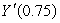 ? Give your answers to two decimal places, specify units.
? Give your answers to two decimal places, specify units.A)4.22 bushels, 1.25 bushels/pound, respectively
B)4.22 bushels, 6.25 bushels/pound, respectively
C)1.25 bushels, 1.56 bushels/pound, respectively
D)1.25 bushels, 4.22 bushels/pound, respectively

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
For
, estimate f '(3)to 3 decimal places by finding the average slope over intervals containing the value x = 3.
, estimate f '(3)to 3 decimal places by finding the average slope over intervals containing the value x = 3.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Let 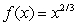 .Use a graph to decide which one of the following statements is true.
.Use a graph to decide which one of the following statements is true.
A)When x = -5, the derivative is negative; when x = 5, the derivative is positive; and as x approaches infinity, the derivative approaches 0.
B)When x = -6, the derivative is positive; when x = 6, the derivative is also positive, and as x approaches infinity, the derivative approaches 0.
C)When x = -7, the derivative is negative; when x = 7, the derivative is positive, and as x approaches infinity, the derivative approaches infinity.
D)The derivative is positive at at all values of x.
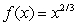 .Use a graph to decide which one of the following statements is true.
.Use a graph to decide which one of the following statements is true.A)When x = -5, the derivative is negative; when x = 5, the derivative is positive; and as x approaches infinity, the derivative approaches 0.
B)When x = -6, the derivative is positive; when x = 6, the derivative is also positive, and as x approaches infinity, the derivative approaches 0.
C)When x = -7, the derivative is negative; when x = 7, the derivative is positive, and as x approaches infinity, the derivative approaches infinity.
D)The derivative is positive at at all values of x.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
For 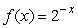 , estimate
, estimate 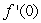 to 3 decimal places.
to 3 decimal places.
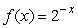 , estimate
, estimate 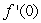 to 3 decimal places.
to 3 decimal places.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
Let f(x)= log(log(x)).Estimate 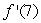 to 3 decimal places using any method.
to 3 decimal places using any method.
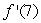 to 3 decimal places using any method.
to 3 decimal places using any method.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Use the graph of 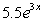 at the point (0, 5.5)to estimate
at the point (0, 5.5)to estimate 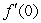 to three decimal places.
to three decimal places.
A)16.500
B)36.823
C)3.500
D)146.507
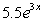 at the point (0, 5.5)to estimate
at the point (0, 5.5)to estimate 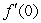 to three decimal places.
to three decimal places.A)16.500
B)36.823
C)3.500
D)146.507

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
For any number r, let m(r)be the slope of the graph of the function 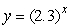 at the point x = r.Estimate m(4)to 2 decimal places.
at the point x = r.Estimate m(4)to 2 decimal places.
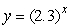 at the point x = r.Estimate m(4)to 2 decimal places.
at the point x = r.Estimate m(4)to 2 decimal places.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
The height of an object in feet above the ground is given in the following table.Compute the average velocity over the interval 1 t 3.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
Estimate 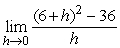 to 2 decimal places by substituting smaller and smaller values of h.
to 2 decimal places by substituting smaller and smaller values of h.
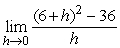 to 2 decimal places by substituting smaller and smaller values of h.
to 2 decimal places by substituting smaller and smaller values of h.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Estimate a formula for 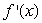 for the function
for the function 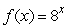 .Round constants to 3 decimal places.
.Round constants to 3 decimal places.
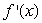 for the function
for the function 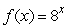 .Round constants to 3 decimal places.
.Round constants to 3 decimal places.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
To find the derivative of 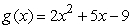 at x = 8 algebraically, you evaluate the following expression.
at x = 8 algebraically, you evaluate the following expression.
A)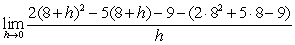
B)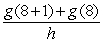
C)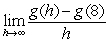
D)All of the above are correct.
E)None of the above is correct.
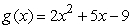 at x = 8 algebraically, you evaluate the following expression.
at x = 8 algebraically, you evaluate the following expression.A)
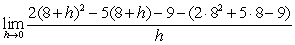
B)
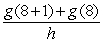
C)
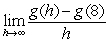
D)All of the above are correct.
E)None of the above is correct.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
Could the first graph, A be the derivative of the second graph, B? 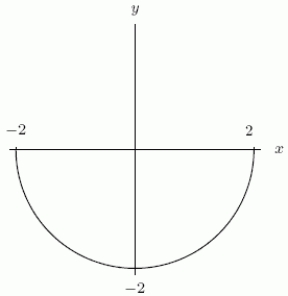
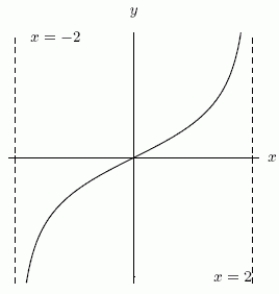 A B
A B

 A B
A B
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
To study traffic flow along a major road, the city installs a device at the edge of the road at 1:00a.m.The device counts the cars driving past, and records the total periodically.The resulting data is plotted on a graph, with time (in hours since installation)on the horizontal axis and the number of cars on the vertical axis.The graph is shown below; it is the graph of the function C(t)= Total number of cars that have passed by after t hours.When is the traffic flow greatest? 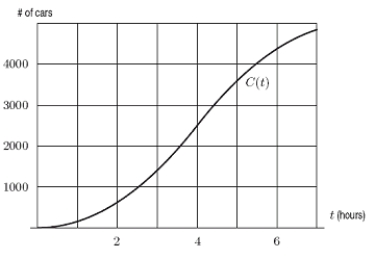
A)2:00 am
B)3:00 am
C)4:00 am
D)5:00 am

A)2:00 am
B)3:00 am
C)4:00 am
D)5:00 am

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
The graph below shows the velocity of a bug traveling along a straight line on the classroom floor. 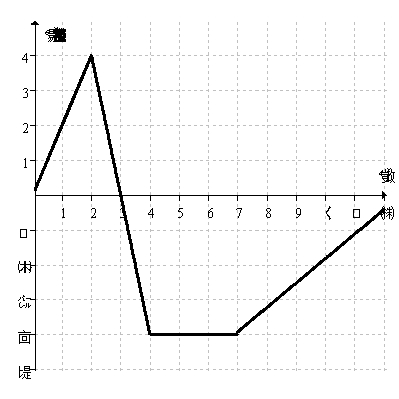 At what time(s)does the bug turn around?
At what time(s)does the bug turn around?
A)At 3 seconds.
B)At 2 seconds and again at 7 seconds.
C)At 4 seconds and again at 7 seconds.
D)Never.
 At what time(s)does the bug turn around?
At what time(s)does the bug turn around?A)At 3 seconds.
B)At 2 seconds and again at 7 seconds.
C)At 4 seconds and again at 7 seconds.
D)Never.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Draw the graph of a continuous function y = g(x)that satisfies the following three conditions:
• g'(x)= 0 for x < 0
• g'(x)> 0 for 0 < x < 4
• g'(x)< 0 for x > 4
• g'(x)= 0 for x < 0
• g'(x)> 0 for 0 < x < 4
• g'(x)< 0 for x > 4

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
Find the derivative of 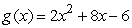 at x = 4 algebraically.
at x = 4 algebraically.
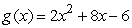 at x = 4 algebraically.
at x = 4 algebraically.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
he graph below shows the velocity of a bug traveling along a straight line on the classroom floor. 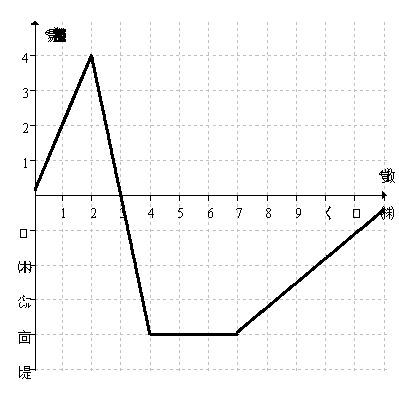 Graph the bug's speed at time, t.How does it differ from the bug's velocity?
Graph the bug's speed at time, t.How does it differ from the bug's velocity?
 Graph the bug's speed at time, t.How does it differ from the bug's velocity?
Graph the bug's speed at time, t.How does it differ from the bug's velocity?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
Find the derivative of 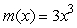 at x = 1 algebraically.
at x = 1 algebraically.
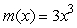 at x = 1 algebraically.
at x = 1 algebraically.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
Could the first graph, A be the derivative of the second graph, B? 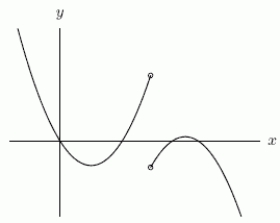
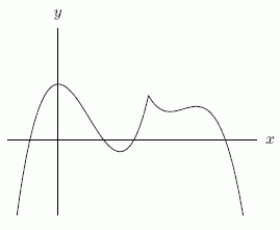 A B
A B

 A B
A B
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Use the limit of the difference quotient to find the derivative of 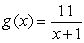 at the point (1, 11/2).
at the point (1, 11/2).
A)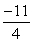
B)
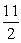
C)-11
D)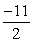
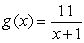 at the point (1, 11/2).
at the point (1, 11/2).A)
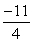
B)

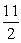
C)-11
D)
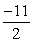

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
To study traffic flow along a major road, the city installs a device at the edge of the road at 3:00a.m.The device counts the cars driving past, and records the total periodically.The resulting data is plotted on a graph, with time (in hours since installation)on the horizontal axis and the number of cars on the vertical axis.The graph is shown below; it is the graph of the function C(t)= Total number of cars that have passed by after t hours.From the graph, estimate C'(6). 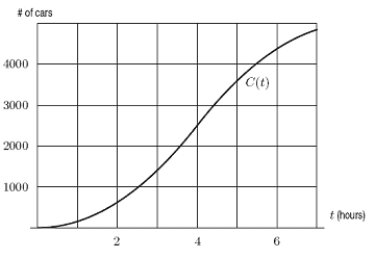
A)600
B)900
C)1200
D)1500

A)600
B)900
C)1200
D)1500

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
A runner competed in a half marathon in Anaheim, a distance of 13.1 miles.She ran the first 7 miles at a steady pace in 48 minutes, the second 3 miles at a steady pace in 28 minutes and the last 3.1 miles at a steady pace in 18 minutes.
a)Sketch a well-labeled graph of her distance completed with respect to time.
b)Sketch a well-labeled graph of her velocity with respect to time.
a)Sketch a well-labeled graph of her distance completed with respect to time.
b)Sketch a well-labeled graph of her velocity with respect to time.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
The definition of the derivative function is 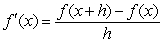
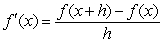

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose that f(T)is the cost to heat my house, in dollars per day, when the outside temperature is T .If f(28)= 11.10 and f '(28)= -0.12, approximately what is the cost to heat my house when the outside temperature is 25 ?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
The graph below shows the velocity of a bug traveling along a straight line on the classroom floor. 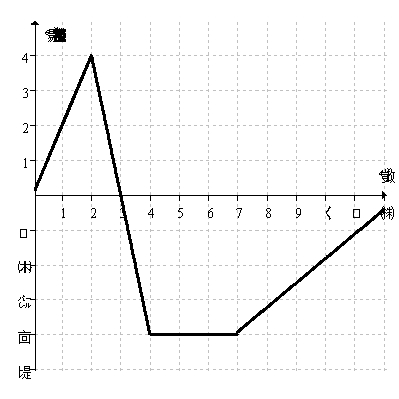 When is the bug moving at a constant speed?
When is the bug moving at a constant speed?
A)Between 4 and 7 seconds.
B)Whenever the velocity is linear with a positive slope.
C)Whenever the velocity is linear with a negative slope.
D)When the velocity is equal to zero.
 When is the bug moving at a constant speed?
When is the bug moving at a constant speed?A)Between 4 and 7 seconds.
B)Whenever the velocity is linear with a positive slope.
C)Whenever the velocity is linear with a negative slope.
D)When the velocity is equal to zero.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
Use the definition of the derivative function to find a formula for the slope of the graph of 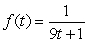 .
.
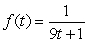 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
What is the equation of the tangent line to the graph of 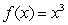 at the point (2, 8)?
at the point (2, 8)?
A)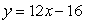
B)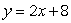
C)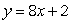
D)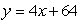
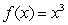 at the point (2, 8)?
at the point (2, 8)?A)
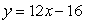
B)
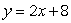
C)
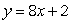
D)
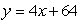

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
Could the first graph, A be the derivative of the second graph, B? 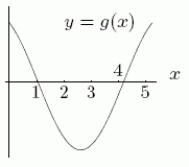
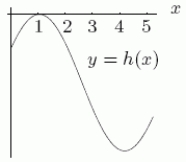 A B
A B

 A B
A B
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
Consider the function y = f(x)graphed below.At the point x = -3, is 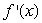 positive, negative, 0, or undefined?Note: f(x)is defined for -5 < x < 6, except x = 2.
positive, negative, 0, or undefined?Note: f(x)is defined for -5 < x < 6, except x = 2. 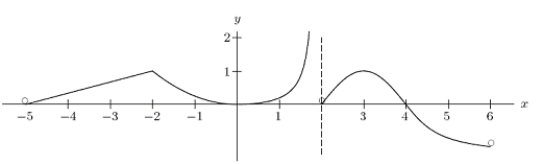
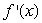 positive, negative, 0, or undefined?Note: f(x)is defined for -5 < x < 6, except x = 2.
positive, negative, 0, or undefined?Note: f(x)is defined for -5 < x < 6, except x = 2. 

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
A function defined for all x has the following properties:
• f is increasing
• f is concave down
• f (3)= 2
• f '(3)= 1/2
How many zeros does f(x)have in the interval
?
• f is increasing
• f is concave down
• f (3)= 2
• f '(3)= 1/2
How many zeros does f(x)have in the interval
?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
The graph below represents the rate of change of a function f with respect to x; i.e., it is a graph of f '.You are told that f (0)= 0.What can you say about
at the point x = 1.3? Mark all that apply.
A) is decreasing.
B)
is increasing.
C)
is concave up.
D)
is concave down.
at the point x = 1.3? Mark all that apply.

A) is decreasing.
B)
is increasing.
C)
is concave up.
D)
is concave down.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Let L(r)be the amount of board-feet of lumber produced from a tree of radius r (measured in inches).What does L(16)mean in practical terms?
A)The amount of board-feet of lumber produced from a tree with a radius of 16 inches.
B)The radius of a tree that will produce 16 board-feet of lumber.
C)The rate of change of the amount of lumber with respect to radius when the radius is 16 inches (in board-feet per inch).
D)The rate of change of the radius with respect to the amount of lumber produced when the amount is 16 board-feet (in inches per board-foot).
A)The amount of board-feet of lumber produced from a tree with a radius of 16 inches.
B)The radius of a tree that will produce 16 board-feet of lumber.
C)The rate of change of the amount of lumber with respect to radius when the radius is 16 inches (in board-feet per inch).
D)The rate of change of the radius with respect to the amount of lumber produced when the amount is 16 board-feet (in inches per board-foot).

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
The graph of  is given in the following figure.What happens to
is given in the following figure.What happens to 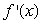 at the point
at the point 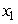 ?
? 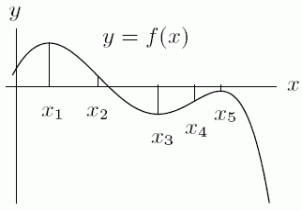

A)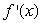 has an inflection point.
has an inflection point.
B)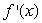 has a local minimum or maximum.
has a local minimum or maximum.
C)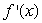 changes sign.
changes sign.
D)none of the above
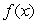 is given in the following figure.What happens to
is given in the following figure.What happens to 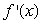 at the point
at the point 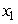 ?
? 

A)
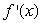 has an inflection point.
has an inflection point.B)
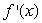 has a local minimum or maximum.
has a local minimum or maximum.C)
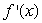 changes sign.
changes sign.D)none of the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
The graph below gives the position of a spider moving along a straight line on the forest floor for 10 seconds.On the same axes, sketch a graph of the spider's velocity over the 10 seconds.Then write a description of the spider's movement for the 10 second period. 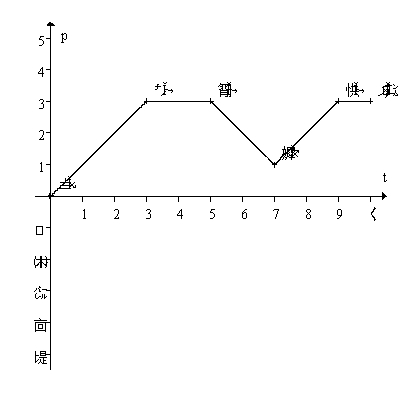


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
Esther is a swimmer who prides herself in having a smooth backstroke.Let s(t)be her position in an Olympic size (50-meter)pool, as a function of time (s(t)is measured in meters, t is seconds).Below we list some values of s(t), for a recent swim.Based on the data, was Esther's instantaneous speed ever greater than 3 meters/second?
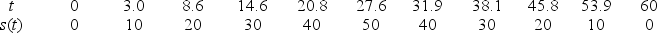
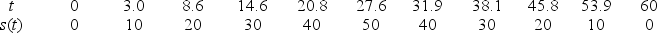

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Given the following data about a function f, estimate the rate of change of the derivative  at x = 4.5.
at x = 4.5.
.
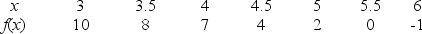
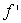 at x = 4.5.
at x = 4.5..

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Let t(h)be the temperature in degrees Celsius at a height h (in meters)above the surface of the earth.What does t '(1200)mean in practical terms?
A)The temperature in degrees Celsius at a height 1200 meters above the surface of the earth.
B)The height above the surface of the earth at which the temperature is 1200 degrees Celsius.
C)The rate of change of temperature with respect to height at 1200 meters above the surface of the earth (in degrees per meter).
D)The rate of change of height with respect to temperature when the temperature is 1200 degrees Celsius (in meters per degree).
A)The temperature in degrees Celsius at a height 1200 meters above the surface of the earth.
B)The height above the surface of the earth at which the temperature is 1200 degrees Celsius.
C)The rate of change of temperature with respect to height at 1200 meters above the surface of the earth (in degrees per meter).
D)The rate of change of height with respect to temperature when the temperature is 1200 degrees Celsius (in meters per degree).

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
On the axes below, sketch a smooth, continuous curve , and which clearly satisfies the following conditions:
• Concave up to the left of P
• Concave down to the right of P
• Increasing for x > 0
• Decreasing for x < 0
• Does not pass through the origin.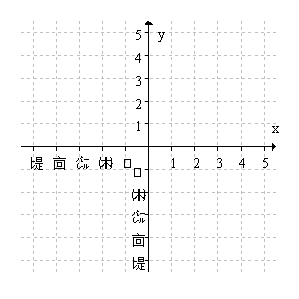
• Concave up to the left of P
• Concave down to the right of P
• Increasing for x > 0
• Decreasing for x < 0
• Does not pass through the origin.


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
Every day the Office of Undergraduate Admissions receives inquiries from eager high school students.They keep a running account of the number of inquiries received each day, along with the total number received until that point.Below is a table of weekly figures from about the end of August to about the end of October of a recent year.
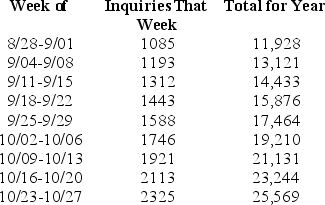 Based on the table determine a formula that approximates the total number of inquiries received by a given week.Use your formula to estimate how many inquiries the admissions office will have received by November 24.
Based on the table determine a formula that approximates the total number of inquiries received by a given week.Use your formula to estimate how many inquiries the admissions office will have received by November 24.
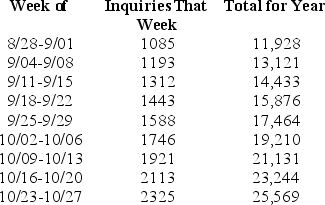 Based on the table determine a formula that approximates the total number of inquiries received by a given week.Use your formula to estimate how many inquiries the admissions office will have received by November 24.
Based on the table determine a formula that approximates the total number of inquiries received by a given week.Use your formula to estimate how many inquiries the admissions office will have received by November 24.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
The cost in dollars to produce q bottles of a prescription skin treatment is given by the function 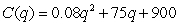 .The manufacturing process is difficult and costly when large quantities are produced.The marginal cost of producing one additional bottle when q bottles have been produced is the derivative
.The manufacturing process is difficult and costly when large quantities are produced.The marginal cost of producing one additional bottle when q bottles have been produced is the derivative 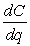 .
.
a)Find the marginal cost function.
b)Compute C(50)and explain what the number means in terms of cost and production.
c)Compute C'(50)and explain what the number means in terms of cost and production.
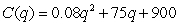 .The manufacturing process is difficult and costly when large quantities are produced.The marginal cost of producing one additional bottle when q bottles have been produced is the derivative
.The manufacturing process is difficult and costly when large quantities are produced.The marginal cost of producing one additional bottle when q bottles have been produced is the derivative 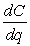 .
.a)Find the marginal cost function.
b)Compute C(50)and explain what the number means in terms of cost and production.
c)Compute C'(50)and explain what the number means in terms of cost and production.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Let t(h)be the temperature in degrees Celsius at a height of h meters above the surface of the earth.What does t(h)+ 15 mean in practical terms?
A)The temperature in degrees Celsius at a height h meters above the surface of the earth plus an additional 15 degrees
B)The height above the surface of the earth at which the temperature is h degrees Celsius plus an additional 15 meters.
C)The rate of change of temperature with respect to height at 15 additional meters above the surface of the earth (in degrees per meter).
D)The rate of change of height with respect to temperature when the temperature is 15 additional degrees Celsius (in meters per degree).
A)The temperature in degrees Celsius at a height h meters above the surface of the earth plus an additional 15 degrees
B)The height above the surface of the earth at which the temperature is h degrees Celsius plus an additional 15 meters.
C)The rate of change of temperature with respect to height at 15 additional meters above the surface of the earth (in degrees per meter).
D)The rate of change of height with respect to temperature when the temperature is 15 additional degrees Celsius (in meters per degree).

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
The graph below represents the rate of change of a function f with respect to x; i.e., it is a graph of f'.You are told that f(0)= -2.For approximately what value of x other than x = 0 in the interval 0 x 2 does
= -2?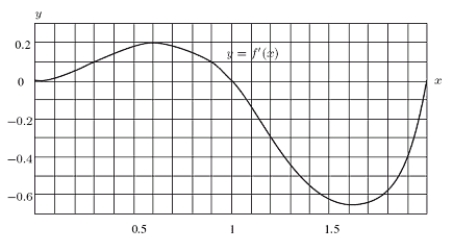
A)0.6
B)1
C)1.4
D)2
E)None of the above
= -2?

A)0.6
B)1
C)1.4
D)2
E)None of the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
A concert promoter estimates that the cost of printing p full color posters for a major concert is given by a function Cost = c(p)where p is the number of posters produced.
a)Interpret the meaning of the statement c(450)= 5400.
b)Interpret the meaning of the statement c'(450)= 11.
a)Interpret the meaning of the statement c(450)= 5400.
b)Interpret the meaning of the statement c'(450)= 11.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
Esther is a swimmer who prides herself in having a smooth backstroke.Let s(t)be her position in an Olympic size (50-meter)pool, as a function of time (s(t)is measured in meters, t is seconds).Below we list some values of s(t)for a recent swim.Find Esther's average speed over the entire swim in meters per second.Round to 2 decimal places.
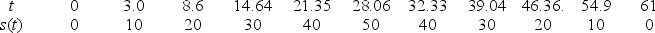
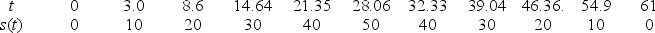

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
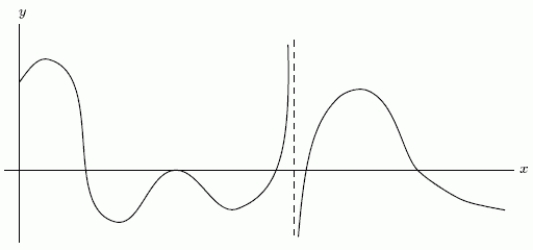
One of the following graphs is of 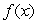 , and the other is of
, and the other is of 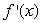 .Is
.Is 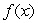 the first graph or the second graph?
the first graph or the second graph? 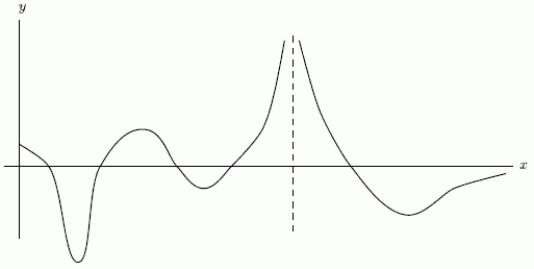
 , and the other is of
, and the other is of  .Is
.Is 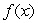 the first graph or the second graph?
the first graph or the second graph? 


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
Let t(h)be the temperature in degrees Celsius at a height of h meters above the surface of the earth.What does h such that t(h)= 8 mean in practical terms?
A)The temperature in degrees Celsius at a height 8 meters above the surface of the earth.
B)The height above the surface of the earth at which the temperature is 8 degrees Celsius.
C)The rate of change of temperature with respect to height at 8 meters above the surface of the earth (in degrees per meter).
D)The rate of change of height with respect to temperature when the temperature is 8 degrees Celsius (in meters per degree).
A)The temperature in degrees Celsius at a height 8 meters above the surface of the earth.
B)The height above the surface of the earth at which the temperature is 8 degrees Celsius.
C)The rate of change of temperature with respect to height at 8 meters above the surface of the earth (in degrees per meter).
D)The rate of change of height with respect to temperature when the temperature is 8 degrees Celsius (in meters per degree).

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
A typhoon is a tropical cyclone, like a hurricane, that forms in the northwestern Pacific Ocean.The wind speed of a typhoon is given by a function W = w(r)where W is measured in meters/sec., and r is measured in kilometers from the center of the typhoon.What does the statement that w'(15)> 0 tell you about the typhoon?
A)At a distance of 15 kilometers from the center of the typhoon, the wind speed is increasing.
B)At a distance of 15 kilometers from the center of the typhoon, the wind speed is positive.
C)The wind speed of the typhoon is 15 meters per second at any distance from the center of the typhoon.
A)At a distance of 15 kilometers from the center of the typhoon, the wind speed is increasing.
B)At a distance of 15 kilometers from the center of the typhoon, the wind speed is positive.
C)The wind speed of the typhoon is 15 meters per second at any distance from the center of the typhoon.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
A function defined for all x has the following properties:
• f is increasing
• f is concave down
• f (4)= 2
•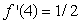 Is it possible that
Is it possible that 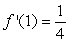 ?
?
• f is increasing
• f is concave down
• f (4)= 2
•
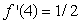 Is it possible that
Is it possible that 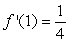 ?
?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Every day the Office of Undergraduate Admissions receives inquiries from eager high school students.They keep a running account of the number of inquiries received each day, along with the total number received until that point.Below is a table of weekly figures from about the end of August to about the end of October of a recent year. 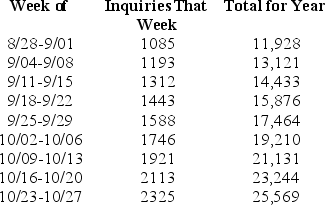 One of these columns can be interpreted as a rate of change.Which one is it?
One of these columns can be interpreted as a rate of change.Which one is it?
A)the first
B)the second
C)the third
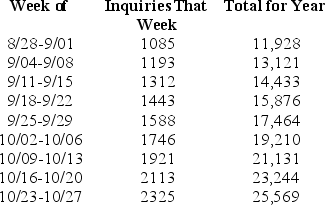 One of these columns can be interpreted as a rate of change.Which one is it?
One of these columns can be interpreted as a rate of change.Which one is it?A)the first
B)the second
C)the third

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Assume that f and g are differentiable functions defined on all of the real line.Is it possible that f '(x)> g'(x)for all x and f(x)< g(x)for all x?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
Given the function 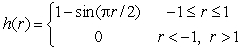 .Is
.Is 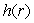 differentiable at r = -1?
differentiable at r = -1?
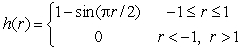 .Is
.Is 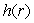 differentiable at r = -1?
differentiable at r = -1?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Assume that f and g are differentiable functions defined on all of the real line.If f'(x)= g'(x)for all x and if

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
A golf ball thrown directly upwards from the surface of the moon with an initial velocity of 17.00 meters per second and will attain a height of 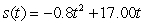 meters in t seconds.Find a formula for the velocity of the golf ball at time t.
meters in t seconds.Find a formula for the velocity of the golf ball at time t.
A)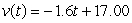 meters/sec
meters/sec
B)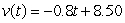
 meters/sec
meters/sec
C)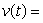 -1.36 meters/sec
-1.36 meters/sec
D)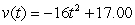 meters/sec
meters/sec
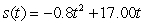 meters in t seconds.Find a formula for the velocity of the golf ball at time t.
meters in t seconds.Find a formula for the velocity of the golf ball at time t.A)
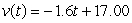 meters/sec
meters/secB)
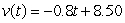
 meters/sec
meters/secC)
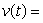 -1.36 meters/sec
-1.36 meters/secD)
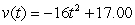 meters/sec
meters/sec
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
A golf ball thrown directly upwards from the surface of the moon with an initial velocity of 14.00 meters per second and will attain a height of 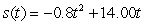 meters in t seconds.What is the acceleration of the golf ball at time t?
meters in t seconds.What is the acceleration of the golf ball at time t?
A)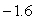 meters/sec/sec
meters/sec/sec
B)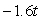 meters/sec2
meters/sec2
C)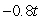 meters/sec/sec
meters/sec/sec
D)14.00 meters/sec2
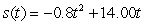 meters in t seconds.What is the acceleration of the golf ball at time t?
meters in t seconds.What is the acceleration of the golf ball at time t?A)
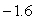 meters/sec/sec
meters/sec/secB)
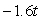 meters/sec2
meters/sec2C)
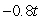 meters/sec/sec
meters/sec/secD)14.00 meters/sec2

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
Suppose a function is given by a table of values as follows:
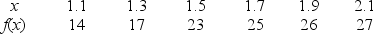 Give your best estimate of
Give your best estimate of 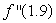 .
.
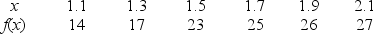 Give your best estimate of
Give your best estimate of 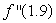 .
.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
Let S(t)represent the number of students enrolled in school in the year t.If the number of students enrolling is increasing faster and faster, then is S '(t)positive, negative, or 0?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
Assume that f and g are differentiable functions defined on all of the real line.If f ' > 0 everywhere and f > 0 everywhere then must 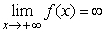 ?
?
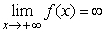 ?
?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
A company graphs C'(t), the derivative of the number of pints of ice cream sold over the past ten years.At approximately what year was C ''(t)greatest? 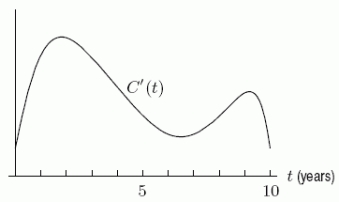


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
A golf ball thrown directly upwards from the surface of the moon with an initial velocity of 20 meters per second and will attain a height of 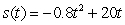 meters in t seconds.On Earth, its height would be given by
meters in t seconds.On Earth, its height would be given by 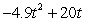 .Compare the velocity and acceleration of the golf ball on the moon after two seconds with its velocity and acceleration on Earth after two seconds.
.Compare the velocity and acceleration of the golf ball on the moon after two seconds with its velocity and acceleration on Earth after two seconds.
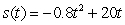 meters in t seconds.On Earth, its height would be given by
meters in t seconds.On Earth, its height would be given by 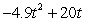 .Compare the velocity and acceleration of the golf ball on the moon after two seconds with its velocity and acceleration on Earth after two seconds.
.Compare the velocity and acceleration of the golf ball on the moon after two seconds with its velocity and acceleration on Earth after two seconds.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
Describe two ways that a continuous function can fail to have a derivative at a point, x = a.Illustrate your description with graphs.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
A husband and wife purchase life insurance policies.Over the next 40 years, one policy pays out when the husband dies, and the other pays out when both husband and wife die.Their life expectancy is 20 years, and the probability that both die before year t is given by the function 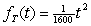 .How fast is the probability that both are dead increasing in 25 years?
.How fast is the probability that both are dead increasing in 25 years?
A)0.0313
B)0.3906
C)0.0500
D)50.0006
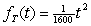 .How fast is the probability that both are dead increasing in 25 years?
.How fast is the probability that both are dead increasing in 25 years?A)0.0313
B)0.3906
C)0.0500
D)50.0006

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
Is the graph of 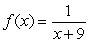 continuous at x = -9?
continuous at x = -9?
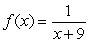 continuous at x = -9?
continuous at x = -9?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
The cost of mining a ton of coal is rising faster every year.Suppose C(t)is the cost of mining a ton of coal at time t.Must C ''(t)be concave up?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
If the Figure 1 is 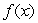 , could Figure 2 be
, could Figure 2 be 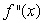 ?
? 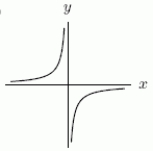
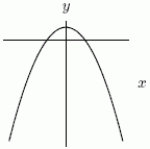 Figure 1 Figure 2
Figure 1 Figure 2
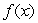 , could Figure 2 be
, could Figure 2 be 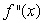 ?
? 
 Figure 1 Figure 2
Figure 1 Figure 2
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
Assume that f is a differentiable function defined on all of the real line.Is it possible that f > 0 everywhere, f ' > 0 everywhere, and f ' < 0 everywhere?

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
A golf ball thrown directly upwards from the surface of the moon with an initial velocity of 20 meters per second and will attain a height of 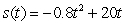 meters in t seconds.How fast is the golf ball going at its high point?
meters in t seconds.How fast is the golf ball going at its high point?
A)0 meters/sec
B)-0.8 meters/sec
C)20 meters/sec
D)-20 meters/sec
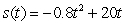 meters in t seconds.How fast is the golf ball going at its high point?
meters in t seconds.How fast is the golf ball going at its high point?A)0 meters/sec
B)-0.8 meters/sec
C)20 meters/sec
D)-20 meters/sec

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
Sketch a graph y = f(x)that is continuous everywhere on -6 < x < 6 but not differentiable at x = -3 or x = 3.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
Is the graph of 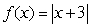 continuous at x = -3?
continuous at x = -3?
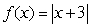 continuous at x = -3?
continuous at x = -3?
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
Sketch a graph of a continuous function f(x)with the following properties:
• f'(x)< 0 for x < 4
• f'(x)> 0 for x > 4
• f'(4)is undefined
• f'(x)< 0 for x < 4
• f'(x)> 0 for x > 4
• f'(4)is undefined

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


