Exam 2: Key Concept: the Derivative
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
A runner planned her strategy for running a half marathon, a distance of 13.1 miles.She planned to run negative splits, faster speeds as time passed during the race.In the actual race, she ran the first 6 miles in 48 minutes, the second 4 miles in 28 minutes and the last 3.1 miles in 18 minutes.What was her average velocity over the first 6 miles? What was her average velocity over the entire race? Did she run negative splits?
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
A function defined for all x has the following properties:
• f is increasing
• f is concave down
• f (4)= 2
•
Is it possible that
?
Free
(True/False)
4.9/5  (34)
(34)
Correct Answer:
False
The data in the table report the average improvement in scores of six college freshmen who took a writing assessment before and again after they had x hours of tutoring by a tutor trained in a new method of instruction.When f(x)>0 the group showed improvement on average.
x 2 3.5 5 6.5 8 9.5 11 f(x) -2 -1 0 3 7 9 10
a)Find the average change in score from 6.5 to 9.5 hours of tutoring.
b)Estimate the instantaneous rate of change at 8 hours.
c)Approximate the equation of the tangent line at x = 8 hours.
d)Use the tangent line to estimate f(8.5).
Free
(Essay)
4.8/5  (39)
(39)
Correct Answer:
a)2.00 points,
b)2.00 points, but answers may vary;
c)
;
d) 8 points
Let t(h)be the temperature in degrees Celsius at a height h (in meters)above the surface of the earth.What does t '(1200)mean in practical terms?
(Multiple Choice)
4.8/5  (31)
(31)
The cost in dollars to produce q bottles of a prescription skin treatment is given by the function
.The manufacturing process is difficult and costly when large quantities are produced.The marginal cost of producing one additional bottle when q bottles have been produced is the derivative
.
a)Find the marginal cost function.
b)Compute C(50)and explain what the number means in terms of cost and production.
c)Compute C'(50)and explain what the number means in terms of cost and production.
(Essay)
4.8/5  (34)
(34)
he graph below shows the velocity of a bug traveling along a straight line on the classroom floor. 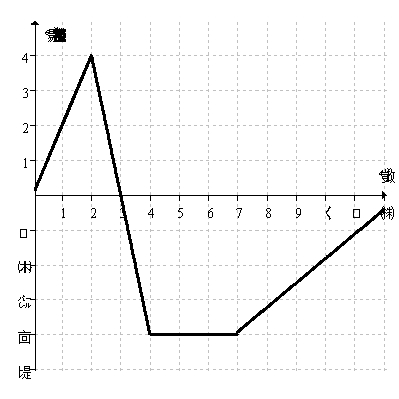 Graph the bug's speed at time, t.How does it differ from the bug's velocity?
Graph the bug's speed at time, t.How does it differ from the bug's velocity?
(Essay)
4.9/5  (34)
(34)
Alone in your dim, unheated room you light one candle rather than curse the darkness.Disgusted by the mess, you walk directly away from the candle.The temperature (in )and illumination (in % of one candle power)decrease as your distance (in feet)from the candle increases.The table below shows this information. distance(feet) Temp. illumination (\%) 0 55 100 1 54.5 85 2 53.5 75 3 52 67 4 50 60 5 47 56 6 43.5 53 You can still read your watch when the illumination is about 55%, so somewhere between 5 and 6 feet.Can you read your watch at 5.5 feet?
(Multiple Choice)
5.0/5  (42)
(42)
A golf ball thrown directly upwards from the surface of the moon with an initial velocity of 20 meters per second and will attain a height of
meters in t seconds.On Earth, its height would be given by
.Compare the velocity and acceleration of the golf ball on the moon after two seconds with its velocity and acceleration on Earth after two seconds.
(Essay)
4.9/5  (28)
(28)
Alone in your dim, unheated room you light one candle rather than curse the darkness.Disgusted by the mess, you walk directly away from the candle.The temperature (in )and illumination (in % of one candle power)decrease as your distance (in feet)from the candle increases.The table below shows this information.
distance(feet) Temp. () illuminatiou (\%) 0 55 100 1 54.5 85 2 53.5 75 3 52 67 4 50 60 5 47 56 6 43.5 53 Does the following graph show temperature or illumination as a function of distance? 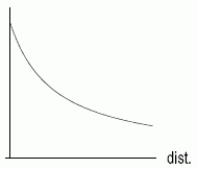
(Short Answer)
4.7/5  (42)
(42)
Consider the function y = f(x)graphed below.At the point x = -3, is
positive, negative, 0, or undefined?Note: f(x)is defined for -5 < x < 6, except x = 2. 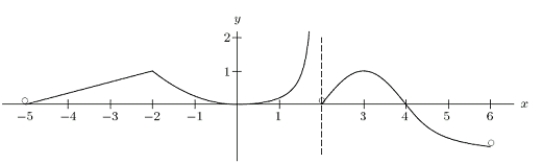
(Short Answer)
4.8/5  (41)
(41)
The height of an object in feet above the ground is given in the following table,
.Make a graph of f(t) .On your graph , what does the average velocity over a the interval
represent? t (sec) 0 1 2 3 4 5 6 y (feet) 10 45 70 85 90 85 70
(Multiple Choice)
4.9/5  (36)
(36)
Esther is a swimmer who prides herself in having a smooth backstroke.Let s(t)be her position in an Olympic size (50-meter)pool, as a function of time (s(t)is measured in meters, t is seconds).Below we list some values of s(t)for a recent swim.Find Esther's average speed over the entire swim in meters per second.Round to 2 decimal places.
t 0 3.0 8.6 14.64 21.35 28.06 32.33 39.04 46.36 54.9 61 s(t) 0 10 20 30 40 50 40 30 20 10 0
(Short Answer)
4.9/5  (31)
(31)
What is the equation of the tangent line to the graph of
at the point (2, 8)?
(Multiple Choice)
4.9/5  (33)
(33)
Sketch a graph y = f(x)that is continuous everywhere on -6 < x < 6 but not differentiable at x = -3 or x = 3.
(Essay)
4.9/5  (30)
(30)
For any number r, let m(r)be the slope of the graph of the function
at the point x = r.Estimate m(4)to 2 decimal places.
(Short Answer)
4.9/5  (44)
(44)
Use the definition of the derivative function to find a formula for the slope of the graph of
.
(Essay)
4.9/5  (22)
(22)
The graph below gives the position of a spider moving along a straight line on the forest floor for 10 seconds.On the same axes, sketch a graph of the spider's velocity over the 10 seconds.Then write a description of the spider's movement for the 10 second period. 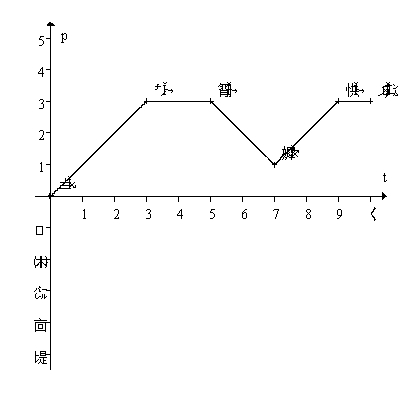
(Essay)
4.8/5  (40)
(40)
Let t(h)be the temperature in degrees Celsius at a height of h meters above the surface of the earth.What does h such that t(h)= 8 mean in practical terms?
(Multiple Choice)
4.9/5  (36)
(36)
Showing 1 - 20 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)