Deck 20: The Curl and Stokes Theorem
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/85
Play
Full screen (f)
Deck 20: The Curl and Stokes Theorem
1
True or false? If for all x, y, z and if S is a surface enclosing a volume V, then
A)Not possible to decide
B)True
C)False
A)Not possible to decide
B)True
C)False
False
2
Let be a smooth vector field.The flux of out of a small sphere of radius r centered at the point (1, , 2 )is 12 r3. Find at (1, , 2 )and use the result to estimate the flux of out of the small cube of side 0.025 centered around the point (1, , 2 ).
A)0.000141
B)0.005625
C)0.000125
D)0.00625
E)0.25
A)0.000141
B)0.005625
C)0.000125
D)0.00625
E)0.25
0.000141
3
Use the Divergence Theorem to find the flux of the vector field 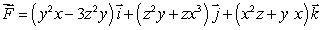 through the sphere x2 + y2 + z2 =
through the sphere x2 + y2 + z2 = 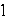 .
.
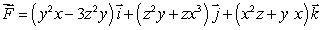 through the sphere x2 + y2 + z2 =
through the sphere x2 + y2 + z2 = 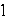 .
.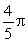
4
An oceanographic vessel suspends a paraboloid-shaped net below the ocean at depth of feet, held open at the top by a circular metal ring of radius feet, with bottom feet below the ring and just touching the ocean floor.Set up coordinates with the origin at the point where the net touches the ocean floor and with z measured upward. 
A)
B)
C)
D)
E)

A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
5
Let 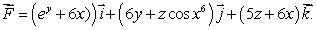 Calculate div
Calculate div 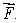
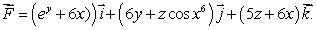 Calculate div
Calculate div 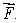

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
6
An oceanographic vessel suspends a paraboloid-shaped net below the ocean at depth of 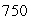 feet, held open at the top by a circular metal ring of radius
feet, held open at the top by a circular metal ring of radius 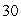 feet, with bottom
feet, with bottom 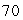 feet below the ring and just touching the ocean floor.Set up coordinates with the origin at the point where the net touches the ocean floor and with z measured upward.
feet below the ring and just touching the ocean floor.Set up coordinates with the origin at the point where the net touches the ocean floor and with z measured upward.

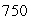 feet, held open at the top by a circular metal ring of radius
feet, held open at the top by a circular metal ring of radius 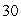 feet, with bottom
feet, with bottom 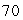 feet below the ring and just touching the ocean floor.Set up coordinates with the origin at the point where the net touches the ocean floor and with z measured upward.
feet below the ring and just touching the ocean floor.Set up coordinates with the origin at the point where the net touches the ocean floor and with z measured upward.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
7
Let 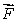 be a smooth velocity vector field describing the flow of a fluid.Suppose that
be a smooth velocity vector field describing the flow of a fluid.Suppose that 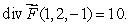 Will there be an inflow or outflow of fluid at the point (1, 2,-1)?
Will there be an inflow or outflow of fluid at the point (1, 2,-1)?
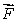 be a smooth velocity vector field describing the flow of a fluid.Suppose that
be a smooth velocity vector field describing the flow of a fluid.Suppose that 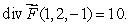 Will there be an inflow or outflow of fluid at the point (1, 2,-1)?
Will there be an inflow or outflow of fluid at the point (1, 2,-1)?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
8
Let 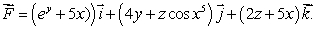 Calculate the flux
Calculate the flux 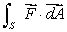 , where S is the sphere (x-2)2 + (y-3)2 + z2 =
, where S is the sphere (x-2)2 + (y-3)2 + z2 = 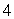 oriented inward.
oriented inward.
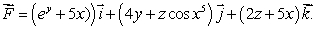 Calculate the flux
Calculate the flux 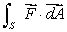 , where S is the sphere (x-2)2 + (y-3)2 + z2 =
, where S is the sphere (x-2)2 + (y-3)2 + z2 = 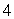 oriented inward.
oriented inward.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
9
If find
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the flux integral 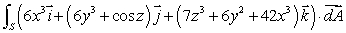 , where S is the surface of the cylinder x2 + y2 = 1 bounded by the planes z = -1, z = 1 (including the ends of the cylinder).
, where S is the surface of the cylinder x2 + y2 = 1 bounded by the planes z = -1, z = 1 (including the ends of the cylinder).
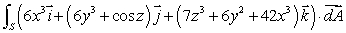 , where S is the surface of the cylinder x2 + y2 = 1 bounded by the planes z = -1, z = 1 (including the ends of the cylinder).
, where S is the surface of the cylinder x2 + y2 = 1 bounded by the planes z = -1, z = 1 (including the ends of the cylinder).
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the two-dimensional fluid flow given by 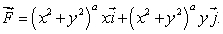 where a is a constant.
where a is a constant.
(We allow a to be negative, so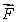 may or may not be defined at (0, 0).)
may or may not be defined at (0, 0).)
(a)Is the fluid flowing away from the origin, toward it, or neither?
(b)Calculate the divergence of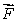 .Simplify your answer.
.Simplify your answer.
(c)For what values of a is div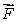 positive? Zero? Negative?
positive? Zero? Negative?
(d)What does your answer to (c)mean in terms of flow? How does this fit in with your answer to (a)?
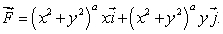 where a is a constant.
where a is a constant.(We allow a to be negative, so
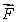 may or may not be defined at (0, 0).)
may or may not be defined at (0, 0).)(a)Is the fluid flowing away from the origin, toward it, or neither?
(b)Calculate the divergence of
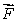 .Simplify your answer.
.Simplify your answer.(c)For what values of a is div
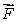 positive? Zero? Negative?
positive? Zero? Negative?(d)What does your answer to (c)mean in terms of flow? How does this fit in with your answer to (a)?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
12
Let 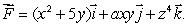 Given that
Given that 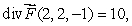 find the value of a.
find the value of a.
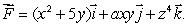 Given that
Given that 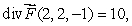 find the value of a.
find the value of a.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
13
(a)Is 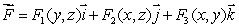 a divergence free vector field?
a divergence free vector field?
(b)Do all divergence free vector fields have the form of the vector field in (a)?
(c)If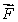 has the form given in (a)can we conclude that
has the form given in (a)can we conclude that 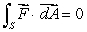 for any closed surface S?
for any closed surface S?
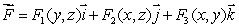 a divergence free vector field?
a divergence free vector field?(b)Do all divergence free vector fields have the form of the vector field in (a)?
(c)If
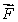 has the form given in (a)can we conclude that
has the form given in (a)can we conclude that 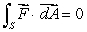 for any closed surface S?
for any closed surface S?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
14
Let , where p is a positive constant.Is there a value of p such that is a divergence free vector field?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
15
Let 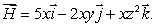 What is
What is 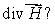
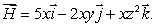 What is
What is 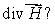

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose 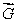 is a vector field with the property that
is a vector field with the property that 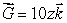 at every point of the surface
at every point of the surface 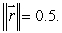 If
If 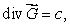 where c is a constant, find c.
where c is a constant, find c.
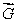 is a vector field with the property that
is a vector field with the property that 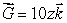 at every point of the surface
at every point of the surface 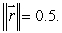 If
If 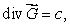 where c is a constant, find c.
where c is a constant, find c.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
17
Let 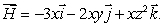 ,
,
What is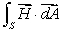 , where S is the cube with corners at (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1,0,1), (0,1,1), and (1, 1, 1)?
, where S is the cube with corners at (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1,0,1), (0,1,1), and (1, 1, 1)?
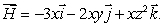 ,
,What is
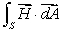 , where S is the cube with corners at (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1,0,1), (0,1,1), and (1, 1, 1)?
, where S is the cube with corners at (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1,0,1), (0,1,1), and (1, 1, 1)?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
18
Let be a constant vector and f(x, y, z)be a smooth function.Which statement is true?
A)If is a divergence free vector field then f is parallel to
B)If is not a divergence free vector field then f is perpendicular to
C)If is a divergence free vector field then f is perpendicular to
D)If is not a divergence free vector field then f is parallel to
E)If is a divergence free vector field then f is constant.
A)If is a divergence free vector field then f is parallel to
B)If is not a divergence free vector field then f is perpendicular to
C)If is a divergence free vector field then f is perpendicular to
D)If is not a divergence free vector field then f is parallel to
E)If is a divergence free vector field then f is constant.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
19
State the Divergence Theorem.
A)If W is a solid region whose boundary S is a piecewise smooth surface, then
B)If W is a solid region whose boundary S is a smooth surface oriented outward, then
C)If W is a solid region whose boundary S is a piecewise smooth surface oriented outward, and if is a smooth vector field on an open region containing W and S, then
D)If W is a solid region whose boundary S is a piecewise smooth surface oriented outward, then
E)If S is a solid region whose boundary W is a piecewise smooth surface oriented outward, then
A)If W is a solid region whose boundary S is a piecewise smooth surface, then
B)If W is a solid region whose boundary S is a smooth surface oriented outward, then
C)If W is a solid region whose boundary S is a piecewise smooth surface oriented outward, and if is a smooth vector field on an open region containing W and S, then
D)If W is a solid region whose boundary S is a piecewise smooth surface oriented outward, then
E)If S is a solid region whose boundary W is a piecewise smooth surface oriented outward, then

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
20
Let 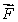 be a smooth velocity vector field describing the flow of a fluid.Suppose that
be a smooth velocity vector field describing the flow of a fluid.Suppose that 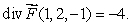 Estimate the value of
Estimate the value of 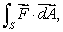 where S is a sphere of radius 0.25 centered at (1, 2,-1)oriented outward.Give your answer to 4 decimal places.
where S is a sphere of radius 0.25 centered at (1, 2,-1)oriented outward.Give your answer to 4 decimal places.
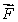 be a smooth velocity vector field describing the flow of a fluid.Suppose that
be a smooth velocity vector field describing the flow of a fluid.Suppose that 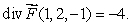 Estimate the value of
Estimate the value of 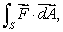 where S is a sphere of radius 0.25 centered at (1, 2,-1)oriented outward.Give your answer to 4 decimal places.
where S is a sphere of radius 0.25 centered at (1, 2,-1)oriented outward.Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
21
Let 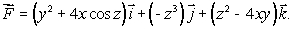 Find the curl of
Find the curl of 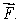
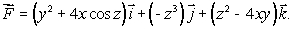 Find the curl of
Find the curl of 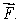

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
22
Find 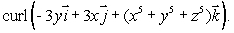
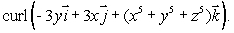

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
23
Let 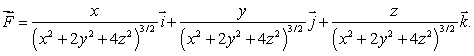 Use the Divergence Theorem to calculate
Use the Divergence Theorem to calculate 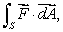 where S is the sphere of radius
where S is the sphere of radius 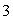 a centered at the point (
a centered at the point ( 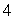 a, 0, 0).
a, 0, 0).
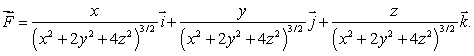 Use the Divergence Theorem to calculate
Use the Divergence Theorem to calculate 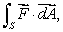 where S is the sphere of radius
where S is the sphere of radius 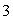 a centered at the point (
a centered at the point ( 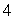 a, 0, 0).
a, 0, 0).
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
24
Let 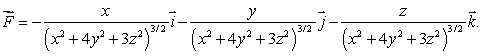 Is
Is 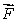 a divergence free vector field?
a divergence free vector field?
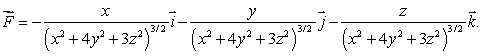 Is
Is 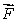 a divergence free vector field?
a divergence free vector field?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
25
Let 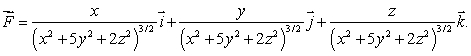 Let S1 be the sphere of radius
Let S1 be the sphere of radius 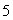 centered at the origin, oriented outward and let S2 be the sphere of radius
centered at the origin, oriented outward and let S2 be the sphere of radius 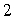 centered at the origin, also oriented outward.
centered at the origin, also oriented outward.
Do you expect the value of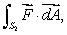 to be larger, smaller or the same as
to be larger, smaller or the same as 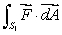 ?
?
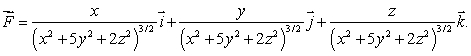 Let S1 be the sphere of radius
Let S1 be the sphere of radius 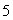 centered at the origin, oriented outward and let S2 be the sphere of radius
centered at the origin, oriented outward and let S2 be the sphere of radius 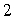 centered at the origin, also oriented outward.
centered at the origin, also oriented outward.Do you expect the value of
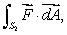 to be larger, smaller or the same as
to be larger, smaller or the same as 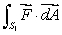 ?
?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
26
Use the Divergence Theorem to find the flux of the vector field through the cube 0 x 1, 0 y 1, 0 z 1.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
27
Let 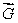 be a smooth vector field with curl
be a smooth vector field with curl 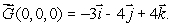 Estimate the circulation around a circle of radius 0.01 in the yz plane, oriented counterclockwise when viewed from the positive x-axis.
Estimate the circulation around a circle of radius 0.01 in the yz plane, oriented counterclockwise when viewed from the positive x-axis.
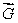 be a smooth vector field with curl
be a smooth vector field with curl 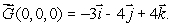 Estimate the circulation around a circle of radius 0.01 in the yz plane, oriented counterclockwise when viewed from the positive x-axis.
Estimate the circulation around a circle of radius 0.01 in the yz plane, oriented counterclockwise when viewed from the positive x-axis.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
28
Suppose that is a vector field defined everywhere with constant negative divergence C.Decide if the following statement is true.
There is surface S for which
There is surface S for which

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
29
Let 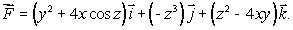 Find the divergence of
Find the divergence of 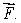
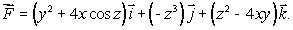 Find the divergence of
Find the divergence of 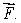

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
30
Calculate where
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
31
If everywhere and S is a smooth surface (oriented outward)enclosing a volume W of size V find .
A)
B)
C)
D)
E)0
A)
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
32
Below is a picture of the vector field 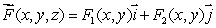 from above.
from above. 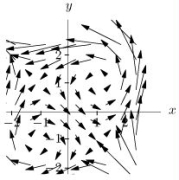 Match the value of curl
Match the value of curl 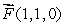 with one of the following values:
with one of the following values: 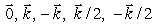
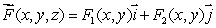 from above.
from above.  Match the value of curl
Match the value of curl 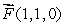 with one of the following values:
with one of the following values: 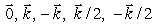

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
The figure below shows a vector field of the form

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
33
How is curl 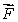 defined? Select all that apply.
defined? Select all that apply.
A)curl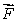 is a vector in the direction
is a vector in the direction
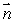 for which
for which
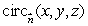 is the greatest that has magnitude equal to the circulation density of
is the greatest that has magnitude equal to the circulation density of
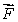 around that direction.
around that direction.
B)If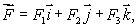 then
then
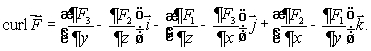
C)curl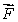 is a vector in the direction
is a vector in the direction
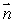 for which the circulation is greatest and has magnitude equal to the circulation of
for which the circulation is greatest and has magnitude equal to the circulation of
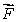 around that direction.
around that direction.
D)If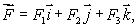 then
then
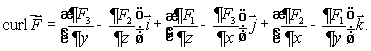
E)If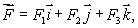 then
then
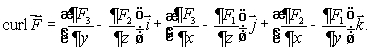
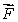 defined? Select all that apply.
defined? Select all that apply.A)curl
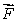 is a vector in the direction
is a vector in the direction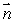 for which
for which is the greatest that has magnitude equal to the circulation density of
is the greatest that has magnitude equal to the circulation density of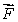 around that direction.
around that direction.B)If
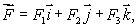 then
then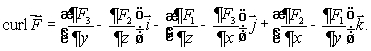
C)curl
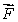 is a vector in the direction
is a vector in the direction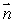 for which the circulation is greatest and has magnitude equal to the circulation of
for which the circulation is greatest and has magnitude equal to the circulation of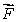 around that direction.
around that direction.D)If
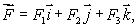 then
then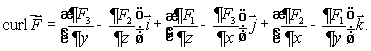
E)If
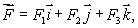 then
then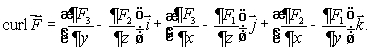

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
34
Suppose 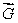 is a vector field with the property that
is a vector field with the property that 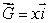 at every point of the surface
at every point of the surface 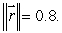 If
If 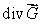 is not a constant, estimate the value of
is not a constant, estimate the value of 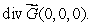
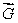 is a vector field with the property that
is a vector field with the property that 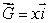 at every point of the surface
at every point of the surface 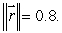 If
If 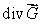 is not a constant, estimate the value of
is not a constant, estimate the value of 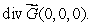

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
35
What is meant by curl where is a vector field? Is curl a vector or a scalar?
A)curl is a scalar which tells you how a vector field is rotating.Its direction gives the axis of rotation; its magnitude gives the strength of rotation about the axis.
B)curl is a vector which tells you how a scalar field is rotating.Its direction gives the axis of rotation; its magnitude gives the strength of rotation about the axis.
C)curl is a vector which tells you how a vector field is rotating.Its direction gives the axis of rotation; its magnitude gives the strength of rotation about the axis.
D)curl is a vector which tells you how a vector field is rotating.Its magnitude gives the axis of rotation; its direction gives the strength of rotation about the axis.
E)curl is a scalar which tells you how a scalar field is rotating.Its magnitude gives the strength of rotation about the axis.
A)curl is a scalar which tells you how a vector field is rotating.Its direction gives the axis of rotation; its magnitude gives the strength of rotation about the axis.
B)curl is a vector which tells you how a scalar field is rotating.Its direction gives the axis of rotation; its magnitude gives the strength of rotation about the axis.
C)curl is a vector which tells you how a vector field is rotating.Its direction gives the axis of rotation; its magnitude gives the strength of rotation about the axis.
D)curl is a vector which tells you how a vector field is rotating.Its magnitude gives the axis of rotation; its direction gives the strength of rotation about the axis.
E)curl is a scalar which tells you how a scalar field is rotating.Its magnitude gives the strength of rotation about the axis.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
36
Let
A)The answer in (a)is bigger than (b).
B)The answer in (a)is smaller than (b).
C)They are the same.
A)The answer in (a)is bigger than (b).
B)The answer in (a)is smaller than (b).
C)They are the same.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
37
Suppose that 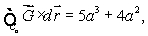 where Ca is the circle
where Ca is the circle 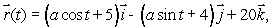 for any a > 0.
for any a > 0.
Does knowing this tell you anything about curl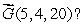 Is so, what? If not, why not?
Is so, what? If not, why not?
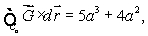 where Ca is the circle
where Ca is the circle 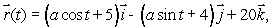 for any a > 0.
for any a > 0.Does knowing this tell you anything about curl
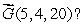 Is so, what? If not, why not?
Is so, what? If not, why not?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
38
Let 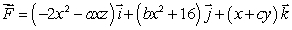 be a smooth vector field with
be a smooth vector field with 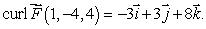 Determine the values of a, b and c.
Determine the values of a, b and c.
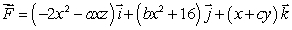 be a smooth vector field with
be a smooth vector field with 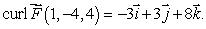 Determine the values of a, b and c.
Determine the values of a, b and c.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose that 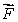 is a vector field defined everywhere with constant negative divergence C.Decide if the following statement is true and explain your answer.
is a vector field defined everywhere with constant negative divergence C.Decide if the following statement is true and explain your answer. 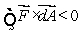 for every
for every 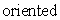 surface S.
surface S.
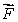 is a vector field defined everywhere with constant negative divergence C.Decide if the following statement is true and explain your answer.
is a vector field defined everywhere with constant negative divergence C.Decide if the following statement is true and explain your answer. 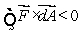 for every
for every 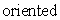 surface S.
surface S.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
40
Show that the vector field is a divergence free vector field.
Use this result to calculate where S is the open surface which is the graph of with f(x, y) 0.
Use this result to calculate where S is the open surface which is the graph of with f(x, y) 0.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose a vector field 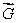 is always perpendicular to the normal vector at each point of a surface S.What is the value of
is always perpendicular to the normal vector at each point of a surface S.What is the value of 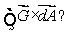
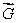 is always perpendicular to the normal vector at each point of a surface S.What is the value of
is always perpendicular to the normal vector at each point of a surface S.What is the value of 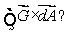

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
42
Let 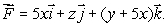 Use Stokes' Theorem to find
Use Stokes' Theorem to find 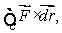 where C is a circle in the xz-plane of radius
where C is a circle in the xz-plane of radius 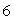 , centered at
, centered at 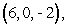 oriented
oriented 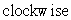 when viewed from the positive y-axis.
when viewed from the positive y-axis.
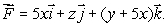 Use Stokes' Theorem to find
Use Stokes' Theorem to find 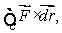 where C is a circle in the xz-plane of radius
where C is a circle in the xz-plane of radius 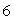 , centered at
, centered at 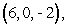 oriented
oriented 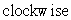 when viewed from the positive y-axis.
when viewed from the positive y-axis.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
43
Let 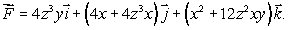 (a)Evaluate the line integral
(a)Evaluate the line integral 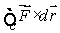 , where C is the circle
, where C is the circle 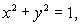 on the xy-plane, oriented in a counter-clockwise direction when viewed from above.
on the xy-plane, oriented in a counter-clockwise direction when viewed from above.
(b)Without any computation, explain why the answer in part (a)is also equal to the flux integral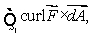 where S1 is lower hemisphere
where S1 is lower hemisphere 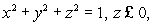 oriented inward.
oriented inward.
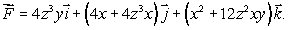 (a)Evaluate the line integral
(a)Evaluate the line integral 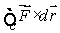 , where C is the circle
, where C is the circle 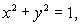 on the xy-plane, oriented in a counter-clockwise direction when viewed from above.
on the xy-plane, oriented in a counter-clockwise direction when viewed from above.(b)Without any computation, explain why the answer in part (a)is also equal to the flux integral
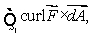 where S1 is lower hemisphere
where S1 is lower hemisphere 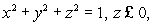 oriented inward.
oriented inward.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose that curl is not zero.True or false? If curl is parallel to the -axis for all x, y, and z and if C is a circle in the xy-plane, then the circulation of around C is zero.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
45
Given 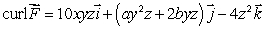 , find the values of the constants a and b, without knowing the expression of
, find the values of the constants a and b, without knowing the expression of 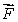 .
.
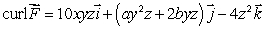 , find the values of the constants a and b, without knowing the expression of
, find the values of the constants a and b, without knowing the expression of 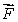 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
46
Given that 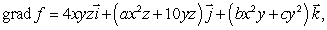 use the curl test to find the values of the constants a, b and c.
use the curl test to find the values of the constants a, b and c.
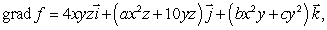 use the curl test to find the values of the constants a, b and c.
use the curl test to find the values of the constants a, b and c.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
47
Use the curl test to determine whether the following vector field is a gradient field.
A)Only at the origin
B)No
C)Yes
A)Only at the origin
B)No
C)Yes

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
48
Let (a)Use Stokes' Theorem to find the circulation of around the circle of radius a, for 0 t 2 .
(b)Use this result to find the component of
(b)Use this result to find the component of

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
49
If then by Stokes' Theorem the line integral is equal to zero, where C is the curve y = x2, for 0 x 2.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose that the flux of a smooth vector field 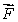 out of a sphere of radius r centered at the origin is
out of a sphere of radius r centered at the origin is 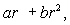 where a and b are constants.If
where a and b are constants.If 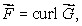 for a smooth vector field
for a smooth vector field 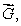 find the values of a and b.
find the values of a and b.
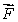 out of a sphere of radius r centered at the origin is
out of a sphere of radius r centered at the origin is 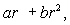 where a and b are constants.If
where a and b are constants.If 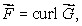 for a smooth vector field
for a smooth vector field 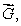 find the values of a and b.
find the values of a and b.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose that curl 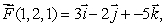 curl
curl 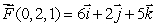 and curl
and curl 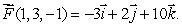 Estimate the following line integrals.
Estimate the following line integrals.
(a)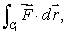 where C1 is given by
where C1 is given by 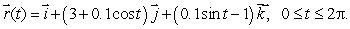 (b)
(b) 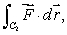 where C2 is given by
where C2 is given by 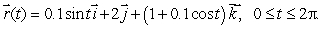 (c)
(c) 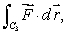 where C3 is given by
where C3 is given by 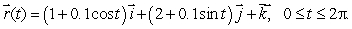
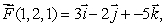 curl
curl 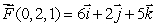 and curl
and curl 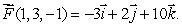 Estimate the following line integrals.
Estimate the following line integrals.(a)
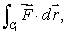 where C1 is given by
where C1 is given by 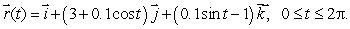 (b)
(b) 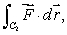 where C2 is given by
where C2 is given by 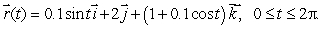 (c)
(c) 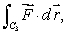 where C3 is given by
where C3 is given by 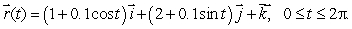

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
52
You want to build a windmill at the origin that maximizes the circulation of the wind.The wind vector field at any point (x, y, z)in your coordinate world is given by 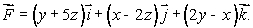
(a)In which direction should you face the windmill to get maximum use from the wind?
(b)What will be the strength of the circulation of the wind when you face it in this direction?
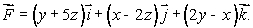
(a)In which direction should you face the windmill to get maximum use from the wind?
(b)What will be the strength of the circulation of the wind when you face it in this direction?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
53
Let
(a)By direct computation, find the circulation of around the circle of radius a, for 0 t 2 .
(b)Use this result to find the component of
(a)By direct computation, find the circulation of around the circle of radius a, for 0 t 2 .
(b)Use this result to find the component of

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
54
Let 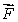 be a vector field such that
be a vector field such that 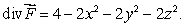 (a)Is
(a)Is 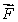 a curl field?
a curl field?
(b)Use spherical coordinates to evaluate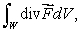 where W is the solid ball of radius R centered at the origin.
where W is the solid ball of radius R centered at the origin.
(c)Use the result of part (b)to find the radius of a sphere centered at the origin, such that the flux of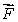 out of this sphere is zero.
out of this sphere is zero.
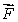 be a vector field such that
be a vector field such that 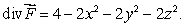 (a)Is
(a)Is 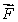 a curl field?
a curl field?(b)Use spherical coordinates to evaluate
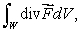 where W is the solid ball of radius R centered at the origin.
where W is the solid ball of radius R centered at the origin.(c)Use the result of part (b)to find the radius of a sphere centered at the origin, such that the flux of
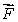 out of this sphere is zero.
out of this sphere is zero.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
55
State Stokes' Theorem.
A)If S is a smooth oriented surface with smooth, oriented boundary C, then
B)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, then
C)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, then
D)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, and if is a smooth vector field on an open region containing S and C, then
E)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, then
A)If S is a smooth oriented surface with smooth, oriented boundary C, then
B)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, then
C)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, then
D)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, and if is a smooth vector field on an open region containing S and C, then
E)If S is a smooth oriented surface with piecewise smooth, oriented boundary C, then

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
56
The trumpet surface, S, is given parametrically by 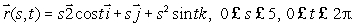
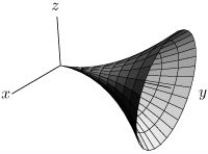 If S has outward pointing normal, use an appropriate line integral to calculate
If S has outward pointing normal, use an appropriate line integral to calculate 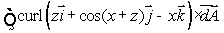
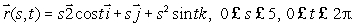
 If S has outward pointing normal, use an appropriate line integral to calculate
If S has outward pointing normal, use an appropriate line integral to calculate 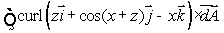

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
57
(a)The vector field 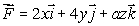 has the property that the flux of
has the property that the flux of 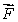 through any closed surface is 0.What is the value of the constant a?
through any closed surface is 0.What is the value of the constant a?
(b)The vector field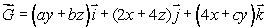 has the property that the circulation of
has the property that the circulation of 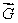 around any closed curve is 0.What are the values of the constants a, b and c?
around any closed curve is 0.What are the values of the constants a, b and c?
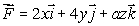 has the property that the flux of
has the property that the flux of 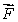 through any closed surface is 0.What is the value of the constant a?
through any closed surface is 0.What is the value of the constant a?(b)The vector field
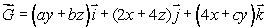 has the property that the circulation of
has the property that the circulation of 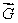 around any closed curve is 0.What are the values of the constants a, b and c?
around any closed curve is 0.What are the values of the constants a, b and c?
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
58
Let Let C be the circle of radius a parameterized by x = a cos t, y = 0, z = a sin t, 0 t 2 and let S be the disk in the xz-plane enclosed by C, oriented in the positive y-direction.
(a)Evaluate directly (b)Evaluate directly (c)Do these results contradict Stokes' Theorem?
(a)Evaluate directly (b)Evaluate directly (c)Do these results contradict Stokes' Theorem?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
59
Suppose that the flux of a smooth vector field 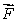 out of a sphere of radius r centered at the origin is ar3 + br4, where a and b are constants.Calculate
out of a sphere of radius r centered at the origin is ar3 + br4, where a and b are constants.Calculate 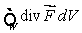 , where W is the solid
, where W is the solid 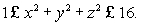
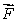 out of a sphere of radius r centered at the origin is ar3 + br4, where a and b are constants.Calculate
out of a sphere of radius r centered at the origin is ar3 + br4, where a and b are constants.Calculate 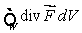 , where W is the solid
, where W is the solid 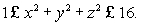

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
60
Let 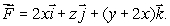 Use Stokes' Theorem to find
Use Stokes' Theorem to find 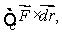 where C is a circle in the xy-plane of radius
where C is a circle in the xy-plane of radius 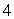 , centered at
, centered at 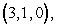 oriented counter-clockwise when viewed from above.
oriented counter-clockwise when viewed from above.
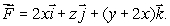 Use Stokes' Theorem to find
Use Stokes' Theorem to find 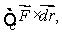 where C is a circle in the xy-plane of radius
where C is a circle in the xy-plane of radius 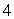 , centered at
, centered at 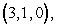 oriented counter-clockwise when viewed from above.
oriented counter-clockwise when viewed from above.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
61
Let P be a plane through the origin with equation 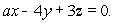 Let
Let 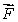 be a vector field with curl
be a vector field with curl 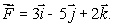 Suppose
Suppose 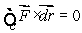 for any closed curve on the plane
for any closed curve on the plane 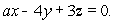 Using Stokes' Theorem, determine the value of a.
Using Stokes' Theorem, determine the value of a.
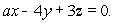 Let
Let 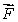 be a vector field with curl
be a vector field with curl 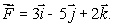 Suppose
Suppose 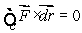 for any closed curve on the plane
for any closed curve on the plane 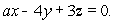 Using Stokes' Theorem, determine the value of a.
Using Stokes' Theorem, determine the value of a.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
62
Let be a smooth vector field with at every point in space and let S1 and S2 be spheres of radius r, oriented outward, centered at (0,0,0)and at (1,2,1), respectively.
.
.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
63
Let S be the closed surface which is the portion of the sphere with topped by the disk in the plane , oriented outward.Then the flux of through S is:
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
64
Let S be the surface of the upper part of the cylinder 4x2 + z2 = 1, z 0, between the planes y = -1, y = 1, with an upward-pointing normal.
(a)Evaluate the flux integral (b)Consider W, the solid region described by -1 y 1, 4x2 + z2 1, z 0.Evaluate Does this contradict the Divergence Theorem? Explain.
(a)Evaluate the flux integral (b)Consider W, the solid region described by -1 y 1, 4x2 + z2 1, z 0.Evaluate Does this contradict the Divergence Theorem? Explain.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
65
For the following integral, say whether Stokes' Theorem, the Divergence Theorem, or neither applies. where S is a triangular plane in space oriented upward.
A)Stokes' Theorem
B)Divergence Theorem.
C)Neither
A)Stokes' Theorem
B)Divergence Theorem.
C)Neither

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
66
Using either Stokes' theorem or the Divergence theorem (whichever is appropriate), evaluate 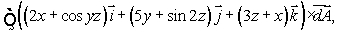 where S is the sphere of radius 2 oriented outward and centered at the point
where S is the sphere of radius 2 oriented outward and centered at the point 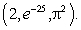
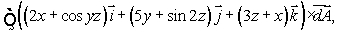 where S is the sphere of radius 2 oriented outward and centered at the point
where S is the sphere of radius 2 oriented outward and centered at the point 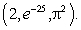

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
67
Let 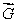 be a smooth vector field with
be a smooth vector field with 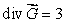 at every point in space.Find the exponent p in the following:
at every point in space.Find the exponent p in the following: 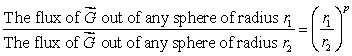
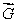 be a smooth vector field with
be a smooth vector field with 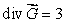 at every point in space.Find the exponent p in the following:
at every point in space.Find the exponent p in the following: 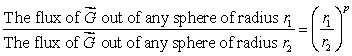

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
68
For the following integral, say whether Stokes' Theorem, the Divergence Theorem, or neither applies. where C is a closed loop in space.
A)Stokes' Theorem
B)Divergence Theorem.
C)Neither
A)Stokes' Theorem
B)Divergence Theorem.
C)Neither

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
69
On an exam, students are asked to find the line integral of over the curve C which is the boundary of the upper hemisphere oriented in a counter-clockwise direction when viewed from above.One student wrote: " By Stokes' Theorem where S is the hemisphere.Since by the Divergence Theorem where W is the solid hemisphere.Hence we have "
This answer is wrong.Which part of the student's argument is wrong? Select all that apply.
A)The student has been careless with the orientations of the curve and surface.
B)The student has to be careful with the orientations of the curve and surface.However, Stokes' Theorem has been applied correctly.
C)The student has used Divergence Theorem incorrectly.The upper hemisphere S does not include the bottom, hence it does not enclose any region in space, and we cannot apply the Divergence Theorem to this surface.
D)The student has to be careful with the orientations of the curve and surface.However, the Divergence Theorem has been applied correctly.
E)The student has the correct orientations of the curve and surface but the student has used Divergence Theorem for the hemisphere incorrectly.The upper hemisphere S does not include the bottom, hence it does not enclose any region in space, and we cannot apply the Divergence Theorem to this surface.
This answer is wrong.Which part of the student's argument is wrong? Select all that apply.
A)The student has been careless with the orientations of the curve and surface.
B)The student has to be careful with the orientations of the curve and surface.However, Stokes' Theorem has been applied correctly.
C)The student has used Divergence Theorem incorrectly.The upper hemisphere S does not include the bottom, hence it does not enclose any region in space, and we cannot apply the Divergence Theorem to this surface.
D)The student has to be careful with the orientations of the curve and surface.However, the Divergence Theorem has been applied correctly.
E)The student has the correct orientations of the curve and surface but the student has used Divergence Theorem for the hemisphere incorrectly.The upper hemisphere S does not include the bottom, hence it does not enclose any region in space, and we cannot apply the Divergence Theorem to this surface.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
70
Let S be the boundary surface of a solid region W with outward-pointing normal.Using an appropriate theorem, change the following flux integral into volume integral over W. 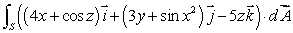
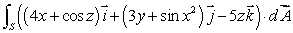

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
71
Suppose that 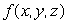 is defined and differentiable everywhere and satisfies the differential equation
is defined and differentiable everywhere and satisfies the differential equation 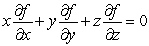 .Let
.Let 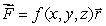 , where
, where 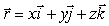 .Suppose that S is a closed surface and W is its interior.Find Q in the following equation:
.Suppose that S is a closed surface and W is its interior.Find Q in the following equation: 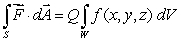 .
.
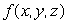 is defined and differentiable everywhere and satisfies the differential equation
is defined and differentiable everywhere and satisfies the differential equation 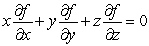 .Let
.Let 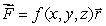 , where
, where 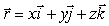 .Suppose that S is a closed surface and W is its interior.Find Q in the following equation:
.Suppose that S is a closed surface and W is its interior.Find Q in the following equation: 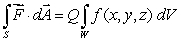 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
72
Let 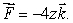
(a)Compute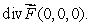 .
.
(b) By direct computation, find the flux of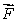 through a cube with edge length l, centered at the origin and edges parallel to the axes.
through a cube with edge length l, centered at the origin and edges parallel to the axes.
(c)Explain how your answers in parts (b)are related to that of part (a).
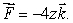
(a)Compute
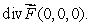 .
. (b) By direct computation, find the flux of
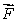 through a cube with edge length l, centered at the origin and edges parallel to the axes.
through a cube with edge length l, centered at the origin and edges parallel to the axes.(c)Explain how your answers in parts (b)are related to that of part (a).

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
73
Suppose 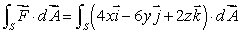 for any closed surface S in space with outward-pointing normal.What does this tell you about
for any closed surface S in space with outward-pointing normal.What does this tell you about 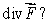
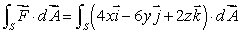 for any closed surface S in space with outward-pointing normal.What does this tell you about
for any closed surface S in space with outward-pointing normal.What does this tell you about 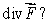

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
74
Using either Stokes' theorem or the Divergence theorem (whichever is appropriate), evaluate the following: 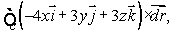 where C is a closed loop parameterized by
where C is a closed loop parameterized by 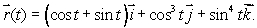
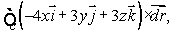 where C is a closed loop parameterized by
where C is a closed loop parameterized by 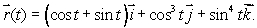

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
75
Let be a nonzero constant vector and let .Suppose S is the sphere of radius one centered at the origin.There are two (related)reasons why .Select them both.
A) because .
B) because .
C) because is parallel to the
element everywhere on S and so
is perpendicular to
on S.
D) because is a constant vector field.
E) because and
, where H is the upper unit hemisphere and L is the lower unit hemisphere.
A) because .
B) because .
C) because is parallel to the
element everywhere on S and so
is perpendicular to
on S.
D) because is a constant vector field.
E) because and
, where H is the upper unit hemisphere and L is the lower unit hemisphere.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
76
Suppose that is a smooth vector field, defined everywhere.
It is possible that , where S is a sphere of radius r centered at the origin.
It is possible that , where S is a sphere of radius r centered at the origin.

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
77
A physicist is asked to find the flux of a magnetic field through the curved surface of a right circular cone.The cone is of height 4 and has a circular base of radius 2.He says immediately that, by the Divergence Theorem, the answer is 16 .How did he know?

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
78
Let 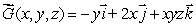 .Calculate curl
.Calculate curl 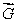 .
.
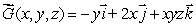 .Calculate curl
.Calculate curl 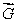 .
.
Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck
79
For the following integral, say whether Stokes' Theorem, the Divergence Theorem, or neither applies. where S is a triangular plane in space oriented
A)Stokes' Theorem
B)Divergence Theorem.
C)Neither
A)Stokes' Theorem
B)Divergence Theorem.
C)Neither

Unlock Deck
Unlock for access to all 85 flashcards in this deck.
Unlock Deck
k this deck


