Deck 19: Flux Integrals and Divergence
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/52
Play
Full screen (f)
Deck 19: Flux Integrals and Divergence
1
Let 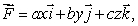 where a, b and c are constants.Suppose that the flux of
where a, b and c are constants.Suppose that the flux of 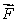 through a surface of area 3 lying in the plane y = 3, oriented in the positive y-direction, is 45.Find the flux of
through a surface of area 3 lying in the plane y = 3, oriented in the positive y-direction, is 45.Find the flux of 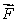 through a surface of area 4 lying in the plane y = 3, oriented in the negative y-direction.
through a surface of area 4 lying in the plane y = 3, oriented in the negative y-direction.
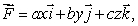 where a, b and c are constants.Suppose that the flux of
where a, b and c are constants.Suppose that the flux of 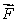 through a surface of area 3 lying in the plane y = 3, oriented in the positive y-direction, is 45.Find the flux of
through a surface of area 3 lying in the plane y = 3, oriented in the positive y-direction, is 45.Find the flux of 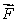 through a surface of area 4 lying in the plane y = 3, oriented in the negative y-direction.
through a surface of area 4 lying in the plane y = 3, oriented in the negative y-direction.-60
2
What is the flux of the vector field 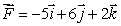 through a circle in the xy-plane of radius 2 oriented upward with center at the origin?
through a circle in the xy-plane of radius 2 oriented upward with center at the origin?
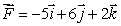 through a circle in the xy-plane of radius 2 oriented upward with center at the origin?
through a circle in the xy-plane of radius 2 oriented upward with center at the origin?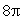
3
is a vector.
True
4
A circular disk, S, of radius 2 and centered on an axis, is perpendicular to the y-axis at y = -6 with normal in the direction of decreasing y. Consider the vector field .Is the flux integral positive, negative or zero?
A)Positive
B)Zero
C)Negative
A)Positive
B)Zero
C)Negative

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose S is a disk of radius 2 in the plane x + z = 0 centered at (0, 0, 0)oriented "upward".
Calculate the flux of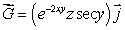 through S.
through S.
Calculate the flux of
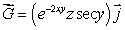 through S.
through S.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
6
Let 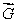 be the constant vector field
be the constant vector field 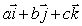 .
.
Find a condition on a, b and c such that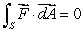 for any surface S lying on the plane -5x + 3y - 2z = 1.
for any surface S lying on the plane -5x + 3y - 2z = 1.
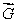 be the constant vector field
be the constant vector field  .
.Find a condition on a, b and c such that
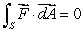 for any surface S lying on the plane -5x + 3y - 2z = 1.
for any surface S lying on the plane -5x + 3y - 2z = 1.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
7
Compute the flux integral of the vector field 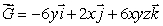 through the square
through the square 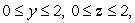 in the yz-plane, oriented so that the normal vector points in the direction of the x-axis.
in the yz-plane, oriented so that the normal vector points in the direction of the x-axis.
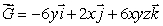 through the square
through the square 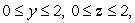 in the yz-plane, oriented so that the normal vector points in the direction of the x-axis.
in the yz-plane, oriented so that the normal vector points in the direction of the x-axis.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
8
Calculate the flux of 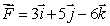 through a surface of area 3 lying in the plane 2x + 5y + 5z = 10, oriented away from the origin.
through a surface of area 3 lying in the plane 2x + 5y + 5z = 10, oriented away from the origin.
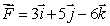 through a surface of area 3 lying in the plane 2x + 5y + 5z = 10, oriented away from the origin.
through a surface of area 3 lying in the plane 2x + 5y + 5z = 10, oriented away from the origin.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
9
Let S be the sphere of radius 3 centered at the origin, oriented outward.
Suppose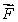 is normal to
is normal to 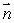 at every point of S.Find the flux of
at every point of S.Find the flux of 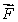 out of S.
out of S.
Suppose
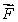 is normal to
is normal to 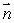 at every point of S.Find the flux of
at every point of S.Find the flux of 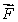 out of S.
out of S.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
10
Explain why it is impossible to give the Möbius strip a continuous orientation.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
11
Compute the flux of the vector field 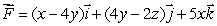 through the surface S, where S is the part of the plane z = x + 2y above the rectangle
through the surface S, where S is the part of the plane z = x + 2y above the rectangle 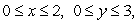 oriented upward.
oriented upward.
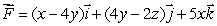 through the surface S, where S is the part of the plane z = x + 2y above the rectangle
through the surface S, where S is the part of the plane z = x + 2y above the rectangle 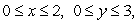 oriented upward.
oriented upward.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
12
Let S be the sphere of radius 6 centered at the origin, oriented outward.
Let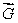 be a vector field such that
be a vector field such that 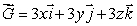 at every point of S.Find the flux of
at every point of S.Find the flux of 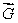 out of S.
out of S.
Let
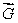 be a vector field such that
be a vector field such that 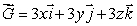 at every point of S.Find the flux of
at every point of S.Find the flux of 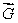 out of S.
out of S.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose S is a disk of radius 2 in the plane x + z = 0 centered at (0, 0, 0)oriented "upward".Write down an area vector for the surface S.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
14
If the surface area of surface S1 is larger than the surface area of surface S2, then .

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose S is a disk of radius 4 in the plane x + z = 0 centered at (0, 0, 0)oriented "upward".Calculate the flux of 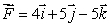 through S.
through S.
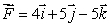 through S.
through S.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
16
Let S be an oriented surface with surface area 6.Suppose is a constant vector field with magnitude 3.If the angle between and is /6 at each point of the surface S, determine the value of the flux integral .

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
17
Let S be the sphere of radius 4 centered at the origin, oriented outward. Find , the unit normal vector to S in the direction of orientation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
18
Let 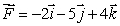 , and let S1 be a horizontal rectangle with corners at (0,0,1), (0,2,1), (3,0,1)and (3,2,1), oriented upward; S2 a rectangle parallel to the xz-plane, with corners at (1,3,1), (2,3,1), (1,3,5)and (2,3,5), oriented in the positive y-direction, and S3 a rectangle parallel to the yz-plane, with corners at (1,2,1), (1,4,1), (1,2,5)and (1,4,5), oriented in the negative x-direction.
, and let S1 be a horizontal rectangle with corners at (0,0,1), (0,2,1), (3,0,1)and (3,2,1), oriented upward; S2 a rectangle parallel to the xz-plane, with corners at (1,3,1), (2,3,1), (1,3,5)and (2,3,5), oriented in the positive y-direction, and S3 a rectangle parallel to the yz-plane, with corners at (1,2,1), (1,4,1), (1,2,5)and (1,4,5), oriented in the negative x-direction.
Arrange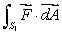 ,
, 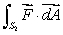 and
and 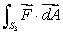 in ascending order.
in ascending order.
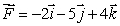 , and let S1 be a horizontal rectangle with corners at (0,0,1), (0,2,1), (3,0,1)and (3,2,1), oriented upward; S2 a rectangle parallel to the xz-plane, with corners at (1,3,1), (2,3,1), (1,3,5)and (2,3,5), oriented in the positive y-direction, and S3 a rectangle parallel to the yz-plane, with corners at (1,2,1), (1,4,1), (1,2,5)and (1,4,5), oriented in the negative x-direction.
, and let S1 be a horizontal rectangle with corners at (0,0,1), (0,2,1), (3,0,1)and (3,2,1), oriented upward; S2 a rectangle parallel to the xz-plane, with corners at (1,3,1), (2,3,1), (1,3,5)and (2,3,5), oriented in the positive y-direction, and S3 a rectangle parallel to the yz-plane, with corners at (1,2,1), (1,4,1), (1,2,5)and (1,4,5), oriented in the negative x-direction.Arrange
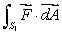 ,
, 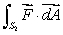 and
and 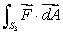 in ascending order.
in ascending order.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
19
Let be the unit normal vector of S.If the angle between and is less than /2 at each point of the surface, then

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
20
If , then is perpendicular to the surface S at every point.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
21
(a)Compute the flux of the vector field 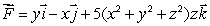 through Sa, the sphere of radius a,
through Sa, the sphere of radius a, 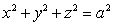 , oriented outward.
, oriented outward.
(b)Find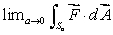 .
.
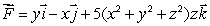 through Sa, the sphere of radius a,
through Sa, the sphere of radius a, 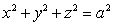 , oriented outward.
, oriented outward.(b)Find
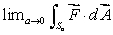 .
.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose the surface S is the part of the surface x = g(y, z), for points (y, z)belonging to a region R in the yz-plane.If S is oriented in the positive x-direction, what will be the formula for computing the flux of 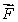 through S?
through S?
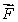 through S?
through S?
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
23
Let .Write down an iterated integral that computes the flux of through S, where S is the part of the surface below the plane z = 16, oriented downward.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
24
Compute the flux of 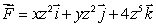 through the cylindrical surface
through the cylindrical surface 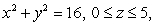 oriented away from the z-axis.
oriented away from the z-axis.
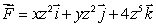 through the cylindrical surface
through the cylindrical surface 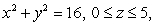 oriented away from the z-axis.
oriented away from the z-axis.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate , where and S is the part of the cylinder with x 0, y 0, 0 z 2, oriented toward the z-axis.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
26
Compute the flux of the vector field 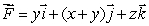 through the surface S that is the part of the surface
through the surface S that is the part of the surface 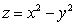 above the disk
above the disk 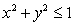 , oriented in the positive z-direction.
, oriented in the positive z-direction.
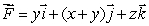 through the surface S that is the part of the surface
through the surface S that is the part of the surface 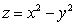 above the disk
above the disk 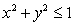 , oriented in the positive z-direction.
, oriented in the positive z-direction.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
27
Find the flux of 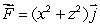 through the disk of radius 5 in the xz-plane, centered at the origin, and oriented upward.Give an exact answer.
through the disk of radius 5 in the xz-plane, centered at the origin, and oriented upward.Give an exact answer.
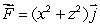 through the disk of radius 5 in the xz-plane, centered at the origin, and oriented upward.Give an exact answer.
through the disk of radius 5 in the xz-plane, centered at the origin, and oriented upward.Give an exact answer.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
28
Let S be the spherical region of radius R with /3 2 /3 and /3 2 /3.Find the value of R so that Give your answer to two decimal places.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
29
Let .Write down an iterated integral that computes the flux of through S, where S is the part of the cylinder with x 0, y 0, 0 z 4, bounded between the planes y = 0 and y = x, oriented outward.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
30
A greenhouse is in the shape of the graph 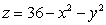 with the floor at z = 0.Suppose the temperature around the greenhouse is given by
with the floor at z = 0.Suppose the temperature around the greenhouse is given by 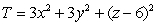 .Let
.Let 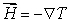 be the heat flux density field.
be the heat flux density field.
Calculate the total heat flux outward across the boundary wall of the greenhouse.
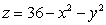 with the floor at z = 0.Suppose the temperature around the greenhouse is given by
with the floor at z = 0.Suppose the temperature around the greenhouse is given by 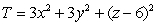 .Let
.Let 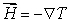 be the heat flux density field.
be the heat flux density field.Calculate the total heat flux outward across the boundary wall of the greenhouse.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
31
If is a constant vector field and S1 and S2 are oriented rectangles with areas 1 and 2 respectively, then .

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
32
Let S be the part of the sphere with x 0, y 0, z 0, oriented outward.Evaluate .

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
33
Let 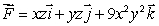 .Calculate the flux of
.Calculate the flux of 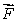 through the surface oriented upward and given by z = f(x, y)= xy, over the region in the xy-plane bounded by the curves
through the surface oriented upward and given by z = f(x, y)= xy, over the region in the xy-plane bounded by the curves 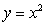 and
and 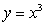 between the origin and the point (1, 1).
between the origin and the point (1, 1).
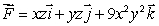 .Calculate the flux of
.Calculate the flux of 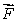 through the surface oriented upward and given by z = f(x, y)= xy, over the region in the xy-plane bounded by the curves
through the surface oriented upward and given by z = f(x, y)= xy, over the region in the xy-plane bounded by the curves 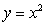 and
and 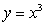 between the origin and the point (1, 1).
between the origin and the point (1, 1).
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
34
Compute the flux of the vector field 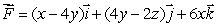 through the surface S, where S is the part of the plane z = x + 2y above the rectangle
through the surface S, where S is the part of the plane z = x + 2y above the rectangle 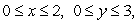 oriented upward.
oriented upward.
What is the answer if the plane is oriented downward?
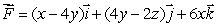 through the surface S, where S is the part of the plane z = x + 2y above the rectangle
through the surface S, where S is the part of the plane z = x + 2y above the rectangle 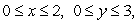 oriented upward.
oriented upward.What is the answer if the plane is oriented downward?

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
35
Let C be the portion of the cylinder of fixed radius R with /3 2 /3 and -a z a oriented outward for some positive number a.Let S be the portion of the sphere with /3 2 /3 and /3 2 /3 oriented outward.Determine the value of a for which the flux of through each of these surfaces is equal in magnitude but opposite in sign for any choice of R.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
36
If and S is an oriented surface, then .

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
37
Compute the flux of the vector field 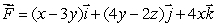 through the surface S, where S is the part of the plane z = x + 2y above the rectangle
through the surface S, where S is the part of the plane z = x + 2y above the rectangle 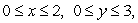 oriented downward.
oriented downward.
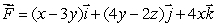 through the surface S, where S is the part of the plane z = x + 2y above the rectangle
through the surface S, where S is the part of the plane z = x + 2y above the rectangle 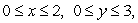 oriented downward.
oriented downward.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
38
Let 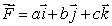 be a constant vector field and S be an oriented surface.
be a constant vector field and S be an oriented surface.
Show that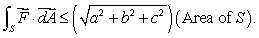
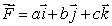 be a constant vector field and S be an oriented surface.
be a constant vector field and S be an oriented surface.Show that
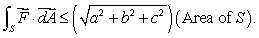

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
39
Calculate where C is a cylinder of radius R with 0 z 1.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
40
If is a constant vector field and S1 and S2 are oriented rectangles with areas 3 and 15 respectively, both orientated with the vector is it true that ?

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
41
Calculate the flux of 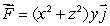 through the disk
through the disk 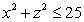 on the plane
on the plane 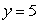 , oriented in the positive y-direction.
, oriented in the positive y-direction.
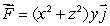 through the disk
through the disk 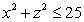 on the plane
on the plane 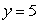 , oriented in the positive y-direction.
, oriented in the positive y-direction.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
42
Calculate the flux of , through the plane rectangle z = 3, 0 x 2, 0 y 5, oriented in the positive z-direction.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
43
Let S be the cylinder 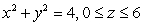 .Find Q if
.Find Q if 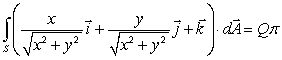 .
.
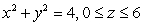 .Find Q if
.Find Q if 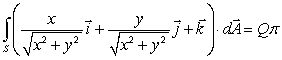 .
.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
44
Calculate the flux of through the plane rectangle z= 1, 0 x 5, 0 y 2, oriented downward.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
45
Calculate the flux of 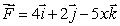 through a disk of radius 5 in the plane x = 3, oriented away from the origin.
through a disk of radius 5 in the plane x = 3, oriented away from the origin.
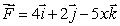 through a disk of radius 5 in the plane x = 3, oriented away from the origin.
through a disk of radius 5 in the plane x = 3, oriented away from the origin.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
46
Let 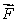 be a constant vector field with
be a constant vector field with 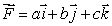 , where a, b, c are constants satisfying the condition
, where a, b, c are constants satisfying the condition 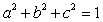 .Let S be a surface lying on the plane x + 4y - 5z = 10 oriented upward.
.Let S be a surface lying on the plane x + 4y - 5z = 10 oriented upward.
If the surface area of S is 10, what is the smallest possible value of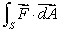 , and what are the corresponding values of a, b, c?
, and what are the corresponding values of a, b, c?
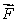 be a constant vector field with
be a constant vector field with 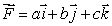 , where a, b, c are constants satisfying the condition
, where a, b, c are constants satisfying the condition 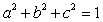 .Let S be a surface lying on the plane x + 4y - 5z = 10 oriented upward.
.Let S be a surface lying on the plane x + 4y - 5z = 10 oriented upward.If the surface area of S is 10, what is the smallest possible value of
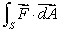 , and what are the corresponding values of a, b, c?
, and what are the corresponding values of a, b, c?
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
47
Suppose that S is the surface which is a portion of the graph of a smooth function 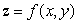 over a region R in the xy-plane, oriented upward.Consider the vector field
over a region R in the xy-plane, oriented upward.Consider the vector field 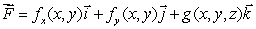 .
.
Find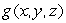 so that
so that 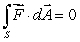 .
.
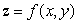 over a region R in the xy-plane, oriented upward.Consider the vector field
over a region R in the xy-plane, oriented upward.Consider the vector field 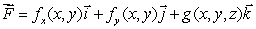 .
.Find
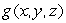 so that
so that 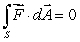 .
.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose T is the triangle with vertices 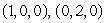 and
and 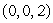 oriented upward.Calculate the flux of
oriented upward.Calculate the flux of 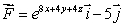 through T exactly, and then give an answer rounded to 3 decimal places.
through T exactly, and then give an answer rounded to 3 decimal places.
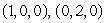 and
and 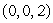 oriented upward.Calculate the flux of
oriented upward.Calculate the flux of 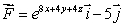 through T exactly, and then give an answer rounded to 3 decimal places.
through T exactly, and then give an answer rounded to 3 decimal places.
Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
49
Find the flux of over the sphere Sa, , oriented outward, with a > 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
50
Let .
True or False: The flux of through any cylinder C (with )does not depend on the radius R.
True or False: The flux of through any cylinder C (with )does not depend on the radius R.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
51
Calculate the flux of , through the plane rectangle y = 4, 0 x 4, 0 z 5, oriented in the positive y-direction.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck
52
Calculate the flux of through the plane rectangle y = 1, 0 x 1, 0 z 3, oriented in the negative y-direction.

Unlock Deck
Unlock for access to all 52 flashcards in this deck.
Unlock Deck
k this deck


