Deck 16: Integrating Functions of Several Variables
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 16: Integrating Functions of Several Variables
1
Set up but do not evaluate a (multiple)integral that gives the volume of the solid bounded above by the sphere and below by the paraboloid .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
2
Estimate R f(x, y)dA using the table of values below, where R is the rectangle 0 x 4, 0 y 6
165
3
Upper and lower sums for a function f on a rectangle R, using n subdivisions on each side, are 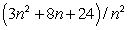 and
and 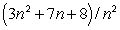 respectively.Evaluate
respectively.Evaluate 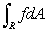
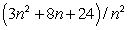 and
and 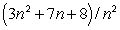 respectively.Evaluate
respectively.Evaluate 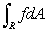
3
4
Consider the integral Rewrite the integral with the integration performed in the opposite order.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the iterated integral. 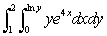
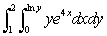

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
Calculate the following integral exactly.(Your answer should not be a decimal approximating the true answer, but should be exactly equal to the true answer.Your answer may contain e, , , and so on.)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
Let R be the region in the first quadrant bounded by the x- and y-axes and the line x + y = 7.Evaluate 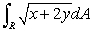 exactly and then give an answer rounded to 4 decimal places.
exactly and then give an answer rounded to 4 decimal places.
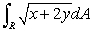 exactly and then give an answer rounded to 4 decimal places.
exactly and then give an answer rounded to 4 decimal places.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the iterated integral. 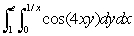
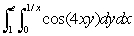

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
Reverse the order of integration for the following integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate 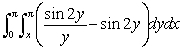 by first reversing the order of integration.
by first reversing the order of integration.
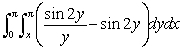 by first reversing the order of integration.
by first reversing the order of integration.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
Let f(x, y)be a positive function of x and y which is independent of x, that is, f(x, y)= g(y)for some one-variable function g.Suppose that and .
Find , where R is the rectangle 0 x 3, 0 y 10.
Find , where R is the rectangle 0 x 3, 0 y 10.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
Let R1 be the region 0 x 3, -2 y 4, and let R2 be the region 3 x 5, -2 y 4.Suppose that the average value of f over R1 is 6 and the average value over R2 is 7.
Find the average value of f over R, .
Find the average value of f over R, .

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
True or false?
If f is any two-variable function, then , where R is the rectangle 0 x 2, 0 y 1 and S is the square 0 x, y 1.
If f is any two-variable function, then , where R is the rectangle 0 x 2, 0 y 1 and S is the square 0 x, y 1.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
Find the volume of the region under the graph of 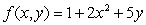 and above the region
and above the region 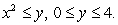
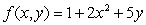 and above the region
and above the region 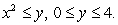

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
Find a region R such that double integral has the largest value.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
Find the volume under the graph of 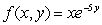 lying over the triangle with vertices (0, 0), (2, 2)and (4, 0).
lying over the triangle with vertices (0, 0), (2, 2)and (4, 0).
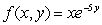 lying over the triangle with vertices (0, 0), (2, 2)and (4, 0).
lying over the triangle with vertices (0, 0), (2, 2)and (4, 0).
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
Reverse the order of integration for the following integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
Calculate the following integral exactly.(Your answer should not be a decimal approximating the true answer, but should be exactly equal to the true answer.Your answer may contain e, , , and so on.)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
The function 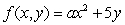 has an average value of 4 on the triangle with vertices at (0, 0), (0, 1)and (1, 0).Find the constant a.
has an average value of 4 on the triangle with vertices at (0, 0), (0, 1)and (1, 0).Find the constant a.
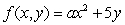 has an average value of 4 on the triangle with vertices at (0, 0), (0, 1)and (1, 0).Find the constant a.
has an average value of 4 on the triangle with vertices at (0, 0), (0, 1)and (1, 0).Find the constant a.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
Calculate the following integral exactly.(Your answer should not be a decimal approximating the true answer, but should be exactly equal to the true answer.Your answer may contain e, , , and so on.)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
Set up an iterated integral for , where W is the solid region bounded below by the rectangle 0 x 3, 0 y 1 and above by the surface
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
A cylindrical tube of radius 2cm and length 3cm contains a gas.As the tube spins around its axis, the density of the gas increases as you get farther from the axis.The density, D, at a distance of r cm from the axis is D(r)= 1 +9 r gm/cc.
Write a triple integral representing the total mass of the gas in the tube and evaluate the integral.
Write a triple integral representing the total mass of the gas in the tube and evaluate the integral.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
Set up (but do not evaluate)an iterated integral to compute the mass of the solid paraboloid bounded by and z = 1, if the density is given by (x, y, z)= z2.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
Compute the area of the flower-like region bounded by r = 6 + 3 cos (8 ).

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
Find the triple integral of the function f(x, y, z)= xy sin (18yz)over the rectangular box 0 x , 0 y 1, 0 z /6.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
Set up the three-dimensional integral where R is the "ice-cream cone" enclosed by a sphere of radius 2 centered at the origin and the cone .Use rectangular coordinates. 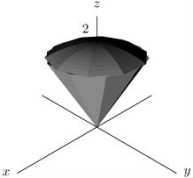
A)
B)
C)

A)
B)
C)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the volume between a cone centered along the positive z-axis, with vertex at the origin and containing the point (0, 1, 1), and a sphere of radius 3 centered at the origin.
Write a triple integral which represents this volume and evaluate it.Use spherical coordinates.
Write a triple integral which represents this volume and evaluate it.Use spherical coordinates.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
Calculate the following integral: 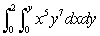
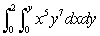

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
Calculate the following integral: 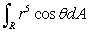 where R is the shaded region shown below.
where R is the shaded region shown below.
·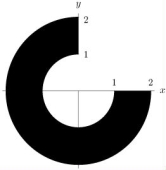
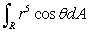 where R is the shaded region shown below.
where R is the shaded region shown below.·


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
Suppose a solid is the region in three-space in the first octant bounded by the plane x + y = 1 and the cylinder 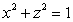 .If the density of this solid at a point (x, y, z)is given by
.If the density of this solid at a point (x, y, z)is given by 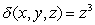 , find its mass.
, find its mass.
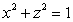 .If the density of this solid at a point (x, y, z)is given by
.If the density of this solid at a point (x, y, z)is given by 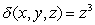 , find its mass.
, find its mass.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
A solid is bounded below by the triangle z = 0, x 0, y 0, x + y 1 and above by the plane z = x + 6y + 2.If the density of the solid is given by (x, y, z)= z, find its mass.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate 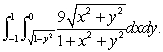 Provide an exact answer.
Provide an exact answer.
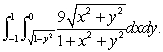 Provide an exact answer.
Provide an exact answer.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
For the following region, decide whether to integrate using polar or Cartesian coordinates.Write an iterated integral of an arbitrary function f(x, y)over the region. 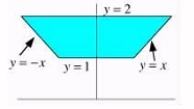


Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate the integral 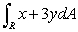 , where R is the region in the first quadrant bounded by the y-axis, the line y = x and the circles
, where R is the region in the first quadrant bounded by the y-axis, the line y = x and the circles 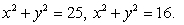
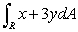 , where R is the region in the first quadrant bounded by the y-axis, the line y = x and the circles
, where R is the region in the first quadrant bounded by the y-axis, the line y = x and the circles 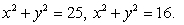

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
Let R be the ice-cream cone lying inside the sphere 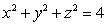 and inside the cone
and inside the cone 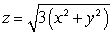 .Find the center of mass of R.
.Find the center of mass of R.
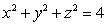 and inside the cone
and inside the cone 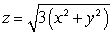 .Find the center of mass of R.
.Find the center of mass of R.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
Evaluate exactly the integral 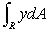 , where R is the region shown below.
, where R is the region shown below. 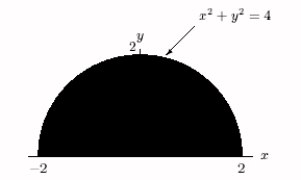
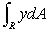 , where R is the region shown below.
, where R is the region shown below. 

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Sketch the region of integration of the following integral and then convert the expression to polar co-ordinates (you do not have to evaluate it). 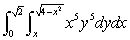
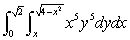

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate the iterated integral 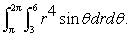
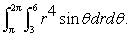

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
Find the volume of the solid bounded by the paraboloid 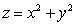 and the plane z = 1.
and the plane z = 1.
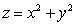 and the plane z = 1.
and the plane z = 1.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
Convert the integral 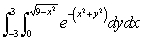 to polar coordinates and hence evaluate it exactly.
to polar coordinates and hence evaluate it exactly.
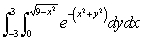 to polar coordinates and hence evaluate it exactly.
to polar coordinates and hence evaluate it exactly.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
Let x and y have joint density function 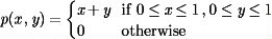 Find the probability that x > y +0.4.
Find the probability that x > y +0.4.
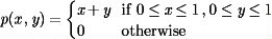 Find the probability that x > y +0.4.
Find the probability that x > y +0.4.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
Choose the most appropriate coordinate system and set up a triple integral, including limits of integration, for a density function f(x, y, z)over the given region. 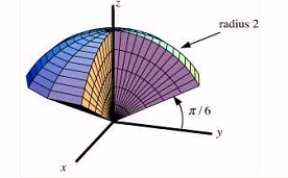
A)spherical coordinates
B)cylindrical coordinates
C)rectangular coordinates
D)None of the above.

A)spherical coordinates
B)cylindrical coordinates
C)rectangular coordinates
D)None of the above.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate the integral 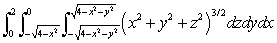 in spherical coordinates.
in spherical coordinates.
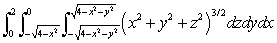 in spherical coordinates.
in spherical coordinates.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
Evaluate 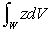 where W is the first octant portion of the ball of radius 3 centered at the origin.
where W is the first octant portion of the ball of radius 3 centered at the origin.
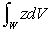 where W is the first octant portion of the ball of radius 3 centered at the origin.
where W is the first octant portion of the ball of radius 3 centered at the origin.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
Let W be the region between the cylinders 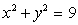 and
and 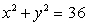 in the first octant and under the plane z = 1.Evaluate
in the first octant and under the plane z = 1.Evaluate 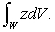
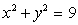 and
and 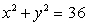 in the first octant and under the plane z = 1.Evaluate
in the first octant and under the plane z = 1.Evaluate 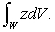

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
Rewrite the integral 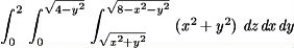 in spherical coordinates.You do not have to evaluate the integral.
in spherical coordinates.You do not have to evaluate the integral.
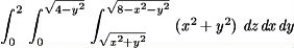 in spherical coordinates.You do not have to evaluate the integral.
in spherical coordinates.You do not have to evaluate the integral.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the integral by interchanging the order of integration. 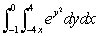 .
.
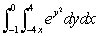 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
Let x and y have joint density function Find the probability that 0.5 x 0.6.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the change of variables x = s + 3t, y = s - 2t.
Let R be the region bounded by the lines 2x + 3y = 1, 2x + 3y = 4, x - y = -3, and x - y = 2.Find the region T in the st-plane that corresponds to region R.
Use the change of variables to evaluate
Let R be the region bounded by the lines 2x + 3y = 1, 2x + 3y = 4, x - y = -3, and x - y = 2.Find the region T in the st-plane that corresponds to region R.
Use the change of variables to evaluate

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
The joint density function for x, y is given by 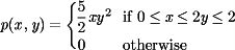 Find the probability that (x, y)satisfies
Find the probability that (x, y)satisfies 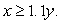
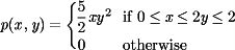 Find the probability that (x, y)satisfies
Find the probability that (x, y)satisfies 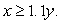

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
An arrow strikes a circular target at random at a point (x, y), using a coordinate system with origin at the center of the target.The probability density function for the point where the arrow strikes is given by 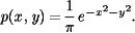 What is the probability that the arrow strikes within 0.45 feet of the center of the target.
What is the probability that the arrow strikes within 0.45 feet of the center of the target.
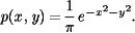 What is the probability that the arrow strikes within 0.45 feet of the center of the target.
What is the probability that the arrow strikes within 0.45 feet of the center of the target.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
Find the mass of the solid cylinder 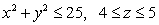 with density function
with density function 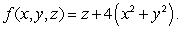
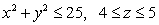 with density function
with density function 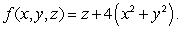

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the integral 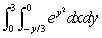 .Give your answer to two decimal places.
.Give your answer to two decimal places.
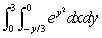 .Give your answer to two decimal places.
.Give your answer to two decimal places.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
Find the condition on the non-negative constants a and b for p(x, y)to be a joint density function, where
A)
B)
C)
D)a=b
E)
A)
B)
C)
D)a=b
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the change of variables x = s + 5t, y = s - 3t.
Find the absolute value of the Jacobian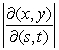 .
.
Find the absolute value of the Jacobian
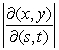 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
Let R be the region bounded between the two ellipses and Use this change of coordinates for to evaluate the integral
A)240
B)3240
C)162
D)1620
E)1620
A)240
B)3240
C)162
D)1620
E)1620

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
Jane and Mary will meet outside the library at noon.Jane's arrival time is x and Mary's arrival time is y, where x and y are measured in minutes after noon.The probability density function for the variation in x and y is 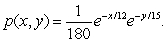 After Jane arrives, she will wait up to 15 minutes for Mary, but Mary won't wait for Jane.Find the probability that they meet.
After Jane arrives, she will wait up to 15 minutes for Mary, but Mary won't wait for Jane.Find the probability that they meet.
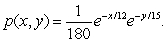 After Jane arrives, she will wait up to 15 minutes for Mary, but Mary won't wait for Jane.Find the probability that they meet.
After Jane arrives, she will wait up to 15 minutes for Mary, but Mary won't wait for Jane.Find the probability that they meet.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the integral 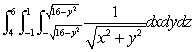 in cylindrical coordinates.
in cylindrical coordinates.
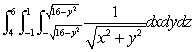 in cylindrical coordinates.
in cylindrical coordinates.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
The region W is shown below.Write the limits of integration for in spherical coordinates. 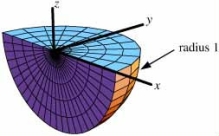
A)
B)
C)

A)
B)
C)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
Let R be the region in the first quadrant bounded between the circle 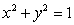 and the two axes.Then
and the two axes.Then 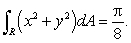 Let
Let 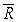 be the region in the first quadrant bounded between the ellipse
be the region in the first quadrant bounded between the ellipse 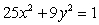 and the two axes.
and the two axes.
Use the change of variable x = s/5, y = t/3 to evaluate the integral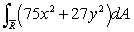
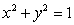 and the two axes.Then
and the two axes.Then 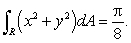 Let
Let 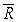 be the region in the first quadrant bounded between the ellipse
be the region in the first quadrant bounded between the ellipse 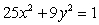 and the two axes.
and the two axes.Use the change of variable x = s/5, y = t/3 to evaluate the integral
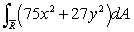

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
The joint density function for random variables x and y is 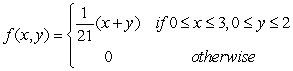 Find the probability
Find the probability 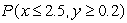 .Give your answer to 3 decimal places.
.Give your answer to 3 decimal places.
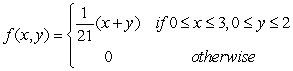 Find the probability
Find the probability 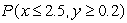 .Give your answer to 3 decimal places.
.Give your answer to 3 decimal places.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
If f and g are two continuous functions on a region R, then .

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Consider the integral 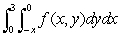 .
.
(a)Sketch the region of integration and rewrite the integral with order of integration reversed.
(b)Rewrite the integral in polar coordinates.
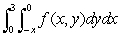 .
.(a)Sketch the region of integration and rewrite the integral with order of integration reversed.
(b)Rewrite the integral in polar coordinates.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
The joint density function for x, y is given by Write down an iterated integral to compute the probability that x + y 10.You do not need to do the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
Let W be the part of the solid sphere of radius 4, centered at the origin, that lies above the plane z = 2.Express in
(a)Cartesian
(b)Cylindrical
(c)Spherical coordinates.
(a)Cartesian
(b)Cylindrical
(c)Spherical coordinates.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the integral 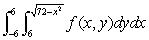 .Convert the integral to polar coordinates.
.Convert the integral to polar coordinates.
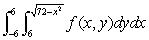 .Convert the integral to polar coordinates.
.Convert the integral to polar coordinates.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate the integral 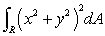 , where R is the region shown below.
, where R is the region shown below. 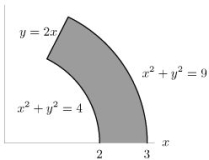
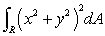 , where R is the region shown below.
, where R is the region shown below. 

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
Consider the region in 3-space bounded by the surface 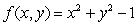 and the plane
and the plane 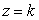 where
where 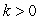 .Find the value of k such that the volume of this region below the xy-plane equals the volume of this region above the xy-plane.
.Find the value of k such that the volume of this region below the xy-plane equals the volume of this region above the xy-plane.
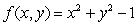 and the plane
and the plane 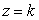 where
where 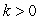 .Find the value of k such that the volume of this region below the xy-plane equals the volume of this region above the xy-plane.
.Find the value of k such that the volume of this region below the xy-plane equals the volume of this region above the xy-plane.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
Convert the integral to polar coordinates.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate the integral 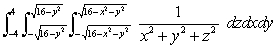 in spherical coordinates.
in spherical coordinates.
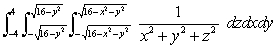 in spherical coordinates.
in spherical coordinates.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
Find the mass of the solid cylinder 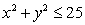 ,
, 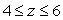 with density function
with density function 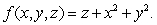
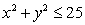 ,
, 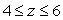 with density function
with density function 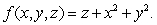

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
Find the area of the part of the hyperbolic paraboloid that lies between the cylinders and .
A)
B)
C)
D)
E)
A)

B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate the integral 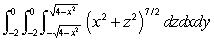 in cylindrical coordinates.
in cylindrical coordinates.
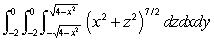 in cylindrical coordinates.
in cylindrical coordinates.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
The function 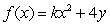 has an average value of 16 on the rectangle with vertices at (0, 0),(0, 2), (2, 0)and (2, 2).Find the constant k.
has an average value of 16 on the rectangle with vertices at (0, 0),(0, 2), (2, 0)and (2, 2).Find the constant k.
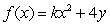 has an average value of 16 on the rectangle with vertices at (0, 0),(0, 2), (2, 0)and (2, 2).Find the constant k.
has an average value of 16 on the rectangle with vertices at (0, 0),(0, 2), (2, 0)and (2, 2).Find the constant k.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Let W be the region between the spheres and .Given that , evaluate the integral , where is the region between the ellipsoids and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Find the condition on the non-negative constants a and b for p(x, y)to be a joint density function, where 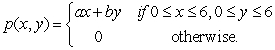
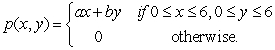

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


