Exam 16: Integrating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Reverse the order of integration for the following integral.
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
E
Evaluate the integral , where R is the region shown below. 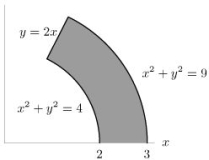
Free
(Essay)
4.9/5  (41)
(41)
Correct Answer:
Find the volume under the graph of lying over the triangle with vertices (0, 0), (2, 2)and (4, 0).
(Essay)
4.8/5  (31)
(31)
Evaluate where W is the first octant portion of the ball of radius 3 centered at the origin.
(Essay)
4.8/5  (39)
(39)
The joint density function for x, y is given by Find the probability that (x, y)satisfies
(Short Answer)
4.7/5  (37)
(37)
Calculate the following integral exactly.(Your answer should not be a decimal approximating the true answer, but should be exactly equal to the true answer.Your answer may contain e, , , and so on.)
(Essay)
4.8/5  (35)
(35)
Consider the integral .
(a)Sketch the region of integration and rewrite the integral with order of integration reversed.
(b)Rewrite the integral in polar coordinates.
(Essay)
4.8/5  (35)
(35)
Let R be the region in the first quadrant bounded between the circle and the two axes.Then Let be the region in the first quadrant bounded between the ellipse and the two axes.
Use the change of variable x = s/5, y = t/3 to evaluate the integral
(Essay)
4.9/5  (41)
(41)
True or false?
If f is any two-variable function, then , where R is the rectangle 0 x 2, 0 y 1 and S is the square 0 x, y 1.
(True/False)
5.0/5  (32)
(32)
Find the triple integral of the function f(x, y, z)= xy sin (18yz)over the rectangular box 0 x , 0 y 1, 0 z /6.
(Essay)
4.9/5  (42)
(42)
Consider the region in 3-space bounded by the surface and the plane where .Find the value of k such that the volume of this region below the xy-plane equals the volume of this region above the xy-plane.
(Essay)
4.8/5  (43)
(43)
Calculate the following integral exactly.(Your answer should not be a decimal approximating the true answer, but should be exactly equal to the true answer.Your answer may contain e, , , and so on.)
(Multiple Choice)
4.8/5  (34)
(34)
Suppose a solid is the region in three-space in the first octant bounded by the plane x + y = 1 and the cylinder .If the density of this solid at a point (x, y, z)is given by , find its mass.
(Essay)
4.9/5  (40)
(40)
A cylindrical tube of radius 2cm and length 3cm contains a gas.As the tube spins around its axis, the density of the gas increases as you get farther from the axis.The density, D, at a distance of r cm from the axis is D(r)= 1 +9 r gm/cc.
Write a triple integral representing the total mass of the gas in the tube and evaluate the integral.
(Essay)
4.9/5  (36)
(36)
Let R be the region in the first quadrant bounded by the x- and y-axes and the line x + y = 7.Evaluate exactly and then give an answer rounded to 4 decimal places.
(Essay)
5.0/5  (33)
(33)
Showing 1 - 20 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)