Deck 18: Line Integrals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/78
Play
Full screen (f)
Deck 18: Line Integrals
1
Let C be a segment 9 units long of the contour f(x, y)= 5.What is the work done by the gradient field of f along C?
0
2
Given the graph of the vector field, 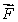 , shown below, list the following quantities in increasing order:
, shown below, list the following quantities in increasing order: 
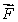 , shown below, list the following quantities in increasing order:
, shown below, list the following quantities in increasing order: 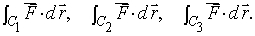

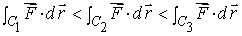
3
If the length of curve C1 is longer than the length of curve C2, then
False
4
Find 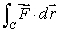 where
where 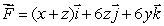 and C is the line from the point (2, 4, 4)to the point (0, 6, -8).
and C is the line from the point (2, 4, 4)to the point (0, 6, -8).
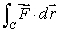 where
where 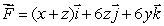 and C is the line from the point (2, 4, 4)to the point (0, 6, -8).
and C is the line from the point (2, 4, 4)to the point (0, 6, -8).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that 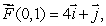
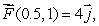
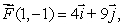 and
and 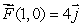 .
.
Estimate the work done by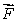 along the line from (1, 0)to (1, 1).
along the line from (1, 0)to (1, 1).
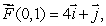
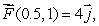
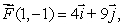 and
and 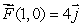 .
.Estimate the work done by
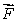 along the line from (1, 0)to (1, 1).
along the line from (1, 0)to (1, 1).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
6
Find, by direct computation, the line integral of 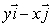 around the circle
around the circle 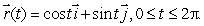
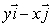 around the circle
around the circle 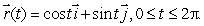

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
7
Suppose that , where C is the circle of radius 1, centered at the origin, starting at (1, 0)and traveling counter-clockwise back to (1, 0).

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
8
Calculate 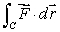 when
when 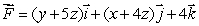 and C is the line from the origin to the point (4, 4, 4).
and C is the line from the origin to the point (4, 4, 4).
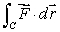 when
when 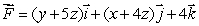 and C is the line from the origin to the point (4, 4, 4).
and C is the line from the origin to the point (4, 4, 4).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
9
Explain in words and symbols how to calculate the line integral 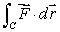 given a parameterization,
given a parameterization, 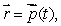 of the curve C.
of the curve C.
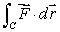 given a parameterization,
given a parameterization, 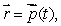 of the curve C.
of the curve C.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate 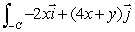 , where C is the triangular path from (0, 0)to (1, 1)to (0, 1)to (0, 0).
, where C is the triangular path from (0, 0)to (1, 1)to (0, 1)to (0, 0).
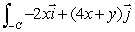 , where C is the triangular path from (0, 0)to (1, 1)to (0, 1)to (0, 0).
, where C is the triangular path from (0, 0)to (1, 1)to (0, 1)to (0, 0).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose that 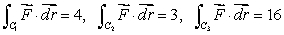 and
and 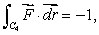 where C1 is the line joining (0, 0)to (1, 0), C2 is the line joining (0, 0)to (3, 0), C3 is the line joining (0, 0)to (0, 1)and C4 is the line joining (0, 1)to (0, 2).
where C1 is the line joining (0, 0)to (1, 0), C2 is the line joining (0, 0)to (3, 0), C3 is the line joining (0, 0)to (0, 1)and C4 is the line joining (0, 1)to (0, 2).
Determine, if possible, the value of the line integral of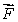 along the line from (0, 1)to (1, 0).If the value cannot be determined, say so.
along the line from (0, 1)to (1, 0).If the value cannot be determined, say so.
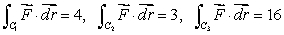 and
and 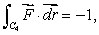 where C1 is the line joining (0, 0)to (1, 0), C2 is the line joining (0, 0)to (3, 0), C3 is the line joining (0, 0)to (0, 1)and C4 is the line joining (0, 1)to (0, 2).
where C1 is the line joining (0, 0)to (1, 0), C2 is the line joining (0, 0)to (3, 0), C3 is the line joining (0, 0)to (0, 1)and C4 is the line joining (0, 1)to (0, 2).Determine, if possible, the value of the line integral of
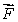 along the line from (0, 1)to (1, 0).If the value cannot be determined, say so.
along the line from (0, 1)to (1, 0).If the value cannot be determined, say so.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
12
Let be a vector field with constant magnitude Suppose that 0 t 5, is a parameterization of a flow line C of .
Find
Find

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
13
Let Is the line integral of around the unit circle traversed counterclockwise: positive, negative, or zero?
A)Positive
B)Negative
C)Zero
A)Positive
B)Negative
C)Zero

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
14
Let 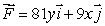 and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
Find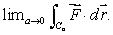
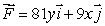 and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.Find
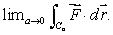

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
15
Let be the constant vector field Calculate the line integral of along a line segment L of length 9 at an angle /3 to

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
16
Let 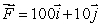 and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
Find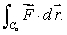
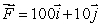 and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.Find

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
17
Let C1 be the rectangular loop consisting of four line segments: from (0, 0)to (1, 0), then to (1, 2), then to (0, 2), then back to (0, 0).Suppose C2 is the triangular loop joining (0, 0)to (1, 0), then to (1, 2)then back to (0, 0), and C3 is another triangular loop joining (0, 0)to (1, 2), then to (0, 2)and then back to (0, 0). Is it true that for any vector field defined on the xy-plane?
A)Not possible to decide
B)Yes
C)No
A)Not possible to decide
B)Yes
C)No

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the vector field 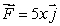 .
.
Without using parametrization, calculate directly the line integral of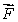 along the line from (3, 3)to (7, 3).
along the line from (3, 3)to (7, 3).
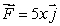 .
.Without using parametrization, calculate directly the line integral of
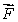 along the line from (3, 3)to (7, 3).
along the line from (3, 3)to (7, 3).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
19
If , then is perpendicular to the curve C at every point.

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
20
Let C be the curve described by .If the angle between and is less than /2, then

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
21
Find a vector field 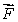 with the property that the line integral of
with the property that the line integral of 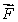 along the line from (0, 0)to (a, b)is
along the line from (0, 0)to (a, b)is 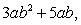 for any numbers a and b.
for any numbers a and b.
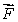 with the property that the line integral of
with the property that the line integral of 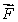 along the line from (0, 0)to (a, b)is
along the line from (0, 0)to (a, b)is 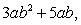 for any numbers a and b.
for any numbers a and b.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the vector field 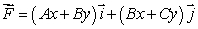 for certain constants A, B and C.
for certain constants A, B and C.
Use the definition of the line integral to evaluate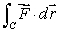 , where C is the line from (1, 0)to (11, 1).
, where C is the line from (1, 0)to (11, 1).
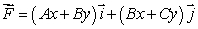 for certain constants A, B and C.
for certain constants A, B and C.Use the definition of the line integral to evaluate
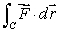 , where C is the line from (1, 0)to (11, 1).
, where C is the line from (1, 0)to (11, 1).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
23
Let 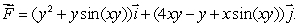 Is
Is 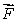 path-independent?
path-independent?
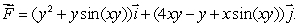 Is
Is 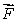 path-independent?
path-independent?
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
24
Given that 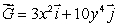 find a function g so that
find a function g so that 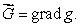 Use the function g to compute
Use the function g to compute 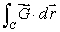 where C is a curve beginning at the point (2, 4)and ending at the point (0, 1).
where C is a curve beginning at the point (2, 4)and ending at the point (0, 1).
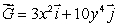 find a function g so that
find a function g so that 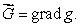 Use the function g to compute
Use the function g to compute 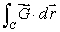 where C is a curve beginning at the point (2, 4)and ending at the point (0, 1).
where C is a curve beginning at the point (2, 4)and ending at the point (0, 1).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
25
Find the work done by the force field 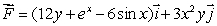 along the parabola y = 2x2 from (0, 0)to (1, 2).
along the parabola y = 2x2 from (0, 0)to (1, 2).
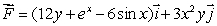 along the parabola y = 2x2 from (0, 0)to (1, 2).
along the parabola y = 2x2 from (0, 0)to (1, 2).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
26
Let 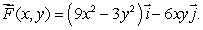 Evaluate the line integral
Evaluate the line integral 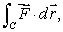 where C the path from (0, 0)to (1, 1)that goes along the x-axis to (1, 0), and then vertically up to (1, 1).
where C the path from (0, 0)to (1, 1)that goes along the x-axis to (1, 0), and then vertically up to (1, 1).
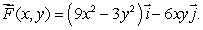 Evaluate the line integral
Evaluate the line integral 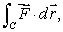 where C the path from (0, 0)to (1, 1)that goes along the x-axis to (1, 0), and then vertically up to (1, 1).
where C the path from (0, 0)to (1, 1)that goes along the x-axis to (1, 0), and then vertically up to (1, 1).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
27
If 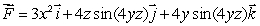 , compute
, compute 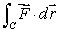 where C is the curve from A(0, 0, 3)to B(2, 1, 5)shown below.
where C is the curve from A(0, 0, 3)to B(2, 1, 5)shown below.
Hint: messy computation can be avoided.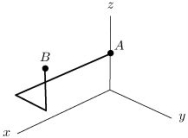
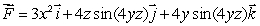 , compute
, compute  where C is the curve from A(0, 0, 3)to B(2, 1, 5)shown below.
where C is the curve from A(0, 0, 3)to B(2, 1, 5)shown below.Hint: messy computation can be avoided.


Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the vector field 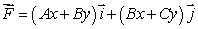 for certain constants A, B and C.
for certain constants A, B and C.
Find the line integral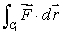 , where C1 is the curve
, where C1 is the curve 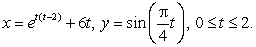
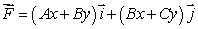 for certain constants A, B and C.
for certain constants A, B and C.Find the line integral
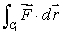 , where C1 is the curve
, where C1 is the curve 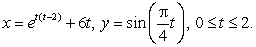

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
29
If is a gradient vector field, then .

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
30
Let 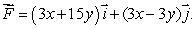 Evaluate
Evaluate 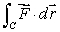 , where C is parameterized by
, where C is parameterized by 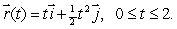
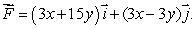 Evaluate
Evaluate 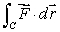 , where C is parameterized by
, where C is parameterized by 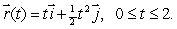

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
31
Let , where (a)Evaluate the line integral , where C is the line from (0, 0)to (2, -4).
(b)Do you expect the line integral of along the parabola y = x2-4x, 0 x 2 to equal to the answer to (a)?
(b)Do you expect the line integral of along the parabola y = x2-4x, 0 x 2 to equal to the answer to (a)?

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
32
Let 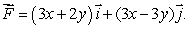 Evaluate
Evaluate 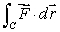 , where C is the line from (0, 0)to (2, 2).
, where C is the line from (0, 0)to (2, 2).
 Evaluate
Evaluate 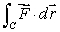 , where C is the line from (0, 0)to (2, 2).
, where C is the line from (0, 0)to (2, 2).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate , where C is the curve for 0 t 1.
Note that the line integral is around -C, not C.
Note that the line integral is around -C, not C.

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
34
Let 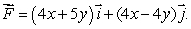 Let
Let 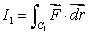 , where C1 is the line from (0, 0)to (2, 2).
, where C1 is the line from (0, 0)to (2, 2).
Let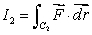 , where C2 is parameterized by
, where C2 is parameterized by 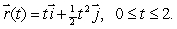 Notice that both C1 and C2 go from (0, 0)to (2, 2), but is
Notice that both C1 and C2 go from (0, 0)to (2, 2), but is 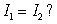 Explain.
Explain.
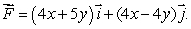 Let
Let 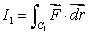 , where C1 is the line from (0, 0)to (2, 2).
, where C1 is the line from (0, 0)to (2, 2).Let
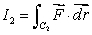 , where C2 is parameterized by
, where C2 is parameterized by 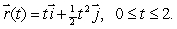 Notice that both C1 and C2 go from (0, 0)to (2, 2), but is
Notice that both C1 and C2 go from (0, 0)to (2, 2), but is 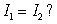 Explain.
Explain.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
35
Let C be the curve x = 2t + cos t, y = 4t, z = 2 sin t for 0 t 3 /2.
Use a potential function to evaluate exactly, where
Use a potential function to evaluate exactly, where

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
36
Let 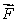 be a conservative vector field with potential function g satisfying g(0, 0)= -5.Let C1 be the line from (0, 0)to (2, 1), C2 the path parameterized by
be a conservative vector field with potential function g satisfying g(0, 0)= -5.Let C1 be the line from (0, 0)to (2, 1), C2 the path parameterized by 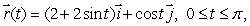 and C3 the path parameterized by
and C3 the path parameterized by 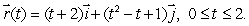 Suppose that
Suppose that 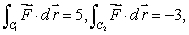 and
and 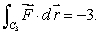 Evaluate g(2, -1).
Evaluate g(2, -1).
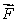 be a conservative vector field with potential function g satisfying g(0, 0)= -5.Let C1 be the line from (0, 0)to (2, 1), C2 the path parameterized by
be a conservative vector field with potential function g satisfying g(0, 0)= -5.Let C1 be the line from (0, 0)to (2, 1), C2 the path parameterized by 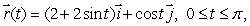 and C3 the path parameterized by
and C3 the path parameterized by 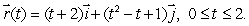 Suppose that
Suppose that 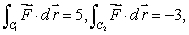 and
and 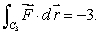 Evaluate g(2, -1).
Evaluate g(2, -1).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the two-dimensional vector field 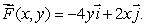 Write down parameterizations of the three line segments C1, C2, and C3 shown in the figure below.
Write down parameterizations of the three line segments C1, C2, and C3 shown in the figure below. 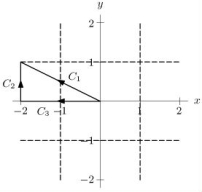 Use your parameterizations to compute the line integral
Use your parameterizations to compute the line integral 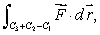 by finding
by finding 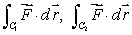 and
and 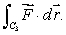
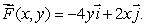 Write down parameterizations of the three line segments C1, C2, and C3 shown in the figure below.
Write down parameterizations of the three line segments C1, C2, and C3 shown in the figure below.  Use your parameterizations to compute the line integral
Use your parameterizations to compute the line integral 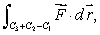 by finding
by finding 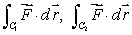 and
and 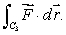

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
38
Explain what is meant by saying a vector field is conservative.
A)A vector field is called conservative if for any two points P and Q, the line integral
has the same value along any path C from P to Q lying in the domain of
B)A vector field is called conservative if for any two points P and Q, the line integral
has a different value along any path C from P to Q lying in the domain of
C)A vector field is called conservative if for any two points P and Q, the line integral
has the same value along a path C from P to Q lying in the domain of
D)A vector field is called conservative if for two specific points P and Q, the line integral
has the same value along any path C from P to Q lying in the domain of
A)A vector field is called conservative if for any two points P and Q, the line integral
has the same value along any path C from P to Q lying in the domain of
B)A vector field is called conservative if for any two points P and Q, the line integral
has a different value along any path C from P to Q lying in the domain of
C)A vector field is called conservative if for any two points P and Q, the line integral
has the same value along a path C from P to Q lying in the domain of
D)A vector field is called conservative if for two specific points P and Q, the line integral
has the same value along any path C from P to Q lying in the domain of

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the vector field 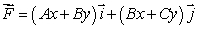 for certain constants A, B and C.
for certain constants A, B and C.
Show that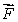 is path-independent by finding its potential function.
is path-independent by finding its potential function.
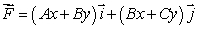 for certain constants A, B and C.
for certain constants A, B and C.Show that
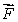 is path-independent by finding its potential function.
is path-independent by finding its potential function.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
40
Let C be the circle in space with the parameterization 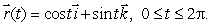 Evaluate
Evaluate 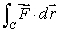 where
where 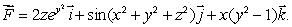
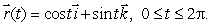 Evaluate
Evaluate 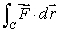 where
where 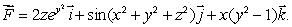

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
41
Let 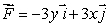 and let Ca be the circle x2 + y2 = a2 traversed counterclockwise.
and let Ca be the circle x2 + y2 = a2 traversed counterclockwise.
Find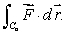
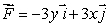 and let Ca be the circle x2 + y2 = a2 traversed counterclockwise.
and let Ca be the circle x2 + y2 = a2 traversed counterclockwise.Find
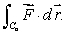

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
42
The following table gives values of a function f(x, y).The table reflects the properties of the function, which is differentiable and defined for all (x, y). 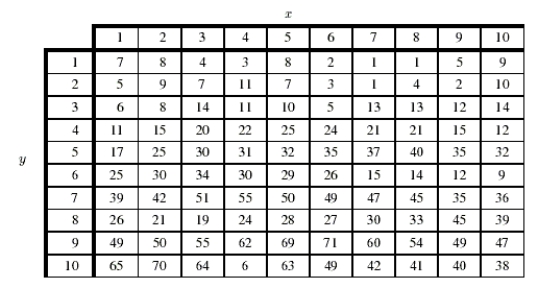 Let
Let 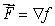 and
and 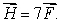 Find
Find 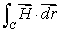 if C is the circle of radius 2 centered at (4, 3).
if C is the circle of radius 2 centered at (4, 3).
 Let
Let 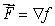 and
and 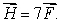 Find
Find 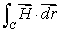 if C is the circle of radius 2 centered at (4, 3).
if C is the circle of radius 2 centered at (4, 3).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
43
Let 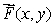 be the vector field
be the vector field 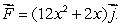 Find
Find 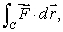 using Green's theorem, if C is the unit circle traveled counterclockwise.
using Green's theorem, if C is the unit circle traveled counterclockwise.
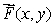 be the vector field
be the vector field 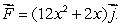 Find
Find 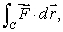 using Green's theorem, if C is the unit circle traveled counterclockwise.
using Green's theorem, if C is the unit circle traveled counterclockwise.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
44
Use Green's Theorem to calculate the circulation of 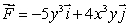 around the triangle with vertices (0, 0), (1, 0)and (0, 1), oriented counter-clockwise.
around the triangle with vertices (0, 0), (1, 0)and (0, 1), oriented counter-clockwise.
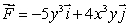 around the triangle with vertices (0, 0), (1, 0)and (0, 1), oriented counter-clockwise.
around the triangle with vertices (0, 0), (1, 0)and (0, 1), oriented counter-clockwise.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
45
If C1 and C2 are two curves with the same starting and ending points, then , for any vector field

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
46
If is a path-independent field, then where C has the parameterization

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
47
Let 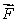 and
and 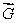 be two 2-dimensional fields, where
be two 2-dimensional fields, where 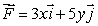 and
and 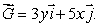 Let C1 be the circle with center (2, 2)and radius 1 oriented counterclockwise.
Let C1 be the circle with center (2, 2)and radius 1 oriented counterclockwise.
Let C2 be the path consisting of the straight line segments from (0, 4)to (0, 1)and from (0, 1)to (3, 1).
Find the line integral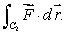 Use "pi" to represent
Use "pi" to represent  if necessary.
if necessary.
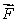 and
and 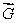 be two 2-dimensional fields, where
be two 2-dimensional fields, where 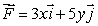 and
and 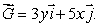 Let C1 be the circle with center (2, 2)and radius 1 oriented counterclockwise.
Let C1 be the circle with center (2, 2)and radius 1 oriented counterclockwise.Let C2 be the path consisting of the straight line segments from (0, 4)to (0, 1)and from (0, 1)to (3, 1).
Find the line integral
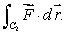 Use "pi" to represent
Use "pi" to represent 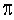 if necessary.
if necessary.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
48
Let be the vector field shown below. 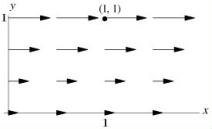 Let C be the rectangular loop from (0, 0)to (1, 0)to (1, 1)to (0, 1), then back to (0, 0). Do you expect the line integral to be positive, negative or zero?
Let C be the rectangular loop from (0, 0)to (1, 0)to (1, 1)to (0, 1), then back to (0, 0). Do you expect the line integral to be positive, negative or zero?
A)Positive
B)Negative
 Let C be the rectangular loop from (0, 0)to (1, 0)to (1, 1)to (0, 1), then back to (0, 0). Do you expect the line integral to be positive, negative or zero?
Let C be the rectangular loop from (0, 0)to (1, 0)to (1, 1)to (0, 1), then back to (0, 0). Do you expect the line integral to be positive, negative or zero?A)Positive
B)Negative

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
49
Which of the two vector fields shown below is not conservative?
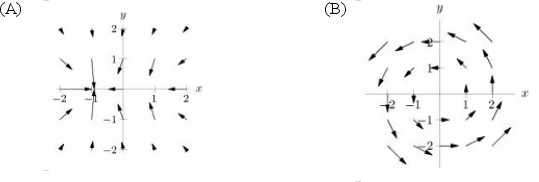


Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
50
Use Green's Theorem to evaluate 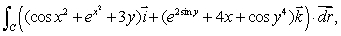 where C is the circle of radius
where C is the circle of radius 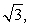 centered at
centered at 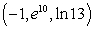 oriented in a counter-clockwise direction.
oriented in a counter-clockwise direction.
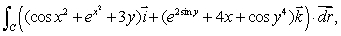 where C is the circle of radius
where C is the circle of radius 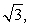 centered at
centered at 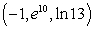 oriented in a counter-clockwise direction.
oriented in a counter-clockwise direction.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
51
Let 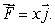 Let C1 be the line from (0, 0)to (2, 0), C2 the line from (2, 0)to (2,-1), C3 the line from (2,-1)to (0,-1), and C4 the line from (0,-1)to (0, 0).
Let C1 be the line from (0, 0)to (2, 0), C2 the line from (2, 0)to (2,-1), C3 the line from (2,-1)to (0,-1), and C4 the line from (0,-1)to (0, 0).
(A)Using the definition of line integral only, without parameterizing the curves, show that the line integral of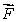 along C = C1 + C2 + C3 + C4 is -2.That is, show
along C = C1 + C2 + C3 + C4 is -2.That is, show 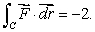 (B)The rectangle, R, enclosed by the lines C1, C2, C3 and C4 is of area 2.So, by Green's Theorem
(B)The rectangle, R, enclosed by the lines C1, C2, C3 and C4 is of area 2.So, by Green's Theorem 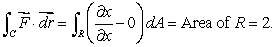 Is something wrong?
Is something wrong?
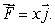 Let C1 be the line from (0, 0)to (2, 0), C2 the line from (2, 0)to (2,-1), C3 the line from (2,-1)to (0,-1), and C4 the line from (0,-1)to (0, 0).
Let C1 be the line from (0, 0)to (2, 0), C2 the line from (2, 0)to (2,-1), C3 the line from (2,-1)to (0,-1), and C4 the line from (0,-1)to (0, 0).(A)Using the definition of line integral only, without parameterizing the curves, show that the line integral of
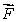 along C = C1 + C2 + C3 + C4 is -2.That is, show
along C = C1 + C2 + C3 + C4 is -2.That is, show 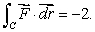 (B)The rectangle, R, enclosed by the lines C1, C2, C3 and C4 is of area 2.So, by Green's Theorem
(B)The rectangle, R, enclosed by the lines C1, C2, C3 and C4 is of area 2.So, by Green's Theorem 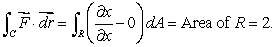 Is something wrong?
Is something wrong?
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
52
Let 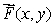 be the vector field
be the vector field 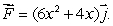 Find
Find 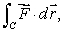 where C is the line from (0, 0)to (4, 4).
where C is the line from (0, 0)to (4, 4).
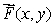 be the vector field
be the vector field 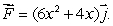 Find
Find 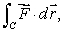 where C is the line from (0, 0)to (4, 4).
where C is the line from (0, 0)to (4, 4).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
53
Find the line integral of 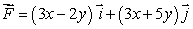 around the curve consisting of the graph of y = xn from the origin to the point (1, 1), followed by straight lines from (1, 1)to (0, 1)and from (0, 1)back to the origin.
around the curve consisting of the graph of y = xn from the origin to the point (1, 1), followed by straight lines from (1, 1)to (0, 1)and from (0, 1)back to the origin.
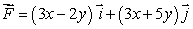 around the curve consisting of the graph of y = xn from the origin to the point (1, 1), followed by straight lines from (1, 1)to (0, 1)and from (0, 1)back to the origin.
around the curve consisting of the graph of y = xn from the origin to the point (1, 1), followed by straight lines from (1, 1)to (0, 1)and from (0, 1)back to the origin.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
54
Is the following vector field is a gradient vector field?
A)Yes
B)No
A)Yes
B)No

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
55
Let C be the circular path which is the portion of the circle of radius 1 centered at the origin starting at (1, 0)and ending at (0,-1), oriented counterclockwise.
Let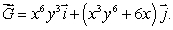 Determine the exact value of
Determine the exact value of 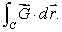
Let
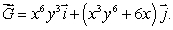 Determine the exact value of
Determine the exact value of 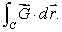

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
56
Let 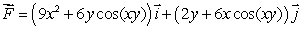 .
.
Calculate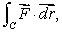 where C is the curve shown below.
where C is the curve shown below. 
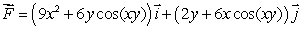 .
.Calculate
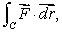 where C is the curve shown below.
where C is the curve shown below. 

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
57
The following table gives values of a function f(x, y).The table reflects the properties of the function, which is differentiable and defined for all (x, y). 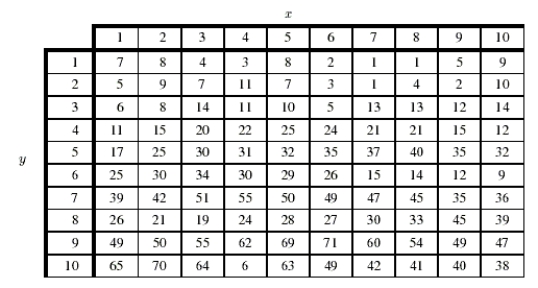 Let
Let 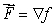 and
and 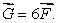 Find
Find 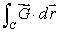 if C consists of line segments connecting (1,1), (1,10), (5,6), and (9,8)in that order.Explain your reasoning.
if C consists of line segments connecting (1,1), (1,10), (5,6), and (9,8)in that order.Explain your reasoning.
 Let
Let 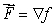 and
and 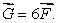 Find
Find 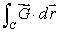 if C consists of line segments connecting (1,1), (1,10), (5,6), and (9,8)in that order.Explain your reasoning.
if C consists of line segments connecting (1,1), (1,10), (5,6), and (9,8)in that order.Explain your reasoning.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
58
Let 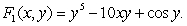 Find a function
Find a function 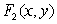 , such that
, such that 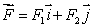 is a gradient field.
is a gradient field.
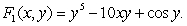 Find a function
Find a function 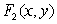 , such that
, such that 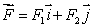 is a gradient field.
is a gradient field.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
59
Use Green's Theorem to find the line integral of 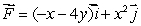 around the closed curve composed of the graph of y = x2n where n is a positive integer and the line y = 1.
around the closed curve composed of the graph of y = x2n where n is a positive integer and the line y = 1.
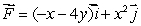 around the closed curve composed of the graph of y = x2n where n is a positive integer and the line y = 1.
around the closed curve composed of the graph of y = x2n where n is a positive integer and the line y = 1.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
60
Let 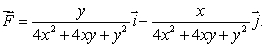 Check that
Check that 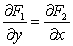 .Is
.Is 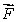 is path-independent?
is path-independent?
 Check that
Check that 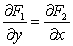 .Is
.Is 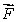 is path-independent?
is path-independent?
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
61
On an exam, students were asked to evaluate 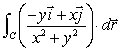 , where C is the circle centered at the origin of radius r:
, where C is the circle centered at the origin of radius r: 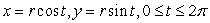 .One student wrote:
.One student wrote:
"Since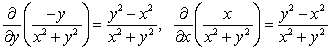 Using Green's Theorem,
Using Green's Theorem, 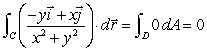 ."
."
Do you agree with the student?
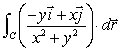 , where C is the circle centered at the origin of radius r:
, where C is the circle centered at the origin of radius r: 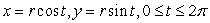 .One student wrote:
.One student wrote:"Since
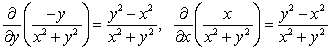 Using Green's Theorem,
Using Green's Theorem, 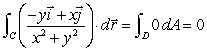 ."
."Do you agree with the student?

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
62
Let (a)Find the line integral , where C1 is the line from (0, 0)to ( , 0).
(b)Evaluate the double integral where R is the region enclosed by the curve y = sin x and the x-axis for 0 x .What is the geometric meaning of this integral?
(c)Use Green's Theorem and the result of part (a)to find where C2 is the path from (0, 0)to ( , 0)along the curve y = sin x.
(b)Evaluate the double integral where R is the region enclosed by the curve y = sin x and the x-axis for 0 x .What is the geometric meaning of this integral?
(c)Use Green's Theorem and the result of part (a)to find where C2 is the path from (0, 0)to ( , 0)along the curve y = sin x.

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
63
Calculate the line integral of 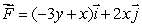 along the straight line from (3, -3)to (3, 0).
along the straight line from (3, -3)to (3, 0).
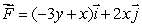 along the straight line from (3, -3)to (3, 0).
along the straight line from (3, -3)to (3, 0).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
64
Let Use the curl test to check whether is path-independent.
A)Path-independent
B)Not path-independent
A)Path-independent
B)Not path-independent

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
65
Let Is the value of the line integral of along any loop zero?
A)Yes; the function is a gradient vector field.
B)No; the function is not a gradient vector field.
A)Yes; the function is a gradient vector field.
B)No; the function is not a gradient vector field.

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
66
Let For a fixed , let C be the line segment from (0, 0)to the point (cos , sin )on the unit circle.
Find a parameterization of C and compute .(Your answer will depend on .)
Find a parameterization of C and compute .(Your answer will depend on .)

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
67
On an exam, students were asked to evaluate 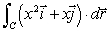 , where C has the parameterization
, where C has the parameterization 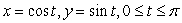 .One student wrote:
.One student wrote:
"Using Green's Theorem,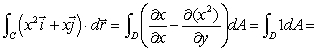 Area of the semi-circle =
Area of the semi-circle = 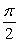 ."
."
Do you agree with the student?
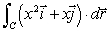 , where C has the parameterization
, where C has the parameterization 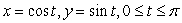 .One student wrote:
.One student wrote:"Using Green's Theorem,
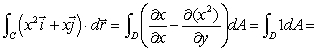 Area of the semi-circle =
Area of the semi-circle = 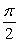 ."
."Do you agree with the student?

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
68
Let 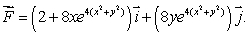 Find a potential function for
Find a potential function for 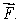
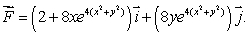 Find a potential function for
Find a potential function for 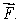

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
69
Suppose a curve C is parameterized by 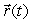 with
with 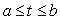 and suppose
and suppose 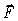 is a vector field
is a vector field 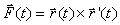 for
for 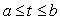 .Explain why
.Explain why 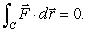
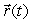 with
with 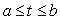 and suppose
and suppose 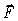 is a vector field
is a vector field 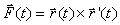 for
for 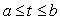 .Explain why
.Explain why 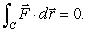

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
70
Let C be the unit circle oriented in a counter-clockwise direction.Say whether the following statements are true or false.If , we can conclude that is not path-independent field.

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
71
Let 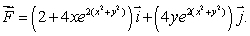 Find the value of
Find the value of 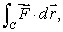 where C is a path joining (0, 0)to the point (1, 2).
where C is a path joining (0, 0)to the point (1, 2).
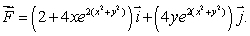 Find the value of
Find the value of 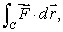 where C is a path joining (0, 0)to the point (1, 2).
where C is a path joining (0, 0)to the point (1, 2).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
72
State the Fundamental Theorem of Calculus for Line Integrals.
A)Suppose C is a piece-wise smooth oriented path with starting point P and end point Q.Then
B)Suppose C is a oriented path with starting point P and end point Q.Then
C)Suppose C is a piece-wise smooth oriented path with starting point P and end point Q.If f is a function whose gradient is continuous on the path C, then
D)Suppose C is a piece-wise smooth oriented path with starting point P and end point Q.If f is a function whose gradient is continuous on the path C, then
A)Suppose C is a piece-wise smooth oriented path with starting point P and end point Q.Then
B)Suppose C is a oriented path with starting point P and end point Q.Then
C)Suppose C is a piece-wise smooth oriented path with starting point P and end point Q.If f is a function whose gradient is continuous on the path C, then
D)Suppose C is a piece-wise smooth oriented path with starting point P and end point Q.If f is a function whose gradient is continuous on the path C, then

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
73
Let Ca be the circle x2 + y2 = a2 oriented counter-clockwise.
Use Green's theorem to find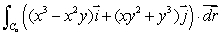
Use Green's theorem to find
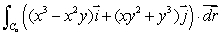

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
74
Calculate the line integral of 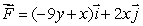 along a quarter of a circle centered at the origin, starting at (3, 0)and ending at (0, -3).
along a quarter of a circle centered at the origin, starting at (3, 0)and ending at (0, -3).
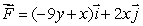 along a quarter of a circle centered at the origin, starting at (3, 0)and ending at (0, -3).
along a quarter of a circle centered at the origin, starting at (3, 0)and ending at (0, -3).
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
75
Let f(x, y, z)be a function of three variables.Suppose that C is an oriented curve lying on the level surface f(x, y, z)= 2.
Find the line integral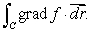
Find the line integral
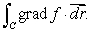

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
76
Let 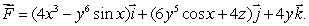 Show that
Show that 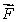 is a gradient field by finding its potential function.
is a gradient field by finding its potential function.
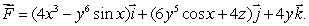 Show that
Show that 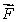 is a gradient field by finding its potential function.
is a gradient field by finding its potential function.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
77
Answer true or false, giving a reason for your answer.Let 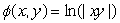 so that
so that 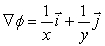 .
.
Then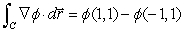 where C is given by the parametrization
where C is given by the parametrization 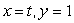 for
for 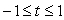 .
.
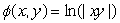 so that
so that 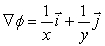 .
.Then
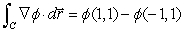 where C is given by the parametrization
where C is given by the parametrization 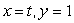 for
for 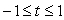 .
.
Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck
78
Let C be the unit circle oriented in a counter-clockwise direction.Say whether the following statements are true or false.
If , we can conclude that is path-independent field.
If , we can conclude that is path-independent field.

Unlock Deck
Unlock for access to all 78 flashcards in this deck.
Unlock Deck
k this deck


