Exam 18: Line Integrals

Consider the two-dimensional vector field $\vec { F } ( x , y ) = - 4 y \vec { i } + 2 x \vec { j }$ Write down parameterizations of the three line segments C₁, C₂, and C₃ shown in the figure below. 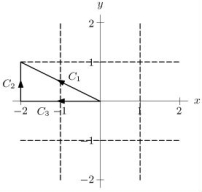Use your parameterizations to compute the line integral $\int _ { C _ { 3 } + C _ { 2 } - C _ { 1 } } \vec { F } \cdot d \vec { r }$ by finding $\int_{G_{1}} \vec{F} \cdot d \vec{r}, \int_{C_{2}} \vec{F} \cdot d \vec{r}$ and $\int _ { C _ { 3 } } \vec { F } \cdot d \vec { r }$

Find, by direct computation, the line integral of $y \vec { i } - x \vec { j }$ around the circle $\vec { r } ( t ) = \cos t \vec { i } + \sin t \vec { j } , 0 \leq t \leq 2 \pi$

Let C be the curve described by $\vec { r } ( t )$ .If the angle between $\vec { F } ( t )$ and $\vec { r } ^ { \prime } ( t )$ is less than $\pi$ /2, then $\int _ { C } \vec { F } \cdot \overline { d r } \geq 0$

The following table gives values of a function f(x, y).The table reflects the properties of the function, which is differentiable and defined for all (x, y). x y 1 2 3 4 5 6 7 8 9 10 1 7 8 4 3 8 2 1 1 5 9 2 5 9 7 11 7 3 1 4 2 10 3 6 8 14 11 10 5 13 13 12 14 4 11 15 20 22 25 24 21 21 15 12 5 17 25 30 31 32 35 37 40 35 32 6 25 30 34 30 29 26 15 14 12 9 7 39 42 51 55 50 49 47 45 35 36 8 26 21 19 24 28 27 30 33 45 39 9 49 50 55 62 69 71 60 54 49 47 10 65 70 64 6 63 49 42 41 40 38 Let $\vec{F}=\nabla f$ and $\vec { G } = 6 \overline { \bar { F } } .$ Find $\int _ { C } \vec { G } \cdot d \vec { r }$ if C consists of line segments connecting (1,1), (1,10), (5,6), and (9,8)in that order.Explain your reasoning.

Let $\vec{F}=-3 y \vec{i}+3 x \vec{j}$ and let C_a be the circle x² + y² = a² traversed counterclockwise. Find $\int _ { c _ { 0 } } \vec { F } \cdot d \vec { r }$

Let $\vec { F } = \left( 9 x ^ { 2 } + 6 y \cos ( x y ) \right) \vec { i } + ( 2 y + 6 x \cos ( x y ) ) \vec { j }$ . Calculate $\int_{C} \overline{\vec{F}} \cdot \overline{d r}$ where C is the curve shown below.

Let $\vec { F } = x ^ { 3 } \vec { i } + \left( x + \sin ^ { 3 } y \right) \vec { j }$ (a)Find the line integral $\int _ { C _ { 1 } } \vec { F } \cdot d \vec { r }$ , where C₁ is the line from (0, 0)to ( $\pi$ , 0). (b)Evaluate the double integral $\int _ { R } 1 d A$ where R is the region enclosed by the curve y = sin x and the x-axis for 0 $\le$ x $\le$ $\pi$ .What is the geometric meaning of this integral? (c)Use Green's Theorem and the result of part (a)to find $\int _ { c _ { 2 } } \vec { F } \cdot d \vec { r }$ where C₂ is the path from (0, 0)to ( $\pi$ , 0)along the curve y = sin x.

Consider the vector field $\vec { F } = ( A x + B y ) \vec { i } + ( B x + C y ) \vec { j }$ for certain constants A, B and C. Find the line integral $\int _ { C _ { 1 } } \vec { F } \cdot d \vec { r }$ , where C₁ is the curve $x = e ^ { t ( t - 2 ) } + 6 t , y = \sin \left( \frac { \pi } { 4 } t \right) , 0 \leq t \leq 2$

Find $\int_{C} \vec{F} \cdot d \vec{r}$ where $\vec{F}=(x+z) \vec{i}+6 z \vec{j}+6 y \vec{k}$ and C is the line from the point (2, 4, 4)to the point (0, 6, -8).

Evaluate $\int _ { - c } - 2 x \vec { i } + ( 4 x + y ) \vec { j }$ , where C is the triangular path from (0, 0)to (1, 1)to (0, 1)to (0, 0).

Let $\vec{F}$ be a conservative vector field with potential function g satisfying g(0, 0)= -5.Let C₁ be the line from (0, 0)to (2, 1), C₂ the path parameterized by $\vec { r } ( t ) = ( 2 + 2 \sin t ) \vec { i } + \cos t \vec { j } , \quad 0 \leq t \leq \pi$ and C₃ the path parameterized by $\vec { r } ( t ) = ( t + 2 ) \vec { i } + \left( t ^ { 2 } - t + 1 \right) \vec { j } , 0 \leq t \leq 2$ Suppose that $\int _ { C _ { 1 } } \vec { F } \cdot d \vec { r } = 5 , \int _ { C _ { 2 } } \vec { F } \cdot d \vec { r } = - 3$ and $\int _ { C _ { 3 } } \vec { F } \cdot d \vec { r } = - 3$ Evaluate g(2, -1).

Let C be the circle in space with the parameterization $\vec { r } ( t ) = \cos t \vec { i } + \sin t \vec { k } , \quad 0 \leq t \leq 2 \pi$ Evaluate $\int_{C} \vec{F} \cdot d \vec{r}$ where $\vec { F } = 2 z e ^ { y ^ { 2 } } \vec { i } + \sin \left( x ^ { 2 } + y ^ { 2 } + z ^ { 2 } \right) \vec { j } + x \left( y ^ { 2 } - 1 \right) \vec { k }$

Let $\vec { F } = \left( 2 + 8 x e ^ { 4 \left( x ^ { 2 } + y ^ { 2 } \right) } \right) \vec { i } + \left( 8 y e ^ { 4 \left( x ^ { 2 } + y ^ { 2 } \right) } \right) \vec { j }$ Find a potential function for $\vec{F}$

Let $\vec { F } ( x , y )$ be the vector field $\vec{F}=\left(12 x^{2}+2 x\right) \vec{j}$ Find $\int _ { C } \vec { F } \cdot d \vec { r }$ using Green's theorem, if C is the unit circle traveled counterclockwise.

Let $\vec { F } ( x , y )$ be the vector field $\vec{F}=\left(6 x^{2}+4 x\right) \vec{j}$ Find $\int _ { C } \vec { F } \cdot d \vec { r }$ where C is the line from (0, 0)to (4, 4).

Consider the vector field $\vec { F } = ( A x + B y ) \vec { i } + ( B x + C y ) \vec { j }$ for certain constants A, B and C. Use the definition of the line integral to evaluate $\int_{C} \vec{F} \cdot d \vec{r}$ , where C is the line from (1, 0)to (11, 1).

Calculate the line integral of $\vec{F}=(-3 y+x) \vec{i}+2 x \vec{j}$ along the straight line from (3, -3)to (3, 0).

Let $\vec{F}=\left(3 x^{2}+y^{4} \sin x\right) \vec{i}+\left(4 y^{3} \cos x+z\right) \vec{j}-y \vec{k}$ Is the value of the line integral of $\vec{F}$ along any loop zero?

Let $\vec{F}=\operatorname{grad} f$ , where $f ( x , y ) = \ln \left( 2 x ^ { 2 } + 3 y ^ { 2 } + 1 \right)$ (a)Evaluate the line integral $\int _ { C } \vec { F } \cdot \overline { d r }$ , where C is the line from (0, 0)to (2, -4). (b)Do you expect the line integral of $\vec{F}$ along the parabola y = x²-4x, 0 $\le$ x $\le$ 2 to equal to the answer to (a)?

Let $\vec{F}=\left(4 x^{3}-y^{6} \sin x\right) \vec{i}+\left(6 y^{5} \cos x+4 z\right) \vec{j}+4 y \vec{k}$ Show that $\vec{F}$ is a gradient field by finding its potential function.