Deck 17: Parameterization and Vector Fields
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/86
Play
Full screen (f)
Deck 17: Parameterization and Vector Fields
1
Find parametric equations for the line through the point (1, 5, 2)and parallel to the vector 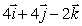 in which the particle is moving with speed 24 (the parameter t represents time).
in which the particle is moving with speed 24 (the parameter t represents time).
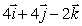 in which the particle is moving with speed 24 (the parameter t represents time).
in which the particle is moving with speed 24 (the parameter t represents time).x = 1 + 16 t, y = 5 + 16 t, and z = 2 - 8 t.
2
Let f(x, y, z)= xy + 6yz + zx.Then f(2, 2, 3)= 46.
Give an equation to the tangent plane to xy + 6yz + zx = 46.
Give an equation to the tangent plane to xy + 6yz + zx = 46.
5x + 20y + 14z = 92
3
Find a parametric equation for the line which passes through the point (5, 1, -1)and is parallel to the line 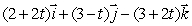 .
.
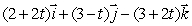 .
.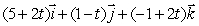
4
Which of the following equations give alternate parameterizations of the line L parameterized by
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
5
Write down a parameterization of the line through the points (2, 2, 4)and (6, 4, 2).Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the plane x - 4y + 4z = 5 and the line x = a + bt, y = 2 + 2t, z = 5 - t.
Find the values of a and b such that the line lies in the plane.
Find the values of a and b such that the line lies in the plane.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
7
Describe the similarities and differences between the following two curves.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
8
Find a parameterization of a curve that looks like sin y = z when viewed from the x-axis, and looks like x = z2 when viewed from the y-axis.See the shadows drawn on the planes in the following picture. 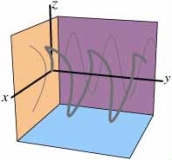 What does the curve look like when viewed from the z-axis?
What does the curve look like when viewed from the z-axis?
 What does the curve look like when viewed from the z-axis?
What does the curve look like when viewed from the z-axis?
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
9
Find a parameterization for the circle of radius 4 in the xz-plane, centered at the point (3, 0, -5).Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
10
What curve, C, is traced out by the parameterization for 0 t 2 ?
Either give a very complete verbal description or sketch the curve (or both).
Either give a very complete verbal description or sketch the curve (or both).

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
11
The line through the points (2, 5, 25)and (12, 7, 23)can be parameterized by 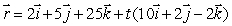 .
.
What value of t gives the point (42, 13, 17)?
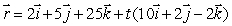 .
.What value of t gives the point (42, 13, 17)?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
12
Give parameterizations for a circle of radius 2 in the plane, centered at origin, traversed anticlockwise.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
13
Find a parameterization for the curve y6 = x7 in the xy-plane.Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose z = f(x, y), f(1, 3)= 5 and the vector is perpendicular to the graph of f(x, y)at the point (1, 3).

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
15
The equation 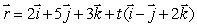 parameterizes a line through the point (4, 3, 7).
parameterizes a line through the point (4, 3, 7).
What is the value of t at this point?
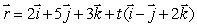 parameterizes a line through the point (4, 3, 7).
parameterizes a line through the point (4, 3, 7).What is the value of t at this point?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the plane x - 4y + -2z = 5 and the line x = a + bt, y = 2 + -2t, z = 2 - t.
Find the value of b such that the line is perpendicular to the plane.
Find the value of b such that the line is perpendicular to the plane.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
17
Find parametric equations for a line through the points, A = (-2, 5, 4)and B = (-2, 25, 9)so that the point A corresponds to t = 0 and the point B to t = 5.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the plane 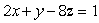 and the line with parametric equation
and the line with parametric equation 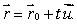 Give a value of
Give a value of 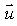 which makes the line parallel to the plane.(There are many possible answers.)
which makes the line parallel to the plane.(There are many possible answers.)
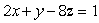 and the line with parametric equation
and the line with parametric equation 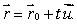 Give a value of
Give a value of 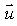 which makes the line parallel to the plane.(There are many possible answers.)
which makes the line parallel to the plane.(There are many possible answers.)
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
19
Give parameterizations for a circle of radius 3 in 3-space perpendicular to the y-axis centered at (4, -2, 0).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
20
A child is sliding down a helical slide.Her position at time t after the start is given in feet by .The ground is the xy-plane.
At time t = 2 , the child leaves the slide on the tangent to the slide at that point.What is the equation of the tangent line?
At time t = 2 , the child leaves the slide on the tangent to the slide at that point.What is the equation of the tangent line?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
21
Write a formula for a vector field 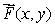 whose vectors are parallel to the x-axis and point away from the y-axis, with magnitude inversely proportional to the cube of the distance from the x-axis.
whose vectors are parallel to the x-axis and point away from the y-axis, with magnitude inversely proportional to the cube of the distance from the x-axis.
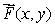 whose vectors are parallel to the x-axis and point away from the y-axis, with magnitude inversely proportional to the cube of the distance from the x-axis.
whose vectors are parallel to the x-axis and point away from the y-axis, with magnitude inversely proportional to the cube of the distance from the x-axis.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
22
Find the coordinates of the point where the line tangent to the curve 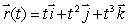 at the point (4, 16, 64)crosses the xy-plane.
at the point (4, 16, 64)crosses the xy-plane.
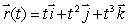 at the point (4, 16, 64)crosses the xy-plane.
at the point (4, 16, 64)crosses the xy-plane.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
23
A particle moves at a constant speed along a line through P = (10,-20, 22)and Q = (22, -46, 46).Find a parametric equation for the line if the particle passes through P at time t = 3 and passes through Q at time t = 7.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
24
Calculate the length of the curve 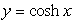 from x = -3 to x = 3.
from x = -3 to x = 3.
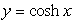 from x = -3 to x = 3.
from x = -3 to x = 3.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
25
A particle moves with position vector . Describe the movement of the particle as t .
A)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive y-axis with slower and slower speed.
B)The particle will approach the positive y-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive x-axis with slower and slower speed.
C)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive x-axis with increasing speed.
D)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive x-axis with slower and slower speed.
E)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive z-axis with slower and slower speed.
A)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive y-axis with slower and slower speed.
B)The particle will approach the positive y-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive x-axis with slower and slower speed.
C)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive x-axis with increasing speed.
D)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive x-axis with slower and slower speed.
E)The particle will approach the positive x-axis asymptotically as t .Also, since each component of approaches 0 as t , we expect the particle to approach the positive z-axis with slower and slower speed.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
26
The equation 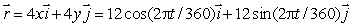 describes the motion of a particle moving on a circle.Assume x and y are in miles and t is in days.
describes the motion of a particle moving on a circle.Assume x and y are in miles and t is in days.
What is the speed of the particle when it passes through the point (0, 2)?
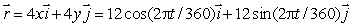 describes the motion of a particle moving on a circle.Assume x and y are in miles and t is in days.
describes the motion of a particle moving on a circle.Assume x and y are in miles and t is in days.What is the speed of the particle when it passes through the point (0, 2)?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
27
Let f(x, y)be a function that depends on only one of the variables, that is, of the form f(x, y)= g(x)or f(x, y)= g(y). Could the following picture be the gradient of f? 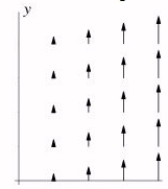
A)No
B)Yes
C)Not possible to say

A)No
B)Yes
C)Not possible to say

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
28
The parametric vector form of the position of a roller coaster is Answer the following questions about the ride.
(a)The scariest point of the ride is when it is traveling fastest.For which value of t > 0 does this occur first?
(b)Does the velocity vector of the roller coaster ever point directly downward?
(a)The scariest point of the ride is when it is traveling fastest.For which value of t > 0 does this occur first?
(b)Does the velocity vector of the roller coaster ever point directly downward?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
29
Match the vector field with the descriptions (a)-(d).
A)A swirling in a clockwise direction.
B)An attractive force field pointing toward the origin.
C)A repulsive force field pointing away from the origin.
D)A swirling in a counter-clockwise direction.
A)A swirling in a clockwise direction.
B)An attractive force field pointing toward the origin.
C)A repulsive force field pointing away from the origin.
D)A swirling in a counter-clockwise direction.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
30
A vector field 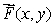 is shown below.
is shown below. 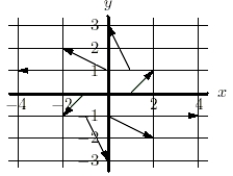 Find
Find 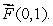
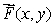 is shown below.
is shown below.  Find
Find 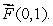

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
31
For the following vector field, identify which one of the following formulas could represent it. The scales in the x and y directions are the same.No reasons need be given. 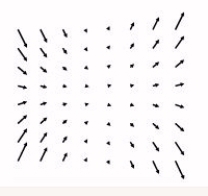
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
32
Answer the following as "true", "false" or "need more information".
If a particle moves with velocity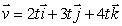 , then the particle stops at the origin.
, then the particle stops at the origin.
If a particle moves with velocity
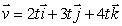 , then the particle stops at the origin.
, then the particle stops at the origin.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
33
The path of an object moving in xyz-space is given by 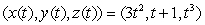 .
.
The temperature at a point (x, y, z)in space is given by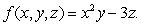 Calculate the directional derivative of f in the direction of
Calculate the directional derivative of f in the direction of 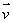 at the point (12, 3, 8), where
at the point (12, 3, 8), where 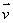 is the velocity vector of the object..
is the velocity vector of the object..
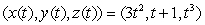 .
.The temperature at a point (x, y, z)in space is given by
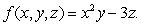 Calculate the directional derivative of f in the direction of
Calculate the directional derivative of f in the direction of 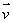 at the point (12, 3, 8), where
at the point (12, 3, 8), where 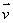 is the velocity vector of the object..
is the velocity vector of the object..
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
34
Find a parameterization of the curve 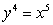 and use it to calculate the path length of this curve from (0, 0)to (1, 1).
and use it to calculate the path length of this curve from (0, 0)to (1, 1).
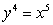 and use it to calculate the path length of this curve from (0, 0)to (1, 1).
and use it to calculate the path length of this curve from (0, 0)to (1, 1).
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
35
The path of an object moving in xyz-space is given by 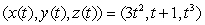 .
.
The temperature at a point (x, y, z)in space is given by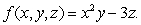 Calculate
Calculate 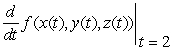 .
.
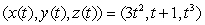 .
.The temperature at a point (x, y, z)in space is given by
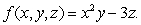 Calculate
Calculate 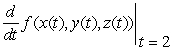 .
.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
36
Let 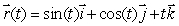 and let C be the helix parameterized by
and let C be the helix parameterized by 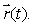 Find an expression for the outward pointing normal vector whose
Find an expression for the outward pointing normal vector whose 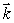 component is 0 at an arbitrary point ( sin(t), cos(t), t)of C.
component is 0 at an arbitrary point ( sin(t), cos(t), t)of C.
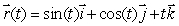 and let C be the helix parameterized by
and let C be the helix parameterized by 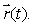 Find an expression for the outward pointing normal vector whose
Find an expression for the outward pointing normal vector whose 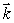 component is 0 at an arbitrary point ( sin(t), cos(t), t)of C.
component is 0 at an arbitrary point ( sin(t), cos(t), t)of C.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
37
Sketch the vector fields
A)
B)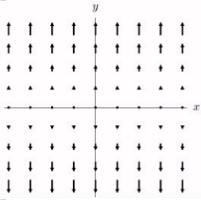
C)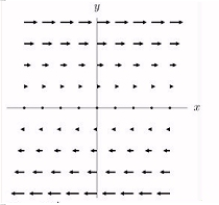
A)
B)

C)


Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
38
An object moves with constant velocity in 3-space.It passes through (4, 0, 1)at time t = 1 and through (13, 6, -11)at time t = 4.Find its velocity vector.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
39
The figure below shows the contour map of a function z = f(x, y). 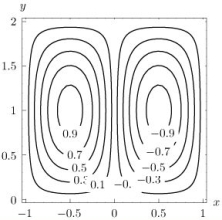 Let be the gradient vector field of f, i.e., Which of the vector fields show
Let be the gradient vector field of f, i.e., Which of the vector fields show
A)
B)
C)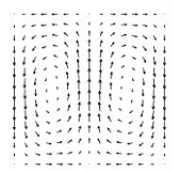
 Let be the gradient vector field of f, i.e., Which of the vector fields show
Let be the gradient vector field of f, i.e., Which of the vector fields show A)

B)

C)


Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
40
A particle moves at a constant speed along a line through P = (7,-14, 13)and Q = (19, -37, 37).Find a parametric equation for the line if:
The speed of the particle is 9 units per second and it is moving in the direction of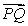 .
.
The speed of the particle is 9 units per second and it is moving in the direction of
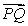 .
.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
41
Let 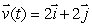 be a constant velocity field.
be a constant velocity field.
Find the flow line of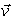 that passes through the origin at time t = 2.
that passes through the origin at time t = 2.
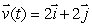 be a constant velocity field.
be a constant velocity field.Find the flow line of
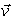 that passes through the origin at time t = 2.
that passes through the origin at time t = 2.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the plane Does it contain the point (-7, 8, -7)?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
43
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (5, 0, 4).
Let P be the plane containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
In each case, give a parameterization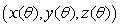 and specify the range of values your parameters must take on.
and specify the range of values your parameters must take on.
(i)the circle in which the cylinder, S, cuts the plane, P.
(ii)the surface of the cylinder S.
Let P be the plane containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
In each case, give a parameterization
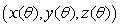 and specify the range of values your parameters must take on.
and specify the range of values your parameters must take on.(i)the circle in which the cylinder, S, cuts the plane, P.
(ii)the surface of the cylinder S.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
44
Let and Find a parametric equation for the plane through the point (1, 2, -1)and containing the vectors and Select all that apply.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose
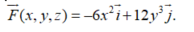
Find a function f(x, y, z) of three variables with the property that the vectors in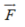 on a level surface of f (x, y, z) are perpendicular to the level surface of f(x, y, z) at each point.
on a level surface of f (x, y, z) are perpendicular to the level surface of f(x, y, z) at each point.
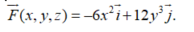
Find a function f(x, y, z) of three variables with the property that the vectors in
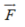 on a level surface of f (x, y, z) are perpendicular to the level surface of f(x, y, z) at each point.
on a level surface of f (x, y, z) are perpendicular to the level surface of f(x, y, z) at each point.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
46
Find the parametric equation of the plane through the point (5, 2, 2)and parallel to the lines and
Select all that apply.
A)
B)
C)
D)
E) .
Select all that apply.
A)
B)
C)
D)
E) .

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
47
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (5, 0, 4).
Find the xyz-equation of the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
Find the xyz-equation of the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
48
Match the surface with its parameterization below. 
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
49
Find parametric equations for the cylinder
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
50
Let 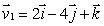 and
and 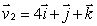 Find a vector which is perpendicular to
Find a vector which is perpendicular to 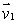 and
and 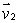 to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both
to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both 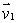 and
and 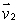 .Express your answer in the form
.Express your answer in the form 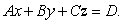
 and
and  Find a vector which is perpendicular to
Find a vector which is perpendicular to 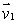 and
and 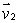 to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both
to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both 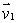 and
and 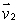 .Express your answer in the form
.Express your answer in the form 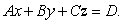

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
51
Find an equation for a vector field with all of the following properties.
• Defined at all points except (1, -5)
• All vectors have length 1.
• All vectors point away from the point (1, -5).
• Defined at all points except (1, -5)
• All vectors have length 1.
• All vectors point away from the point (1, -5).

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
52
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (2, 0, 7).
Find two unit vectors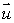 and
and 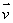 in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
Find two unit vectors
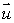 and
and 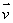 in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
in the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder)which are perpendicular to each other.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
53
The following equations represent a curve or a surface.Select the best geometric description. (Note: , , are spherical coordinates; r, , z are cylindrical coordinates.)
A)Part of a line through the origin
B)Part of a cylinder.
C)Part of a cone.
D)Disk
A)Part of a line through the origin
B)Part of a cylinder.
C)Part of a cone.
D)Disk

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
54
Find parametric equations for the cylinder
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
55
Using cylindrical coordinates, find parametric equations for the cylinder Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
56
Consider the parametric surface Does it contain the y-axis?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
57
The vector field 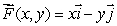 represents an ocean current.An iceberg is at the point (1, 2)at t = 0.
represents an ocean current.An iceberg is at the point (1, 2)at t = 0.
Determine the position of the iceberg at time t = 2.
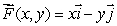 represents an ocean current.An iceberg is at the point (1, 2)at t = 0.
represents an ocean current.An iceberg is at the point (1, 2)at t = 0.Determine the position of the iceberg at time t = 2.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the parametric surface Does it contain the point (0, -3, -4)?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the plane Find a normal vector to the plane.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
60
Find parametric equations for the sphere 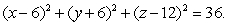
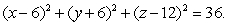

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
61
Consider the curve Does it pass through the point (1, -2, 0)?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
62
Parameterize the circle Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
63
Find the parametric equations for the line of the intersection of the planes 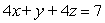 and
and 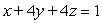 .
.
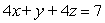 and
and 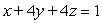 .
.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
64
Use cylindrical coordinates to parameterize the part of the plane x + y - z = 10 inside the cylinder .

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
65
If a particle is moving along a parameterized curve , then the acceleration vector at any point cannot be parallel to the velocity vector at that point.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
66
Are the lines parallel?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
67
The lines 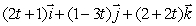 and
and 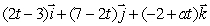 are perpendicular.Find a.
are perpendicular.Find a.
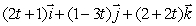 and
and 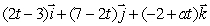 are perpendicular.Find a.
are perpendicular.Find a.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
68
Consider the curve Does the curve lie on the parametric surface

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
69
Let S be the parametric surface 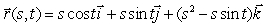 for
for 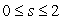 ,
, 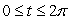 .
.
(a)What does the projection of S onto the xy-plane look like?
(b)Show that S is part of the surface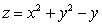 .
.
(c)Find a unit vector that is normal to the surface at the point (1,2,3).
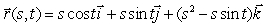 for
for 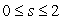 ,
, 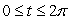 .
.(a)What does the projection of S onto the xy-plane look like?
(b)Show that S is part of the surface
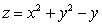 .
.(c)Find a unit vector that is normal to the surface at the point (1,2,3).

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
70
The curve 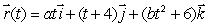 passes through the point (-12, 1, 51).Find a and b.
passes through the point (-12, 1, 51).Find a and b.
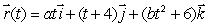 passes through the point (-12, 1, 51).Find a and b.
passes through the point (-12, 1, 51).Find a and b.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the curve 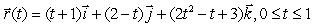 .
.
(a)Find a unit vector tangent to the curve at the point (1,2,3).
(b)Show that the curve lies on the surface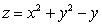 .
.
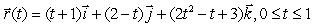 .
.(a)Find a unit vector tangent to the curve at the point (1,2,3).
(b)Show that the curve lies on the surface
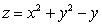 .
.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
72
Do the lines intersect?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
73
A surveyor wants to measure the height of a building.At point A = ( 733, -369, 0)on the ground, she observes that the vector 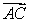 is parallel to
is parallel to 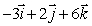 , where C is the highest point of the building.At point B = (418, 471, 0)she observes that the vector
, where C is the highest point of the building.At point B = (418, 471, 0)she observes that the vector 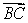 is parallel to
is parallel to 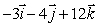 .Given that ground level is the plane z = 0 and the units are feet, find the height of the building.
.Given that ground level is the plane z = 0 and the units are feet, find the height of the building.
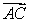 is parallel to
is parallel to 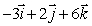 , where C is the highest point of the building.At point B = (418, 471, 0)she observes that the vector
, where C is the highest point of the building.At point B = (418, 471, 0)she observes that the vector 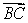 is parallel to
is parallel to 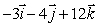 .Given that ground level is the plane z = 0 and the units are feet, find the height of the building.
.Given that ground level is the plane z = 0 and the units are feet, find the height of the building.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
74
If a particle moves with constant speed, the path of the particle must be a line.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
75
Parameterize the curve which lies on the plane 5x - 10y + z = 6 above the circle
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the curve 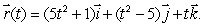 Find the equation of the tangent line at the point where t = 2.
Find the equation of the tangent line at the point where t = 2.
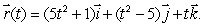 Find the equation of the tangent line at the point where t = 2.
Find the equation of the tangent line at the point where t = 2.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
77
Use spherical coordinates to parameterize the part of the sphere above the plane z = 1.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
78
The two planes are parallel.
Plane 1:
Plane 2:
Plane 1:
Plane 2:

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose the vector field represents an ocean current and that is a flow line of Find the acceleration vector of the flow line at (0, 9 /2).

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
80
How many parameters are needed to parameterize a surface in 3-space?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck


