Exam 17: Parameterization and Vector Fields

An object moves with constant velocity in 3-space.It passes through (4, 0, 1)at time t = 1 and through (13, 6, -11)at time t = 4.Find its velocity vector.

Write down a parameterization of the line through the points (2, 2, 4)and (6, 4, 2).Select all that apply.

Are the lines parallel? $l _ { 1 } : x = 2 t + 5 , y = 3 t + 3 , z = - 4 t - 2$ $l _ { 2 } : x = 5 t + 1 , y = 2 t - 4 , z = 11 t + 7$

Match the surface with its parameterization below.

If a particle moves with constant speed, the path of the particle must be a line.

Find parametric equations for the cylinder $49 x ^ { 2 } + 11 y ^ { 2 } = 539 , - 7 \leq z \leq 11$

Two particles p₁ and p₂ are moving in the plane, with p₁ moving vertically upward from initial point (0,0)and p₂ moving around the unit circle $x ^ { 2 } + y ^ { 2 } = 1$ with initial point (0, 1)in the counter-clockwise direction. (a)Choose parameterizations for p₁ and p₂ so that the two particles collide at the point of intersection of their paths. (b)If the sum of the speeds of these two particles is greater than 3 at the time of collision, then the two particles combine to become one.Will this happen with your chosen parameterization?

Let $\vec { v } _ { 1 } = 2 \vec { i } - 4 \vec { j } + \vec { k }$ and $\vec { v } _ { 2 } = 4 \vec { i } + \vec { j } + \vec { k }$ Find a vector which is perpendicular to $\vec { v } _ { 1 }$ and $\vec { v } _ { 2 }$ to find an equation of the plane through the point (1, 2, -1)and with normal vector perpendicular to both $\vec { v } _ { 1 }$ and $\vec { v } _ { 2 }$ .Express your answer in the form $A x + B y + C z = D$

Consider the parametric surface $\vec { r } ( s , t ) = s \sin \left( \frac { \pi } { 2 } \right) \vec { i } + s \cos \left( \frac { \pi } { 2 } \right) \vec { j } + 4 t \vec { k }$ Does it contain the y-axis?

Suppose z = f(x, y), f(1, 3)= 5 and $\nabla f ( 1,3 ) = 4 \vec { i } + 5 \vec { j }$ the vector $- 4 \vec { i } + 5 \vec { j } + \vec { k }$ is perpendicular to the graph of f(x, y)at the point (1, 3).

Consider the curve $\vec { r } ( t ) = \left( 2 t ^ { 2 } + 1 \right) \vec { i } + \left( t ^ { 2 } - 2 \right) \vec { j } + t \vec { k }$ Does it pass through the point (1, -2, 0)?

Consider the plane $\vec { r } ( s , t ) = ( - 4 + s - 4 t ) \vec { i } + ( 5 - s + 4 t ) \vec { j } + ( 6 - 4 t - s ) \vec { k }$ Does it contain the point (-7, 8, -7)?

Find a parameterization for the circle of radius 4 in the xz-plane, centered at the point (3, 0, -5).Select all that apply.

Find parametric equations for the cylinder $y ^ { 2 } + z ^ { 2 } = 16$

A vector field $\vec { F } ( x , y )$ is shown below. Find $\vec { F } ( 0,1 )$

A child is sliding down a helical slide.Her position at time t after the start is given in feet by $\vec { r } = \cos t \vec { i } + \sin t \vec { j } + ( 12 - t ) \vec { k }$ .The ground is the xy-plane. At time t = 2 $\pi$ , the child leaves the slide on the tangent to the slide at that point.What is the equation of the tangent line?

Find the parametric equation of the plane through the point (5, 2, 2)and parallel to the lines $\vec { r } ( t ) = ( 1 - 2 t ) \vec { i } + ( 5 + 2 t ) \vec { j } + ( 3 - 4 t ) \vec { k }$ and $\vec { s } ( t ) = ( 3 - 4 t ) \vec { i } + 4 t \vec { j } + ( 4 - 2 t ) \vec { k }$ Select all that apply.

The figure below shows the contour map of a function z = f(x, y). 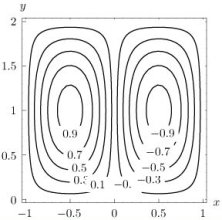Let $\vec{F}$ be the gradient vector field of f, i.e., $\vec{F}=\text { gradf }$ Which of the vector fields show $\vec { F } ?$

Consider the curve $\vec { r } ( t ) = \left( 2 t ^ { 2 } + 1 \right) \vec { i } + \left( t ^ { 2 } + 1 \right) \vec { j } + t \vec { k }$ Does the curve lie on the parametric surface $x = s ^ { 2 } + t ^ { 2 } , y = s ^ { 2 } , z = t ?$

Give parameterizations for a circle of radius 3 in 3-space perpendicular to the y-axis centered at (4, -2, 0).