Deck 7: Integration
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/179
Play
Full screen (f)
Deck 7: Integration
1
Integrate .
A)
B)
C)
D)
A)
B)
C)
D)
2
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)
3
Find the area between and g(x)= x for x 0.Round to 3 decimal places.
0.807
4
Compute .
A)
B)
C)
D)0
A)
B)
C)
D)0

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
5
Use the Fundamental Theorem to evaluate the definite integral 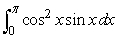 .Reduce fractions and leave them in the form "A/B".
.Reduce fractions and leave them in the form "A/B".
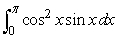 .Reduce fractions and leave them in the form "A/B".
.Reduce fractions and leave them in the form "A/B".
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
6
Find
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
7
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
8
Find an antiderivative of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
10
Find .Hint: Integrate by parts.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
11
Evaluate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose , where a is a constant.Calculate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
14
Calculate the area between the curve 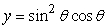 and the x-axis between
and the x-axis between 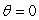 and
and 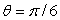 .Round your answer to 2 decimal places.
.Round your answer to 2 decimal places.
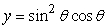 and the x-axis between
and the x-axis between 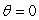 and
and 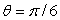 .Round your answer to 2 decimal places.
.Round your answer to 2 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
15
Fuel pressure in the fuel tanks of the space shuttle is decreasing at a rate of 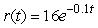 psi per second at time t in seconds.At what rate, in psi/sec, is pressure decreasing at 10 seconds? Round to 2 decimal places.
psi per second at time t in seconds.At what rate, in psi/sec, is pressure decreasing at 10 seconds? Round to 2 decimal places.
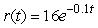 psi per second at time t in seconds.At what rate, in psi/sec, is pressure decreasing at 10 seconds? Round to 2 decimal places.
psi per second at time t in seconds.At what rate, in psi/sec, is pressure decreasing at 10 seconds? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
16
Find
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
17
Compute .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
18
Integrate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose , where a is a constant.Calculate .
A)a
B)7a
C)
D)
A)a
B)7a
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
20
Fuel pressure in the fuel tanks of the space shuttle is decreasing at a rate of 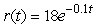 psi per second at time t in seconds.By how many total psi has the pressure decreased during the first minute? Round to 2 decimal places.
psi per second at time t in seconds.By how many total psi has the pressure decreased during the first minute? Round to 2 decimal places.
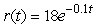 psi per second at time t in seconds.By how many total psi has the pressure decreased during the first minute? Round to 2 decimal places.
psi per second at time t in seconds.By how many total psi has the pressure decreased during the first minute? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
21
Integrate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
22
Calculate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
23
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
24
Use the table of antiderivatives to determine if the following statement is true.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
25
Calculate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
26
, where a is a constant.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
27
For , find a function such that and .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
28
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
29
Calculate
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
30
For , find a function such that and .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
31
Calculate , where a and b are constants.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
32
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
33
Integrate 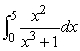 .Give an exact answer and one rounded to 3 decimal places.
.Give an exact answer and one rounded to 3 decimal places.
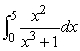 .Give an exact answer and one rounded to 3 decimal places.
.Give an exact answer and one rounded to 3 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
34
Integrate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
35
Calculate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
36
For , find a function such that and .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
37
Use the table of antiderivatives to determine if the following statement is true.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
38
Integrate .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
39
Use the table of antiderivatives to determine if the following statement is true.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
40
, where a is a constant.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
41
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
42
Use the table of antiderivatives to determine if the following statement is true.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
43

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
44
Find the area of the region bounded by y = 0 and 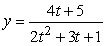 between t = 0 and t = 2.Round to 3 decimal places.
between t = 0 and t = 2.Round to 3 decimal places.
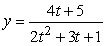 between t = 0 and t = 2.Round to 3 decimal places.
between t = 0 and t = 2.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
45
The following are some of the values for a function known as the Gudermannian function, G(x).
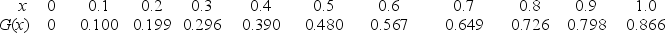 Use these values to approximate the value of
Use these values to approximate the value of 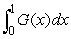 using the trapezoid rule.
using the trapezoid rule.
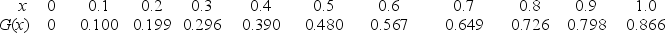 Use these values to approximate the value of
Use these values to approximate the value of 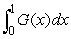 using the trapezoid rule.
using the trapezoid rule.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following gives the area of the circle ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
47
Compute 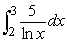 .Round to 3 decimal places.
.Round to 3 decimal places.
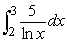 .Round to 3 decimal places.
.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the semicircle of radius 4 pictured below.Which of the following could represent the area of the semicircle? Select all that apply. ![<strong>Consider the semicircle of radius 4 pictured below.Which of the following could represent the area of the semicircle? Select all that apply. </strong> A) \int_{-4}^{4} \sqrt{16-x^{2}} d x B) \frac{1}{2} \cdot \pi \cdot 4^{2} C) 4 \int_{-1}^{1} \sqrt{16+x^{2}} d x D) \left.\frac{1}{2}\left[x \sqrt{16-x^{2}}+16 \arcsin \left(\frac{x}{4}\right)\right]\right|_{-4} ^{4} E) \left.\frac{2}{4}\left[x \sqrt{16-x^{2}}\right]\right|_{-4} ^{4}](https://storage.examlex.com/TB4204/11eb1831_d92d_beb2_88c1_739327c3a9c4_TB4204_00.jpg)
A)
B)
C)
D)
E)
![<strong>Consider the semicircle of radius 4 pictured below.Which of the following could represent the area of the semicircle? Select all that apply. </strong> A) \int_{-4}^{4} \sqrt{16-x^{2}} d x B) \frac{1}{2} \cdot \pi \cdot 4^{2} C) 4 \int_{-1}^{1} \sqrt{16+x^{2}} d x D) \left.\frac{1}{2}\left[x \sqrt{16-x^{2}}+16 \arcsin \left(\frac{x}{4}\right)\right]\right|_{-4} ^{4} E) \left.\frac{2}{4}\left[x \sqrt{16-x^{2}}\right]\right|_{-4} ^{4}](https://storage.examlex.com/TB4204/11eb1831_d92d_beb2_88c1_739327c3a9c4_TB4204_00.jpg)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
49
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
50
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
51
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
52
The following numbers are the left, right, trapezoidal, and midpoint approximations to 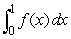 , where f(x)is as shown.(Each uses the same number of subdivisions.)
, where f(x)is as shown.(Each uses the same number of subdivisions.)
• 0.36735
• 0.39896
• 0.36814
• 0.33575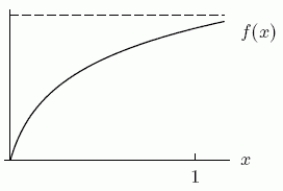 Which one is the midpoint approximation?
Which one is the midpoint approximation?
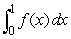 , where f(x)is as shown.(Each uses the same number of subdivisions.)
, where f(x)is as shown.(Each uses the same number of subdivisions.)• 0.36735
• 0.39896
• 0.36814
• 0.33575
 Which one is the midpoint approximation?
Which one is the midpoint approximation?
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
53
Find the area of the region bounded by 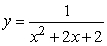 , x = 0, and x = 2.Round to 3 decimal places.
, x = 0, and x = 2.Round to 3 decimal places.
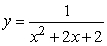 , x = 0, and x = 2.Round to 3 decimal places.
, x = 0, and x = 2.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
54
Compute 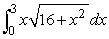 .Round to 3 decimal places.
.Round to 3 decimal places.
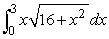 .Round to 3 decimal places.
.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose that as a storm dies down, its rainfall rate (in inches/hour)is given by for 0 t 2, where t is the number of hours since the point of heaviest rainfall.What is the average rainfall rate over these two hours? Round your answer to 3 decimal places.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
56
Find .
A)
B)
C) .
D)
A)
B)
C) .
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
57
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
58
Use the table of antiderivatives to determine if the following statement is true.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
59
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
60
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
61
What is shown in the following graph of ? 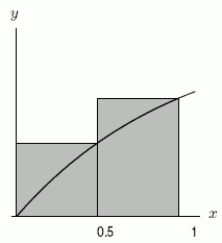
A)The right approximation with n = 2.
B)The midpoint approximation with n = 2.
C)The trapezoid approximation with n = 2.
D)The left approximation with n = 2.

A)The right approximation with n = 2.
B)The midpoint approximation with n = 2.
C)The trapezoid approximation with n = 2.
D)The left approximation with n = 2.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
62
Consider the ellipse pictured below: 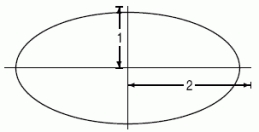 The perimeter of the ellipse is given by the integral .It turns out that there is no elementary antiderivative for the function , and so the integral must be evaluated numerically.A graph of the integrand f( )is shown below.
The perimeter of the ellipse is given by the integral .It turns out that there is no elementary antiderivative for the function , and so the integral must be evaluated numerically.A graph of the integrand f( )is shown below. 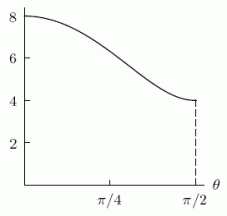 Calculate the right sum that approximates the definite integral with N = 4 equal divisions of the interval.Round to 4 decimal places.
Calculate the right sum that approximates the definite integral with N = 4 equal divisions of the interval.Round to 4 decimal places.
 The perimeter of the ellipse is given by the integral .It turns out that there is no elementary antiderivative for the function , and so the integral must be evaluated numerically.A graph of the integrand f( )is shown below.
The perimeter of the ellipse is given by the integral .It turns out that there is no elementary antiderivative for the function , and so the integral must be evaluated numerically.A graph of the integrand f( )is shown below.  Calculate the right sum that approximates the definite integral with N = 4 equal divisions of the interval.Round to 4 decimal places.
Calculate the right sum that approximates the definite integral with N = 4 equal divisions of the interval.Round to 4 decimal places. 
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
63
The table below shows the velocity v(t)of a falling object at various times (time t measured in seconds, velocity v(t)measured in meters per second). The distance the object fell in these three seconds lies within which interval?
A)(68, 75.5)
B)(75.5, 78)
C)(78, 83)
D)(83, 86.5)
A)(68, 75.5)
B)(75.5, 78)
C)(78, 83)
D)(83, 86.5)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
64
.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
65
Suppose the points are equally spaced and ... .
Is the formula (in terms of f and the 's)for the midpoint Riemann sum approximation to ?
Is the formula (in terms of f and the 's)for the midpoint Riemann sum approximation to ?

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
66
Below is the graph of 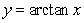 .
. 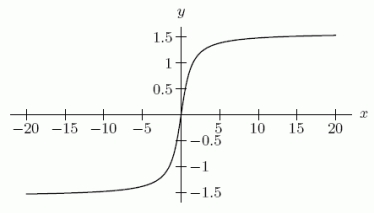 We have the following data:
We have the following data:
For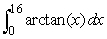 , MID(50)= -12.40537 and TRAP(50)= -12.40041.
, MID(50)= -12.40537 and TRAP(50)= -12.40041.
For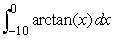 , MID(50)= 21.36379 and TRAP(50)= 21.35097.
, MID(50)= 21.36379 and TRAP(50)= 21.35097.
Using this data alone, what is the best upper bound you can give for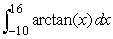 ?
?
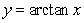 .
.  We have the following data:
We have the following data:For
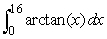 , MID(50)= -12.40537 and TRAP(50)= -12.40041.
, MID(50)= -12.40537 and TRAP(50)= -12.40041.For
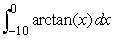 , MID(50)= 21.36379 and TRAP(50)= 21.35097.
, MID(50)= 21.36379 and TRAP(50)= 21.35097.Using this data alone, what is the best upper bound you can give for
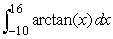 ?
?
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
67
Using two subdivisions, find the left approximation to 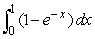 .Round to 4 decimal places.
.Round to 4 decimal places.
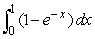 .Round to 4 decimal places.
.Round to 4 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
68
You want to estimate by finding values, A and B, such that < B , with being as small as possible.Which method should you use to find A?
A)The trapezoid rule.
B)The midpoint rule.
C)The left rule.
D)The right rule.
A)The trapezoid rule.
B)The midpoint rule.
C)The left rule.
D)The right rule.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
69
Find the exact value of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the definite integral .Compute the integral using the fundamental theorem of calculus and using the midpoint rule with n = 20.How far apart are your answers?
A)Within 0.03 but not within 0.003
B)Within 0.003 but not within 0.0003
C)Within 0.0003 but not within 0.00003
D)Within 0.00003 but not within 0.000003
A)Within 0.03 but not within 0.003
B)Within 0.003 but not within 0.0003
C)Within 0.0003 but not within 0.00003
D)Within 0.00003 but not within 0.000003

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
71
The midpoint rule gives exact answers for linear functions, no matter how many subdivisions are used.

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
72
For any given function, TRAP(n)is always more accurate than LEFT(n).

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
73
The table below shows the velocity v(t)of a falling object at various times (time t measured in seconds, velocity v(t)measured in meters per second). Due to air resistance, the object's acceleration is decreasing.What does this tell you about the shape of the graph of v(t)?
A)It is concave down
B)It is concave up
C)Neither of the above
A)It is concave down
B)It is concave up
C)Neither of the above

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
74
Consider the definite integral .Compute the integral using the fundamental theorem of calculus and using the trapeziod rule with n = 20.How far apart are your answers?
A)Within 0.1 but not within 0.01
B)Within 0.0001 but not within 0.00001
C)Within 0.001 but not within 0.0001
D)Within 0.01 but not within 0.001
A)Within 0.1 but not within 0.01
B)Within 0.0001 but not within 0.00001
C)Within 0.001 but not within 0.0001
D)Within 0.01 but not within 0.001

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
75
Suppose the points are equally spaced and ... .What is the formula (in terms of f and the 's)for the right Riemann sum approximation to ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the function .Does the midpoint approximation give an exact answer, an overestimate, or an underestimate?
A)An overestimate
B)An underestimate
C)An exact answer
D)Cannot tell
A)An overestimate
B)An underestimate
C)An exact answer
D)Cannot tell

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
77
A drug is being administered intravenously to a patient at a constant rate of 2 mg/hr.The following table shows the rate of change of the amount of the drug in the patient's body at half-hour intervals.Initially there is none of the drug in the patient's body.
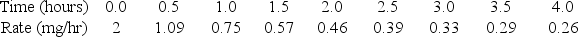 Use the trapezoid rule to estimate of the total amount of the drug in the patient's body after four hours.Round to 2 decimal places.
Use the trapezoid rule to estimate of the total amount of the drug in the patient's body after four hours.Round to 2 decimal places.
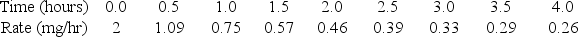 Use the trapezoid rule to estimate of the total amount of the drug in the patient's body after four hours.Round to 2 decimal places.
Use the trapezoid rule to estimate of the total amount of the drug in the patient's body after four hours.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose that a computer takes seconds to add two numbers together, and it takes seconds to multiply two numbers together.The computer is asked to integrate the function from 0 to 1 using left hand sums with n divisions.As a function of n, let T(n)denote the time used by the computer to do the calculation.Compute T(n).(The computer figures x2 as x · x.)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
79
Last Monday we hired a typist to work from 8am to 12 noon.His typing speed decreased between 8am and his 10am cup of coffee, and increased again afterwards, between 10am and noon.His instantaneous speed (measured in characters per second)was measured each hour and the results are given below:
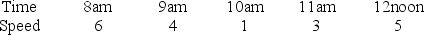 You want to estimate the total number of characters typed between 8am and 12 noon.Find an upper estimate using Reimann sums.
You want to estimate the total number of characters typed between 8am and 12 noon.Find an upper estimate using Reimann sums.
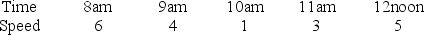 You want to estimate the total number of characters typed between 8am and 12 noon.Find an upper estimate using Reimann sums.
You want to estimate the total number of characters typed between 8am and 12 noon.Find an upper estimate using Reimann sums.
Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate "symbolically" (plug in the limits but don't evaluate).Hint: Integrate by parts using .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 179 flashcards in this deck.
Unlock Deck
k this deck


