Exam 7: Integration

If we approximate $\int_{1}^{\infty} \frac{1}{x^{2}+1} d x$ with $\int_{1}^{b} \frac{1}{x^{2}+1} d x$ what value of b could we use to estimate the value of $\int_{1}^{\infty} \frac{1}{x^{2}+1} d x$ with an error of less than 0.01? Of the following, select the smallest value of b that will work.

Suppose that a computer takes $10^{-7}$ seconds to add two numbers together, and it takes $10^{-5}$ seconds to multiply two numbers together.The computer is asked to integrate the function $f(x)=3 \cdot x^{2}$ from 0 to 1 using left hand sums with n divisions.As a function of n, let T(n)denote the time used by the computer to do the calculation.Compute T(n).(The computer figures x² as x · x.)

Find the area between $f(x)=4 x e^{-x^{2}}$ and g(x)= x for x $\ge$ 0.Round to 3 decimal places.

Use the table of antiderivatives to determine if the following statement is true. $\int \frac{d x}{\sqrt{x^{2}-2 x+2}}=\ln \left|x+\sqrt{x^{2}-2 x+2}\right|+C$

Suppose that as a storm dies down, its rainfall rate (in inches/hour)is given by $y=\frac{1}{0.09+t^{2}}$ for 0 $\le$ t $\le$ 2, where t is the number of hours since the point of heaviest rainfall.What is the average rainfall rate over these two hours? Round your answer to 3 decimal places.

Find the value of A if $\int_{0}^{\sqrt{3}} \frac{x^{2} d x}{1+x^{2}}=\sqrt{3}-\frac{\pi}{A}$ .

Derive the formula for the area of a circle of radius R using trigonometric substitution.

Calculate $\int \sec ^{2} \theta d \theta$

Find $\int(\ln x)^{2} d x$ .Hint: Integrate by parts.

$\int \sin ^{4} x \cos ^{3} x d x=\frac{1}{5} \sin ^{5} x-\frac{1}{7} \sin ^{7} x+C$ .

$\int x^{2}(2 x-2) d x=\frac{x^{4}}{2}-\frac{2 x^{3}}{3}+C$ .

$\int 7 x \ln x d x=\frac{7}{2} x^{2} \ln x+C$ .

Use the Fundamental Theorem to evaluate the definite integral $\int_{0}^{\pi} \cos ^{2} x \sin x d x$ .Reduce fractions and leave them in the form "A/B".

$\int \frac{e^{x}}{1+e^{2 x}} d x=\frac{1}{2} \arctan \left(e^{x}\right)+C$ .

Evaluate exactly: $\int_{x / 2}^{x}(\sin t) e^{\cos t} d t$ .

Evaluate $\int_{0}^{1 / 7} \frac{1}{1-x^{2}} d x$ to 3 decimal places.

Consider the integral $\int_{0}^{\infty} \frac{\sin ^{2} x}{(1+x)^{2}} d x$ .Which if the following is true?

Find $\int\left(\frac{1}{x+1}-\frac{1}{(x+1)^{2}}\right) d x$ .

Consider the ellipse pictured below: 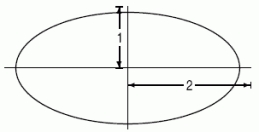The perimeter of the ellipse is given by the integral $\int_{0}^{\pi / 2} 8 \sqrt{1-\frac{3}{4} \sin ^{2} \theta} d \theta$ .It turns out that there is no elementary antiderivative for the function $f(\theta)=8 \sqrt{1-\frac{3}{4} \sin ^{2} \theta}$ , and so the integral must be evaluated numerically.A graph of the integrand f( $\theta$ )is shown below. 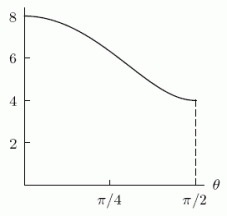Calculate the right sum that approximates the definite integral with N = 4 equal divisions of the interval.Round to 4 decimal places.

$\int(1+x) \sin (4 x) d x=-\frac{\cos 4 x}{4}+\frac{x \cos 4 x}{4}-\frac{\sin 4 x}{16}+C$ .