Deck 10: Approximating Functions Using Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/71
Play
Full screen (f)
Deck 10: Approximating Functions Using Series
1
Use the first three nonzero terms of the Taylor polynomial to approximate .Give your answer to 5 decimal places.
A)0.92868
B)0.92880
C)-0.92880
D)-0.92868
E)does not exist
A)0.92868
B)0.92880
C)-0.92880
D)-0.92868
E)does not exist
0.92880
2
Find the fourth term of the Taylor series for the function about x = 1.
A)
B)
C)
D)
A)
B)
C)
D)
3
Recognize 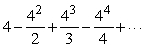 as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
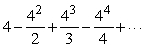 as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.1.6094
4
Approximate the function 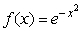 with a Taylor polynomial of degree 6.Use this to estimate the value of
with a Taylor polynomial of degree 6.Use this to estimate the value of 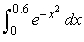 to 5 decimal places.
to 5 decimal places.
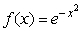 with a Taylor polynomial of degree 6.Use this to estimate the value of
with a Taylor polynomial of degree 6.Use this to estimate the value of 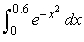 to 5 decimal places.
to 5 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose a function satisfies , , , and .What is the third degree Taylor polynomial for f about x = 5?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
6
The hyperbolic cosine function is defined as follows: .Use the Taylor polynomial for near 0 to find the Taylor polynomial of degree 4 for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
7
Find the fourth term of the Taylor series for the function about .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
8
Find 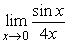 using a Taylor approximation for sin x.
using a Taylor approximation for sin x.
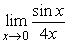 using a Taylor approximation for sin x.
using a Taylor approximation for sin x.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
9
The graph of y = f(x)is given below. 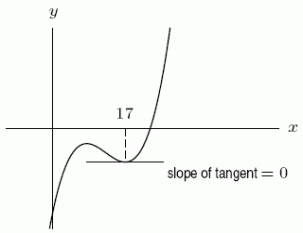 Suppose we approximate f(x)near x = 17 by the second degree Taylor polynomial centered about 17,
Suppose we approximate f(x)near x = 17 by the second degree Taylor polynomial centered about 17, 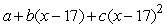 .Is b positive, negative, or zero?
.Is b positive, negative, or zero?
 Suppose we approximate f(x)near x = 17 by the second degree Taylor polynomial centered about 17,
Suppose we approximate f(x)near x = 17 by the second degree Taylor polynomial centered about 17, 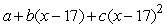 .Is b positive, negative, or zero?
.Is b positive, negative, or zero?
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
10
Find the Taylor polynomial of degree 3 around x = 0 for the function 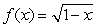 and use it to approximate
and use it to approximate 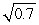 .Give your answer to 4 decimal places.
.Give your answer to 4 decimal places.
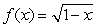 and use it to approximate
and use it to approximate 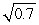 .Give your answer to 4 decimal places.
.Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
11
Approximate the function 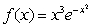 for values of x near 0 using the first three non-zero terms of its Taylor polynomial.
for values of x near 0 using the first three non-zero terms of its Taylor polynomial.
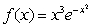 for values of x near 0 using the first three non-zero terms of its Taylor polynomial.
for values of x near 0 using the first three non-zero terms of its Taylor polynomial.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
12
Is the Taylor polynomial of degree 6 for 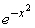 for x near 0 given by
for x near 0 given by 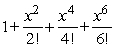 ?
?
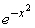 for x near 0 given by
for x near 0 given by 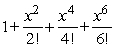 ?
?
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose you approximate and using the Taylor polynomial of degree 3 around x = 0 for the function .Which approximation is more accurate?
A)the approximation of
B)the approximation of
A)the approximation of
B)the approximation of

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
14
What is the fourth degree Taylor polynomial for about x = 0?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
15
Solve 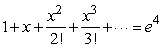 for x.
for x.
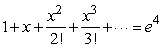 for x.
for x.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
16
Construct the Taylor polynomial approximation of degree 3 to the function 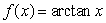 about the point x = 0.Use it to approximate the value
about the point x = 0.Use it to approximate the value 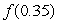 to 5 decimal places.How does the approximation compare to the actual value?
to 5 decimal places.How does the approximation compare to the actual value?
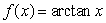 about the point x = 0.Use it to approximate the value
about the point x = 0.Use it to approximate the value 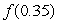 to 5 decimal places.How does the approximation compare to the actual value?
to 5 decimal places.How does the approximation compare to the actual value?
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
17
Recognize 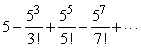 as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
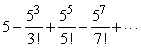 as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
as a Taylor series evaluated at a particular value of x and find the sum to 4 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
18
The function g has the Taylor approximation 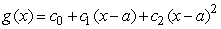 and the graph given below:
and the graph given below: 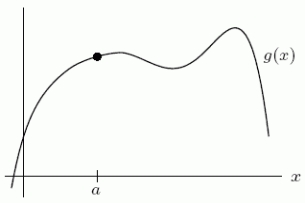 Is c0 positive, negative, or zero?
Is c0 positive, negative, or zero?
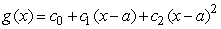 and the graph given below:
and the graph given below:  Is c0 positive, negative, or zero?
Is c0 positive, negative, or zero?
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
19
Estimate 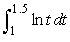 using a 4th degree Taylor Polynomial for
using a 4th degree Taylor Polynomial for 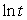 about t = 1.Round to 4 decimal places.
about t = 1.Round to 4 decimal places.
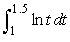 using a 4th degree Taylor Polynomial for
using a 4th degree Taylor Polynomial for 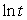 about t = 1.Round to 4 decimal places.
about t = 1.Round to 4 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
20
What is the general term of the series ?
A) for
B) for
C) for
D) for
A) for
B) for
C) for
D) for

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
21
Find the Maclaurin series for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
22
Find an expression for the general term of the Taylor series for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
23
The infinite series does not converge for .What behavior does it exhibit? It does converge for .To what number does it appear to converge?
A)At -1, the series diverges to , At 1, it appears to converge to ln(3).
B)At -1 the series diverges because the terms alternate back and forth between positive and negative.At 1, it appears to converge to ln(2).
C)At -1, the series diverges because some of the terms are undefined.At 1, it appears to converge to ln(3).
D)At -1, the series diverges to .At 1, it appears to converge to ln(2).
A)At -1, the series diverges to , At 1, it appears to converge to ln(3).
B)At -1 the series diverges because the terms alternate back and forth between positive and negative.At 1, it appears to converge to ln(2).
C)At -1, the series diverges because some of the terms are undefined.At 1, it appears to converge to ln(3).
D)At -1, the series diverges to .At 1, it appears to converge to ln(2).

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
24
Find the Taylor series centered at (i.e.the Maclaurin series)for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the function .Is the Maclaurin series for given by ?

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
26
The graph of the function is a bell-shaped curve similar to a normal probability density function.Is the Maclaurin series for ?

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
27
Use the binomial series to find the coefficient of the 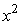 term in the expansion of
term in the expansion of 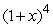 .
.
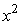 term in the expansion of
term in the expansion of 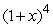 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
28
Based on the Maclaurin series for the function 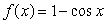 , evaluate
, evaluate 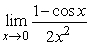 .
.
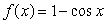 , evaluate
, evaluate 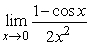 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
29
Find the first four non-zero terms of the Taylor series about zero for the function 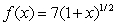 .Leave coefficients in fraction form.
.Leave coefficients in fraction form.
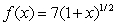 .Leave coefficients in fraction form.
.Leave coefficients in fraction form.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
30
Use the Taylor series for at x = 0 to find the Taylor series for at x = 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
31
According to the theory of relativity, the energy, E, of a body of mass m is given as a function of its speed, v, by 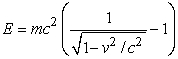 , where c is a constant, the speed of light.Assuming v < c, expand E as a series in v/c, as far as the second non-zero term.If v = 0.05c, approximate E using your expansion.Also, approximate E by the formula
, where c is a constant, the speed of light.Assuming v < c, expand E as a series in v/c, as far as the second non-zero term.If v = 0.05c, approximate E using your expansion.Also, approximate E by the formula 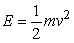 .By what percentage do your two approximations differ?
.By what percentage do your two approximations differ?
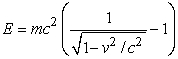 , where c is a constant, the speed of light.Assuming v < c, expand E as a series in v/c, as far as the second non-zero term.If v = 0.05c, approximate E using your expansion.Also, approximate E by the formula
, where c is a constant, the speed of light.Assuming v < c, expand E as a series in v/c, as far as the second non-zero term.If v = 0.05c, approximate E using your expansion.Also, approximate E by the formula 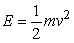 .By what percentage do your two approximations differ?
.By what percentage do your two approximations differ?
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
32
What is the interval of convergence of the Taylor series for the function about zero? (Exclude any possible endpoints.)
A)
B)
C)
D)none of the above
A)
B)
C)
D)none of the above

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
33
Use the formula for the Taylor polynomial approximation to the function 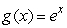 about
about 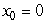 to construct a polynomial approximation of degree 6 for
to construct a polynomial approximation of degree 6 for 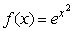 .Use the first four nonzero terms of this approximation to estimate the value of
.Use the first four nonzero terms of this approximation to estimate the value of 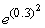 .Give your answer to 5 decimal places.
.Give your answer to 5 decimal places.
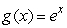 about
about 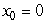 to construct a polynomial approximation of degree 6 for
to construct a polynomial approximation of degree 6 for 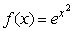 .Use the first four nonzero terms of this approximation to estimate the value of
.Use the first four nonzero terms of this approximation to estimate the value of 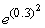 .Give your answer to 5 decimal places.
.Give your answer to 5 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
34
Suppose that you are told that the Taylor series of 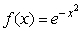 about x = 0 is
about x = 0 is 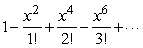 .Find
.Find 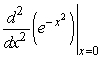 .
.
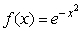 about x = 0 is
about x = 0 is 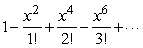 .Find
.Find 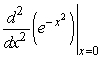 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
35
Find the number to which the series 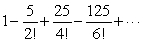 converges.Round to 5 decimal places.
converges.Round to 5 decimal places.
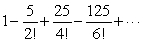 converges.Round to 5 decimal places.
converges.Round to 5 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
36
Solve 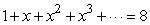 for x.Round to 2 decimal places.
for x.Round to 2 decimal places.
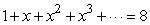 for x.Round to 2 decimal places.
for x.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
37
According to the theory of relativity, the energy, E, of a body of mass m is given as a function of its speed, v, by , where c is a constant, the speed of light.Assuming v < c, expand E as a series in v/c, as far as the second non-zero term.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
38
Use the derivative of the Taylor series about 0 for to find the Taylor series about 0 for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
39
The function is part of the normal probability density function (or bell-shaped curve).Find the Maclaurin series for by first finding the Maclaurin series for and then integrating it term by term.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
40
Use the derivative of the Taylor series about 0 for 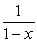 to find the Taylor series about 0 for
to find the Taylor series about 0 for 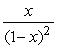 .Use this result to find the value of
.Use this result to find the value of 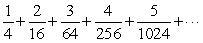 .Round to 3 decimal places.
.Round to 3 decimal places.
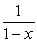 to find the Taylor series about 0 for
to find the Taylor series about 0 for 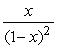 .Use this result to find the value of
.Use this result to find the value of 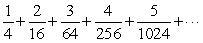 .Round to 3 decimal places.
.Round to 3 decimal places.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
41
Find the first harmonic of the function .
A)
B)
C)
D)
E)0
A)
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
42
Find the second harmonic of the function .
A)
B)
C)
D)
E)0
A)
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
43
Given the fact that the Taylor series about x = 0 for , is the Taylor series about x = 0 for ?

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
44
Find the first harmonic of the function
.
A)
B)
C)
D)
E)0
.
A)
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
45
Find the 12th-degree Taylor polynomial for centered at x = 0.Suppose you use the first two non-zero terms of the polynomial to approximate for 0 < x < 1.Is your approximation too big or too small?
A)Too small
B)Too big
A)Too small
B)Too big

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
46
Estimate using the first two terms of the Taylor series about x = -2 for .
A)
B)
C)
D)20.085537
A)
B)
C)
D)20.085537

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
47
Since 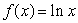 and
and 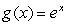 are inverse functions, we know that
are inverse functions, we know that 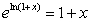 for x > -1.Find the Taylor series for
for x > -1.Find the Taylor series for 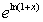 using only up to the quadratic terms and show that the result is 1 + x.
using only up to the quadratic terms and show that the result is 1 + x.
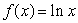 and
and 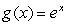 are inverse functions, we know that
are inverse functions, we know that 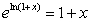 for x > -1.Find the Taylor series for
for x > -1.Find the Taylor series for 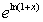 using only up to the quadratic terms and show that the result is 1 + x.
using only up to the quadratic terms and show that the result is 1 + x.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
48
Find the first four terms of the Taylor series about x = -2 for 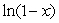 .
.
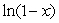 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
49
Use the Maclaurin series for to find the Maclaurin series for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
50
Estimate the magnitude of the error in approximating using a third degree Taylor polynomial about x = 0.
A)0.0125
B)0.0333
C)0.0417
D)0.0625
A)0.0125
B)0.0333
C)0.0417
D)0.0625

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
51
Approximate using the first three terms of the Taylor series about zero for .
A)0.321
B)0.336
C)0.3
D)1.5
A)0.321
B)0.336
C)0.3
D)1.5

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
52
Is a good bound for the maximum possible error for the nth degree Taylor polynomial about x = 0 approximating on the interval [0, 1]?

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
53
Find for the function
.
A)1
B)-1
C)1/2
D)-1/2
E)0
.
A)1
B)-1
C)1/2
D)-1/2
E)0

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
54
Show that the Taylor series about 0 for 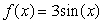 converges to
converges to 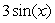 for all values of x by showing that the error
for all values of x by showing that the error 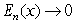 .
.
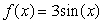 converges to
converges to 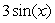 for all values of x by showing that the error
for all values of x by showing that the error 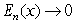 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
55
Find the second harmonic of the function .
A)
B)
C)
D)
E)0
A)
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
56
Find for the function .
A)
B)
C)
D)
E)0
A)
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
57
Find the 12th-degree Taylor polynomial for centered at x = 0.Suppose you use the first two non-zero terms of the series to approximate for 0 < x < 1.Is the magnitude of the error always less than 0.011?

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
58
a) 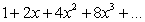 is the Maclaurin series for what function?
is the Maclaurin series for what function?
b)What is its radius and interval of convergence (excluding possible endpoints)?
c)Use the Maclaurin series to determine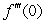 .
.
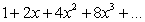 is the Maclaurin series for what function?
is the Maclaurin series for what function?b)What is its radius and interval of convergence (excluding possible endpoints)?
c)Use the Maclaurin series to determine
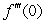 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
59
The function h(x)is a continuous differentiable function whose graph is drawn below.The accompanying table provides some information about h(x)and its derivatives. 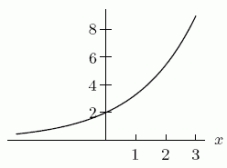 h(x), h'(x), h"(x)and h"'(x)are all increasing functions.Suppose we use a tangent line approximation at zero to approximate h(0.1).Find a good upper bound for the error.
h(x), h'(x), h"(x)and h"'(x)are all increasing functions.Suppose we use a tangent line approximation at zero to approximate h(0.1).Find a good upper bound for the error.
A)0.0025
B)0.0820
C)0.1066
D)0.1558
 h(x), h'(x), h"(x)and h"'(x)are all increasing functions.Suppose we use a tangent line approximation at zero to approximate h(0.1).Find a good upper bound for the error.
h(x), h'(x), h"(x)and h"'(x)are all increasing functions.Suppose we use a tangent line approximation at zero to approximate h(0.1).Find a good upper bound for the error.A)0.0025
B)0.0820
C)0.1066
D)0.1558

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
60
It can be shown that the Maclaurin series for 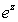 ,
, 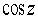 and
and 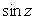 converge for all values of z in the complex numbers, just as they do for all values of x in the real numbers.
converge for all values of z in the complex numbers, just as they do for all values of x in the real numbers.
a)Write down and simplify the Maclaurin series for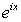 .
.
b)Write down the Maclaurin series for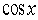 and
and 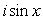 c)Use the series you found in parts a)and b)to show that
c)Use the series you found in parts a)and b)to show that 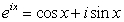 .(This is one of several formulas called "Euler's Formula.")
.(This is one of several formulas called "Euler's Formula.")
d)Find the value of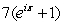 .
.
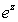 ,
, 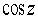 and
and 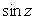 converge for all values of z in the complex numbers, just as they do for all values of x in the real numbers.
converge for all values of z in the complex numbers, just as they do for all values of x in the real numbers.a)Write down and simplify the Maclaurin series for
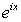 .
.b)Write down the Maclaurin series for
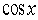 and
and 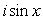 c)Use the series you found in parts a)and b)to show that
c)Use the series you found in parts a)and b)to show that 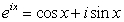 .(This is one of several formulas called "Euler's Formula.")
.(This is one of several formulas called "Euler's Formula.")d)Find the value of
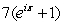 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose that g is the pulse train of width 0.5.What percent of the energy of g is contained in the constant term of its Fourier series? Round to one decimal place.

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
62
a)Find the Taylor series for 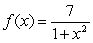 using a series for
using a series for 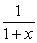 .
.
b)Use the series from part a)to find the Taylor series for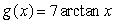 .
.
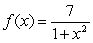 using a series for
using a series for 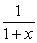 .
.b)Use the series from part a)to find the Taylor series for
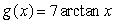 .
.
Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
63
A Taylor polynomial of degree six always has six non-zero terms.

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
64
Medicine balls are launched from the floor to a height of six feet.They bounce, reaching x/10 the height of the previous bounce each time.The heavier the medicine ball, the smaller the value of x.Write a power series that gives the total distance that a medicine ball bounces as a function of x.What is the function that gives this Taylor polynomial?

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
65
Find the second degree Taylor polynomial approximation of about x = 1.
A)
B)
C)
D) .
A)
B)
C)
D) .

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
66
Find the Taylor series for .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
67
Which gives the better approximation of , the Taylor polynomial about zero with three terms, or the Fourier polynomial with three terms?
A)Taylor
B)Fourier
C)Both give the same approximation.
A)Taylor
B)Fourier
C)Both give the same approximation.

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
68
Find the third-degree Fourier polynomial for , where c is a constant, by writing a new function, , with period .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
69
Fill in the blanks: Fourier polynomials give good __________ approximations to a function.Taylor polynomials give good _____________ approximations to a function.

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
70
Use a Taylor polynomial of degree 3 for to approximate the value of .Give your answer to five decimal places.
A)23.66667
B)1.22133
C)2.22554
D)2.20533
A)23.66667
B)1.22133
C)2.22554
D)2.20533

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
71
Use the Taylor polynomials for the sine and cosine functions to find a rational function with a degree 5 numerator and no fractional coefficients that approximates the tangent function near 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck


