Deck 4: Using the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/108
Play
Full screen (f)
Deck 4: Using the Derivative
1
Consider a continuous function with the following properties: 
 for
for  . Which of the following are inconsistent with these four conditions?
. Which of the following are inconsistent with these four conditions?
A)
B) 5
C)
 for
for  . Which of the following are inconsistent with these four conditions?
. Which of the following are inconsistent with these four conditions?A)
B) 5
C)
5
2
Below is the graph of the derivative of a function f, i.e., it is a graph of y = f '(x).Suppose that you are told that = 5.Estimate f(2). 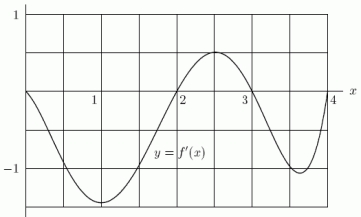
A)3
B)3.5
C)5
D)6.5

A)3
B)3.5
C)5
D)6.5
3.5
3
Starting at time t = 0, water is poured at a constant rate into an empty vase (pictured below).It takes ten seconds for the vase to be filled completely to the top.Let h = f(t)be the depth of the water in the vase at time t.For what value of h is 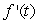 the largest?
the largest?
 the largest?
the largest? 
6
4
Below is the graph of the derivative of a function f, i.e., it is a graph of y = f '(x).Where in the interval 0 x 4 does f achieve its global maximum? 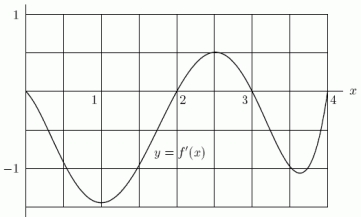
A)0
B)1
C)2
D)3
E)4

A)0
B)1
C)2
D)3
E)4

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
5
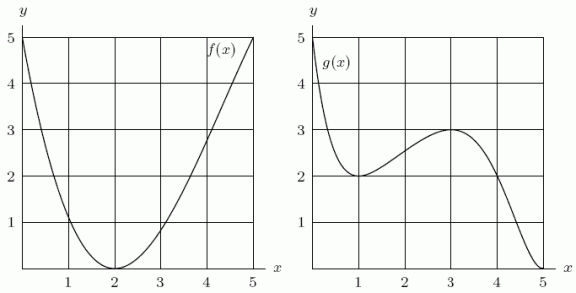
Given below are the graphs of two functions f(x)and g(x).Let 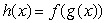 .Is
.Is 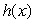 increasing or decreasing on the interval 3 < x < 4?
increasing or decreasing on the interval 3 < x < 4? 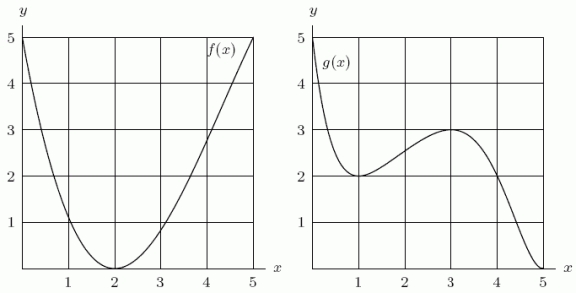
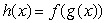 .Is
.Is  increasing or decreasing on the interval 3 < x < 4?
increasing or decreasing on the interval 3 < x < 4? 

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
6
For which interval(s)is the function 16x3 decreasing?
A) -4 or 4
B)-4 4
C)-4 0
D)0 4
E)-4 4,
A) -4 or 4
B)-4 4
C)-4 0
D)0 4
E)-4 4,

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
7
Consider a continuous function with the following properties: 
 for
for  . Which of the following is true?
. Which of the following is true?
A)The graph must have a local maximum for .
B)The graph must not have a local maximum for .
C)The graph may or may not have a local maximum for .
 for
for  . Which of the following is true?
. Which of the following is true?A)The graph must have a local maximum for .
B)The graph must not have a local maximum for .
C)The graph may or may not have a local maximum for .

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
8
Below is the graph of the derivative of a function f, i.e., it is a graph of y = f '(x).Which of the following values of x are local minima of f? 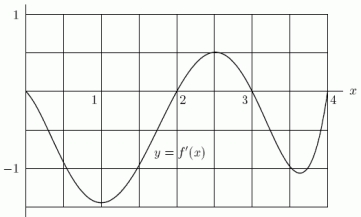
A)2
B)0
C)4
D)3
E)1

A)2
B)0
C)4
D)3
E)1

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
9
Below is the graph of the derivative of a function f, i.e., it is a graph of y = f '(x).Is f increasing or decreasing on the interval ? 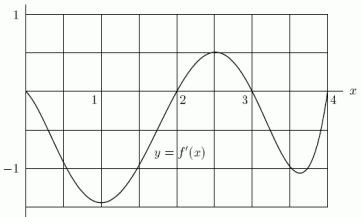


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
10
A water tank is constructed in the shape of a sphere seated atop a circular cylinder.If water is being pumped into the tank at a constant rate, let be the height of the water as a function of time.Which of the following is true at the point where b? 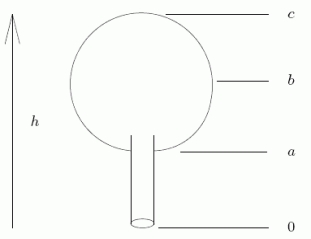
A)The second derivative doesn't exist
B)There is an inflection point
C)The slope is infinite
D)None of the above

A)The second derivative doesn't exist
B)There is an inflection point
C)The slope is infinite
D)None of the above

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
11
Sketch a graph of a function whose 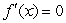 at x=-1,
at x=-1, 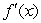 < 0 when x< -1,
< 0 when x< -1, 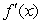 < 0 when x> -1,
< 0 when x> -1,
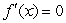 at x=-1,
at x=-1, 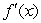 < 0 when x< -1,
< 0 when x< -1, 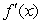 < 0 when x> -1,
< 0 when x> -1,
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
12
Sketch a graph of a function whose 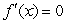 at x=1,
at x=1, 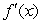 < 0 when x< 1,
< 0 when x< 1, 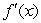 < 0 when x> 1, Is it possible to have
< 0 when x> 1, Is it possible to have 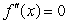 at any value from -2
at any value from -2
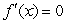 at x=1,
at x=1, 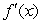 < 0 when x< 1,
< 0 when x< 1, 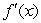 < 0 when x> 1, Is it possible to have
< 0 when x> 1, Is it possible to have 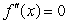 at any value from -2
at any value from -2
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
13
A particle is travelling along the x-axis according to the function 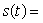 ( t-3 )( t-1 )2.When is the velocity of the particle equal to 0?
( t-3 )( t-1 )2.When is the velocity of the particle equal to 0?
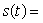 ( t-3 )( t-1 )2.When is the velocity of the particle equal to 0?
( t-3 )( t-1 )2.When is the velocity of the particle equal to 0?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
14
A particle is travelling along the x-axis according to the function 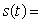 ( t-3 )( t-2 )2.Assuming t
( t-3 )( t-2 )2.Assuming t 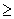 0, when is the acceleration of the particle equal to 0?
0, when is the acceleration of the particle equal to 0?
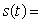 ( t-3 )( t-2 )2.Assuming t
( t-3 )( t-2 )2.Assuming t 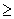 0, when is the acceleration of the particle equal to 0?
0, when is the acceleration of the particle equal to 0?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
15
A water tank is constructed in the shape of a sphere seated atop a circular cylinder.If water is being pumped into the tank at a constant rate, let be the height of the water as a function of time.For the interval a < t < b, which of the following is true? 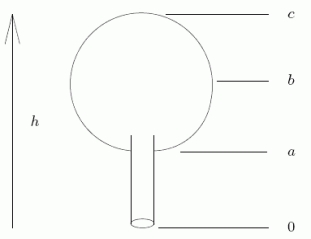
A) is concave down
B) is linear
C) is concave up

A) is concave down
B) is linear
C) is concave up

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
16
Starting at time t = 0, water is poured at a constant rate into an empty vase (pictured below).It takes ten seconds for the vase to be filled completely to the top.Let h = f(t)be the depth of the water in the vase at time t.Is h = f(t)concave up or down on the region 3 < t < 9? 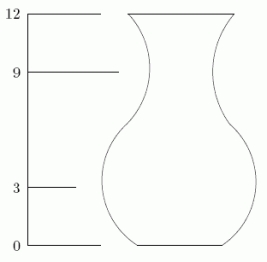


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
17
Given below are the graphs of two functions f(x)and g(x).Let 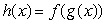 .Is the point x = 1 a local minimum, a local maximum, or neither for the function
.Is the point x = 1 a local minimum, a local maximum, or neither for the function 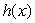 ?
? 
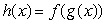 .Is the point x = 1 a local minimum, a local maximum, or neither for the function
.Is the point x = 1 a local minimum, a local maximum, or neither for the function 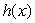 ?
? 

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
18
Given below are the graphs of two functions f(x)and g(x).Graph 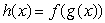 on a similar set of axes.
on a similar set of axes. 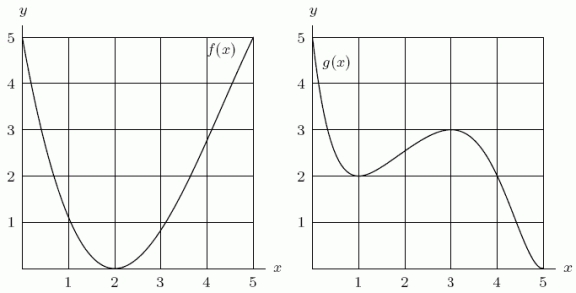
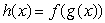 on a similar set of axes.
on a similar set of axes. 

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
19
Below is the graph of the derivative of a function f, i.e., it is a graph of y = f '(x).Suppose that you are told that = 3.Which of the following is an exact expression for ? 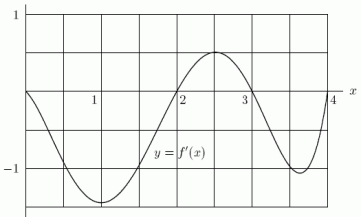
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
20
Determine the equation of the tangent line at x=0 and the value of f(x)at x=1.5 given for all values of a
A)y=(ln a)x+1, y=1.5(ln a)+1
B)y=(ln a)(a1.5)x-1, y=-1
C)y=(a1.5)[(ln a)x-1], y=-1
D)y=(ln a)x-1, y=1.5(ln a)-1
E)y=(ln a)x-1, y=1.5
A)y=(ln a)x+1, y=1.5(ln a)+1
B)y=(ln a)(a1.5)x-1, y=-1
C)y=(a1.5)[(ln a)x-1], y=-1
D)y=(ln a)x-1, y=1.5(ln a)-1
E)y=(ln a)x-1, y=1.5

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the function 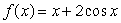 , for
, for 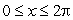 .Is f increasing or decreasing at x = 3.82?
.Is f increasing or decreasing at x = 3.82?
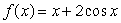 , for
, for 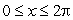 .Is f increasing or decreasing at x = 3.82?
.Is f increasing or decreasing at x = 3.82?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
22
Let f be a function.Is it true or false that the inflection points of f are the local extrema of f '.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
23
Given the table of data about the second derivative of a function f, which of the following types of a function could f be? Assume b > 0.The other constants can be positive or negative.
A)
B)
C)a quadratic (i.e. )
D)a cubic (i.e. )
E)
A)
B)
C)a quadratic (i.e. )
D)a cubic (i.e. )
E)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the function 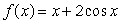 , for
, for 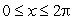 .What is the largest value of f? Round to 2 decimal places.
.What is the largest value of f? Round to 2 decimal places.
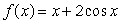 , for
, for 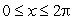 .What is the largest value of f? Round to 2 decimal places.
.What is the largest value of f? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the function 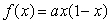 for
for 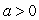 .What is largest value of a such that
.What is largest value of a such that 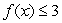 on the region
on the region 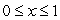 ?
?
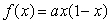 for
for 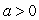 .What is largest value of a such that
.What is largest value of a such that 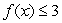 on the region
on the region 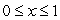 ?
?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the function , for .Which of the following values are inflection points of f?
A)0
B)
C)
D)
E)
A)0
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
27
Consider for .For which value(s)of x is least?
A)0.586
B)-1
C)0
D)3
A)0.586
B)-1
C)0
D)3

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
28
Let , where b is a positive constant.Which of the following are inflection points of f?
A)b
B)
C)
D)
E)0
A)b
B)
C)
D)
E)0

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
29
Consider 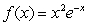 for
for 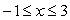 .Is f increasing or decreasing on the interval 0 < x < 2?
.Is f increasing or decreasing on the interval 0 < x < 2?
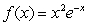 for
for 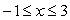 .Is f increasing or decreasing on the interval 0 < x < 2?
.Is f increasing or decreasing on the interval 0 < x < 2?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
30
Let f(x)be a function with positive values and let .If f has a local maximum at , what about g?
A)g has a local maximum at
B)g has a local minimum at
C)g could have a local maximum or a local minimum at
A)g has a local maximum at
B)g has a local minimum at
C)g could have a local maximum or a local minimum at

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the function , for .As a increases, what happens to the horizontal asmyptotes of f?
A)They shift upward.
B)They remain the same.
C)They shift downward.
A)They shift upward.
B)They remain the same.
C)They shift downward.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
32
Below is the graph of the rate r at which people arrive for lunch at Cafeteria Charlotte.Checkers start at 12:00 noon and can pass people through at a constant rate of 5 people/minute.Let f(t)be the length of the line (i.e.the number of people)at time t.Suppose that at 11:50 there are already 150 people lined up.Using the graph together with this information, sketch a graph of f. 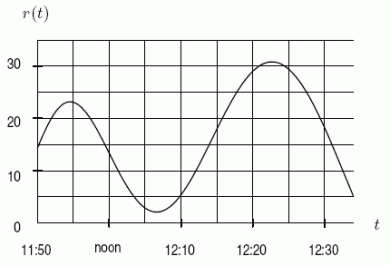


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
33
Below is the graph of the rate r at which people arrive for lunch at Cafeteria Charlotte.Checkers start at 12:00 noon and can pass people through at a constant rate of 5 people/minute.Let f(t)be the length of the line (i.e.the number of people)at time t.Suppose that at 11:50 there are already 150 people lined up.Using the graph together with this information, is the time 12:34 a local minimum, a local maximum, or neither of f? 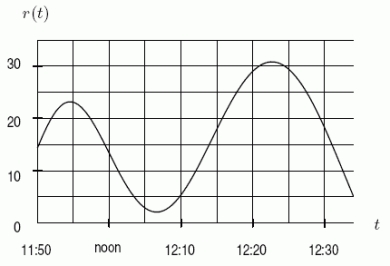


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the function 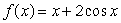 , for
, for 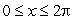 .Graph the function and use your graph to find how many roots there are to the equation
.Graph the function and use your graph to find how many roots there are to the equation 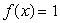 .
.
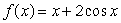 , for
, for 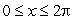 .Graph the function and use your graph to find how many roots there are to the equation
.Graph the function and use your graph to find how many roots there are to the equation 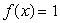 .
.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
35
Below is the graph of the rate r at which people arrive for lunch at Cafeteria Charlotte.Checkers start at 12:00 noon and can pass people through at a constant rate of 5 people/minute.Let f(t)be the length of the line (i.e.the number of people)at time t.Suppose that at 11:50 there are already 150 people lined up.Using the graph together with this information, is f concave up or down on the interval 11:55 < t < 12:07? 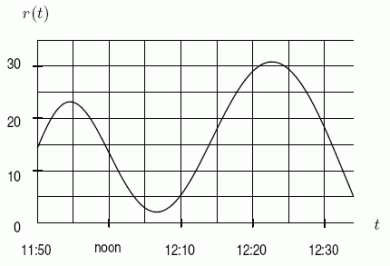


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the two-parameter family of curves , with and .Is the graph concave up or down at the point x = -2?
A)Concave down
B)Concave up
C)It depends on the values of a and b
A)Concave down
B)Concave up
C)It depends on the values of a and b

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the function , for .Where is f increasing most rapidly?
A)0
B)
C)
D)
E)
A)0
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
38
Below is the graph of the rate r at which people arrive for lunch at Cafeteria Charlotte.Checkers start at 12:00 noon and can pass people through at a constant rate of 5 people/minute.Let f(t)be the length of the line (i.e.the number of people)at time t.Suppose that at 11:50 there are already 150 people lined up.Using the graph together with this information, when is the line the longest? 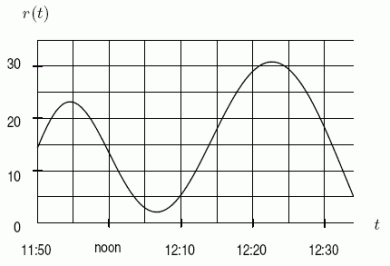


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the function  for
for  .For what value of x on the region
.For what value of x on the region 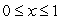 does f have a local maximum? If there is more than one value, give the smallest one.
does f have a local maximum? If there is more than one value, give the smallest one.
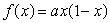 for
for 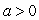 .For what value of x on the region
.For what value of x on the region 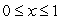 does f have a local maximum? If there is more than one value, give the smallest one.
does f have a local maximum? If there is more than one value, give the smallest one.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
40
Graph the function 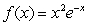 for
for 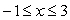 .
.
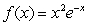 for
for 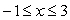 .
.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
41
What does the Extreme Value Theorem allow us to conclude about f if f is continuous on [-10, 80]? Mark all that apply.
A)f has a global maximum on [-10, 80].
B)f has a global minimum on [-10, 80].
C)f has an inflection point on [-10, 80].
D)None of the above
A)f has a global maximum on [-10, 80].
B)f has a global minimum on [-10, 80].
C)f has an inflection point on [-10, 80].
D)None of the above

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
42
The revenue for selling q items is and the total cost is C(q)= 110 + 60q.Which function gives the total profit earned?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
43
A single cell of a bee's honey comb has the shape shown.The surface area of this cell is given by where h, s, are as shown in the picture.Keeping h and s fixed, for what angle, , is the surface area minimal? Round to the nearest one tenth of a degree. 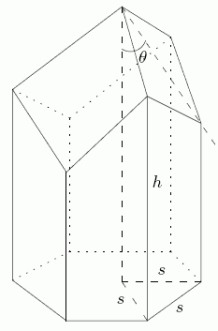


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
44
Write a formula for total cost as a function of quantity r when fixed costs are $30,000 and variable costs are $1,600 per item.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
45
When light strikes a shiny surface, much of it is reflected in the direction shown.However some of it may be scattered on either side of the reflected light.If the intensity (brightness)of the scattered light at the angle (shown in the picture)is I, the Phong model says that where k and n are positive constants depending on the surface.Thus this function gives an idea of how "spread-out" the scattered light is.What effect does decreasing the parameter n have of the graph of I? 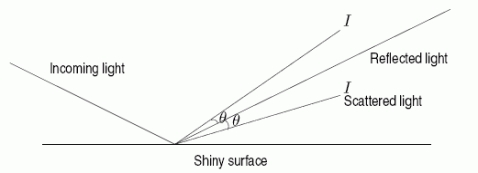
A)The graph drops less quickly
B)The graph stretches upward
C)The graph shrinks downward
D)The graph drops more quickly

A)The graph drops less quickly
B)The graph stretches upward
C)The graph shrinks downward
D)The graph drops more quickly

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
46
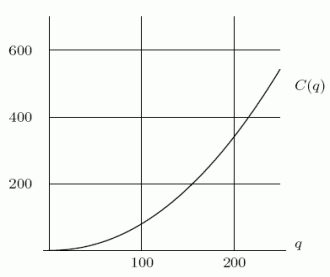
The cost C(q)(in dollars)of producing a quantity q of a certain product is shown in the graph below.Suppose that the manufacturer can sell the product for $2.50 each (regardless of how many are sold), so that the total revenue from selling a quantity q is R(q)= 2.5q.The difference 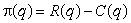 is the total profit.Let
is the total profit.Let 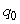 be the quantity that will produce the maximum profit.What is
be the quantity that will produce the maximum profit.What is 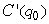 ?
? 
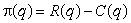 is the total profit.Let
is the total profit.Let 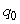 be the quantity that will produce the maximum profit.What is
be the quantity that will produce the maximum profit.What is 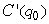 ?
? 

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
47
The cost C(q)(in dollars)of producing a quantity q of a certain product is shown in the graph below.The average cost is given by .Graphically, a(q)is the slope of the line between which two points? 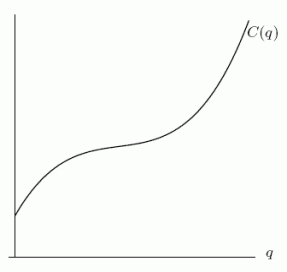
A)(0, 0)
B)
C)(0, q)
D)

A)(0, 0)
B)
C)(0, q)
D)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose f is a cubic function with critical points at x = 8 and x = 6.What is the x-coordinate of the inflection point of f?

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
49
A rectangle is inscribed between the function y= -x2 + 49 and the x-axis.What is the maximum area of the square if the base if two vertices of the square lie on the x-axis?
A)3.5
B)257.25
C)428.75
D)8.042
E)40.459
A)3.5
B)257.25
C)428.75
D)8.042
E)40.459

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
50
Total cost and revenue are approximated by the functions C = 1200 + 3.5q and R = 6q, both in dollars.Identify the marginal cost per item.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the one-parameter family of functions given by for .What are the effects on the graph as the value of A is decreased?
A)The global minimum is decreased.
B)The global minimum is increased.
C)The curvature is decreased (i.e.the curve is wider)
D)The curvature is increased (i.e.the curve is narrower)
A)The global minimum is decreased.
B)The global minimum is increased.
C)The curvature is decreased (i.e.the curve is wider)
D)The curvature is increased (i.e.the curve is narrower)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
52
The revenue for selling q items is 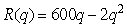 and the total cost is C(q)= 120 + 60q.What quantity maximizes profit?
and the total cost is C(q)= 120 + 60q.What quantity maximizes profit?
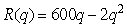 and the total cost is C(q)= 120 + 60q.What quantity maximizes profit?
and the total cost is C(q)= 120 + 60q.What quantity maximizes profit?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
53
If you want to maximize profit, you should minimize average cost.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
54
In the function y=2 sin (x)+1.96, in the interval from 0 , at which value(s)of x does the function contain a global maximum?
A)
B)0
C)
D)4
E)2
A)
B)0
C)
D)4
E)2

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
55
For 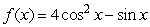 and
and 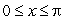 , what is the global maximum value of
, what is the global maximum value of 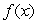 ?
?
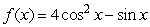 and
and 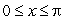 , what is the global maximum value of
, what is the global maximum value of 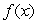 ?
?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
56
The cost C(q)(in dollars)of producing a quantity q of a certain product is shown in the graph below.The average cost is given by .Find on the graph the quantity where a(q)is minimal.Now suppose that the fixed costs (i.e., the costs of setting up before production starts)are doubled.Sketch the new cost function on the same set of axes as the original one and let be the quantity where the new is minimal.Which of the following is true? 
A)
B)
C)
D)Cannot be determined

A)
B)
C)
D)Cannot be determined

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
57
A window with a rectangular base is topped by a semicircle creating a Norman window.A plate of glass 24 ft2 in area.What are the dimensions that would minimize the metal frame around the window? [round to 3 decimal places]
Base: _____________, Height: ________________, Radius: ___________________
Base: _____________, Height: ________________, Radius: ___________________

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
58
Total cost and revenue are approximated by the functions C = 1900 + 4q and R = 6q, both in dollars.Give a formula for the profit function.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
59
In the function y=-4 sin (x)+4.96, in the interval from 0 , what is the global maximum value?
A)0.960
B)8.96
C)4.960
D)0
E)1.571
A)0.960
B)8.96
C)4.960
D)0
E)1.571

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
60
Sketch a graph of a function with two local minima, no global maximum, but a global minimum.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
61
Daily production levels in a plant can be modeled by the function  , which gives units produced t hours after the factory opened at 8am.At what time during the day is factory productivity a maximum? Answer in the form "_:_ _" (without an "am" or "pm").
, which gives units produced t hours after the factory opened at 8am.At what time during the day is factory productivity a maximum? Answer in the form "_:_ _" (without an "am" or "pm").
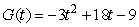 , which gives units produced t hours after the factory opened at 8am.At what time during the day is factory productivity a maximum? Answer in the form "_:_ _" (without an "am" or "pm").
, which gives units produced t hours after the factory opened at 8am.At what time during the day is factory productivity a maximum? Answer in the form "_:_ _" (without an "am" or "pm").
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
62
If you throw a stone into the air at an angle of to the horizontal, it moves along the curve , where y is the height of the stone above the ground, x is the horizontal distance.If the angle is fixed, what value of x gives the maximum height? (Your answer will .)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
63
A student is drinking a milkshake with a straw from a cylindrical cup with a radius of 5.5 cm.If the student is drinking at a rate of 4.5 cm3 per second, then the level of the milkshake dropping at a rate of _____ cm per second.Round to 2 decimal places.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
64
The function 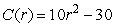 gives cost in dollars of producing r items.What is the marginal cost of increasing r by 1 item from the current production level of r = 6?
gives cost in dollars of producing r items.What is the marginal cost of increasing r by 1 item from the current production level of r = 6?
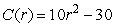 gives cost in dollars of producing r items.What is the marginal cost of increasing r by 1 item from the current production level of r = 6?
gives cost in dollars of producing r items.What is the marginal cost of increasing r by 1 item from the current production level of r = 6?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
65
A rectangular swimming pool is 10 meters long and 6 meters wide.It has a depth of 1 meter at the shallow end, then slopes to a depth of 1.5 meters at the deep end, as shown in the following cross section (not to scale).It is being filled with a hose at a rate of 50,000 cubic centimeters per minute.225 minutes after the hose is turned on, the water is rising at a rate of _____ cm per second.Round to 3 decimal places. 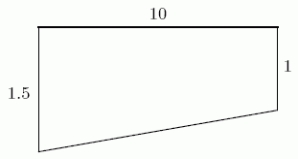


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
66
The function 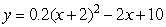 gives the population of a town (in 1000's of people)at time x where x is the number of years since 1980.When was the population a minimum? Round to the nearest year.
gives the population of a town (in 1000's of people)at time x where x is the number of years since 1980.When was the population a minimum? Round to the nearest year.
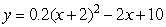 gives the population of a town (in 1000's of people)at time x where x is the number of years since 1980.When was the population a minimum? Round to the nearest year.
gives the population of a town (in 1000's of people)at time x where x is the number of years since 1980.When was the population a minimum? Round to the nearest year.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
67
Find the quantity q which maximizes profit if the total revenue, R(q), and the total cost, C(q), are given in dollars by 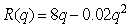
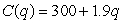 , where
, where 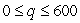 units.
units.
Round to the nearest whole number.
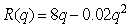
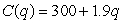 , where
, where 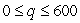 units.
units.Round to the nearest whole number.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
68
If you throw a stone into the air at an angle of to the horizontal, it moves along the curve ,
where y is the height of the stone above the ground, x is the horizontal distance.Suppose the stone is to be thrown over a wall at a fixed horizontal distance l away from you.If you can vary , what is the highest wall that the stone can go over? (Your answer will contain l.)
where y is the height of the stone above the ground, x is the horizontal distance.Suppose the stone is to be thrown over a wall at a fixed horizontal distance l away from you.If you can vary , what is the highest wall that the stone can go over? (Your answer will contain l.)

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
69
What is the shortest distance from the point (0,1)to the curve 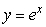 ? You will need to use a calculator with root-finding capabilities.Give your answer to 2 decimal places.
? You will need to use a calculator with root-finding capabilities.Give your answer to 2 decimal places.
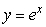 ? You will need to use a calculator with root-finding capabilities.Give your answer to 2 decimal places.
? You will need to use a calculator with root-finding capabilities.Give your answer to 2 decimal places.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
70
A fan is watching a 100-meter footrace from a seat in the bleachers 15 meters back from the midway point.The winning runner is moving approximately 8 meters per second.How fast is the distance from the fan to the winning runner changing when he is x meters into the race?

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
71
A cupful of olive oil falls on the floor forming a circular puddle.Its radius is increasing at a constant rate of 0.2 cm/sec.What is the rate of increase in the area of the olive oil when its circumference measures 20  cm?
cm?
 cm?
cm?
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
72
A bar of ice cream, with dimensions of 3 cm by 3 cm by 3 cm placed on a mesh screen on top of a cylindrical funnel that is 6 cm high and 6 cm in diameter.If the ice cream is melting at a rate of 3.3 into the funnel, what is the rate of change of the height of the funnel when half of the ice cream has melted?
A)0.232
B)0.032
C)0.132
D)0.284
E)0.083
A)0.232
B)0.032
C)0.132
D)0.284
E)0.083

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
73
A submarine can travel 30mi/hr submerged and 60mi/hr on the surface.The submarine must stay submerged if within 200 miles of shore.Suppose that this submarine wants to meet a surface ship 200 miles off shore.The submarine leaves from a port 300 miles along the coast from the surface ship.What route of the type sketched below should the sub take to minimize its time to rendezvous? Give the value of y to 2 decimal places. 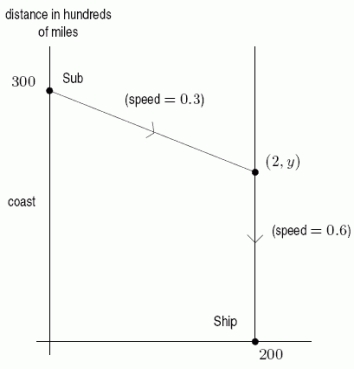


Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
74
A spherical lollipop has a circumference of 7.9 centimeters.A student decides to measure the rate of change of the volume of the lollipop, in ![A spherical lollipop has a circumference of 7.9 centimeters.A student decides to measure the rate of change of the volume of the lollipop, in per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ]](https://storage.examlex.com/TB4204/11eb1831_d960_1965_88c1_eba0f392e0fd_TB4204_11.jpg) per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[
per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ![A spherical lollipop has a circumference of 7.9 centimeters.A student decides to measure the rate of change of the volume of the lollipop, in per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ]](https://storage.examlex.com/TB4204/11eb1831_d960_1966_88c1_67846f56baf0_TB4204_11.jpg) ]
]
![A spherical lollipop has a circumference of 7.9 centimeters.A student decides to measure the rate of change of the volume of the lollipop, in per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ]](https://storage.examlex.com/TB4204/11eb1831_d960_1965_88c1_eba0f392e0fd_TB4204_11.jpg) per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[
per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ![A spherical lollipop has a circumference of 7.9 centimeters.A student decides to measure the rate of change of the volume of the lollipop, in per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ]](https://storage.examlex.com/TB4204/11eb1831_d960_1966_88c1_67846f56baf0_TB4204_11.jpg) ]
]
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
75
A normal distribution in statistics is modeled by the function determine where the maximum value of the function would occur.
A)-2
B)-1
C)0
D)-2
E) -2
A)-2
B)-1
C)0
D)-2
E) -2

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
76
Find the marginal cost for q = 100 when the fixed costs in dollars are 1000, the variable costs are $190 per item, and each sells for $310.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
77
The regular air fare between Boston and San Francisco is $600.An airline flying 747s with a capacity of 480 on this route observes that they fly with an average of 400 passengers.Market research tells the airlines' managers that each $20 fare reduction would attract, on average, 20 more passengers for each flight.How should they set the fare to maximize their revenue?

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
78
The number of plants in a terrarium is given by the function 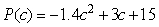 , where c is the number of mg of plant food added to the terrarium.Find the amount of plant food that produces the highest number of plants.Round to 2 decimal places.
, where c is the number of mg of plant food added to the terrarium.Find the amount of plant food that produces the highest number of plants.Round to 2 decimal places.
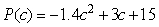 , where c is the number of mg of plant food added to the terrarium.Find the amount of plant food that produces the highest number of plants.Round to 2 decimal places.
, where c is the number of mg of plant food added to the terrarium.Find the amount of plant food that produces the highest number of plants.Round to 2 decimal places.
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
79
Air is being blown into a spherical balloon at a rate of 70 cm3 per second.At what rate is the surface area of the balloon increasing when the radius is 10 cm? Round to 2 decimal places, and do not include units.

Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck
80
A Brian's candy sugar wand is made from flavored sugar inside a straw.The straw is 210 mm long and 5 mm in diameter.The child accidentally poked a hole in the bottom, making the height of the sugar fall at a rate of 1 mm per second.The child realizes that there is a hole after 1 seconds.What was the rate of change of the volume of the sugar at this time?
[![A Brian's candy sugar wand is made from flavored sugar inside a straw.The straw is 210 mm long and 5 mm in diameter.The child accidentally poked a hole in the bottom, making the height of the sugar fall at a rate of 1 mm per second.The child realizes that there is a hole after 1 seconds.What was the rate of change of the volume of the sugar at this time? [ ]](https://storage.examlex.com/TB4204/11eb1831_d95f_f252_88c1_6360e63034c0_TB4204_11.jpg) ]
]
[
![A Brian's candy sugar wand is made from flavored sugar inside a straw.The straw is 210 mm long and 5 mm in diameter.The child accidentally poked a hole in the bottom, making the height of the sugar fall at a rate of 1 mm per second.The child realizes that there is a hole after 1 seconds.What was the rate of change of the volume of the sugar at this time? [ ]](https://storage.examlex.com/TB4204/11eb1831_d95f_f252_88c1_6360e63034c0_TB4204_11.jpg) ]
]
Unlock Deck
Unlock for access to all 108 flashcards in this deck.
Unlock Deck
k this deck


