Exam 4: Using the Derivative
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
The equations describe the motion of a particle moving on a circle.Assume x and y are in miles and t is in days.What is the radius of the circle (in miles)? Round to 2 decimal places.
Free
(Short Answer)
4.7/5  (38)
(38)
Correct Answer:
0.64
Consider the function , for .Which of the following values are inflection points of f?
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
C, E
A particle is travelling along the x-axis according to the function ( t-3 )( t-1 )2.When is the velocity of the particle equal to 0?
Free
(Short Answer)
4.8/5  (34)
(34)
Correct Answer:
t=1, t=5/3=1.667
Sketch a graph of a function with two local minima, no global maximum, but a global minimum.
(Essay)
4.9/5  (34)
(34)
In the function y=-4 sin (x)+4.96, in the interval from 0 , what is the global maximum value?
(Multiple Choice)
5.0/5  (34)
(34)
Write a formula for total cost as a function of quantity r when fixed costs are $30,000 and variable costs are $1,600 per item.
(Short Answer)
5.0/5  (37)
(37)
Consider for .Is f increasing or decreasing on the interval 0 < x < 2?
(Short Answer)
4.9/5  (42)
(42)
Total cost and revenue are approximated by the functions C = 1900 + 4q and R = 6q, both in dollars.Give a formula for the profit function.
(Short Answer)
4.9/5  (34)
(34)
One fine day you take a hike up a mountain path.Using your trusty map you have determined that the path is approximately in the shape of the curve .Here y is the elevation in feet above sea level and x is the horizontal distance in miles you have traveled, but your map only shows the path for 7 miles, horizontal distance.Where on the path is a nice flat place to stop for a picnic?
(Multiple Choice)
4.8/5  (34)
(34)
A Brian's candy sugar wand is made from flavored sugar inside a straw.The straw is 210 mm long and 5 mm in diameter.The child accidentally poked a hole in the bottom, making the height of the sugar fall at a rate of 1 mm per second.The child realizes that there is a hole after 1 seconds.What was the rate of change of the volume of the sugar at this time?
[ ]
(Essay)
4.9/5  (39)
(39)
The function gives cost in dollars of producing r items.What is the marginal cost of increasing r by 1 item from the current production level of r = 6?
(Short Answer)
4.9/5  (28)
(28)
Daily production levels in a plant can be modeled by the function , which gives units produced t hours after the factory opened at 8am.At what time during the day is factory productivity a maximum? Answer in the form "_:_ _" (without an "am" or "pm").
(Short Answer)
4.8/5  (41)
(41)
Consider the function , for .Where is f increasing most rapidly?
(Multiple Choice)
4.7/5  (34)
(34)
Given below are the graphs of two functions f(x)and g(x).Graph on a similar set of axes. 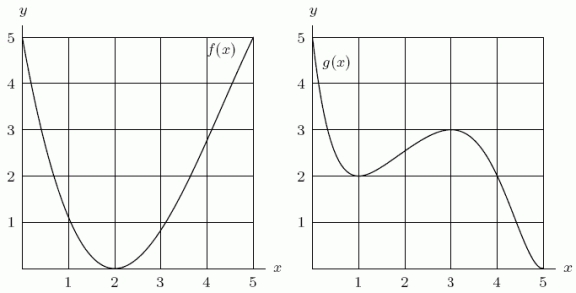
(Essay)
4.8/5  (47)
(47)
Consider the function , for .As a increases, what happens to the horizontal asmyptotes of f?
(Multiple Choice)
4.8/5  (37)
(37)
Showing 1 - 20 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)