Deck 6: Random Variables and Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/72
Play
Full screen (f)
Deck 6: Random Variables and Probability Distributions
1
If x is a random variable, and random variable y is defined as follows, y = a + bx, then 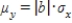 .
.
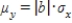 .
.False
2
Which of the following random variables are continuous? I). the air pressure in an automobile tire (in pounds per square inch)II). the diameter of an automobile tire (in centimeters)III). the number of miles traveled by an automobile tire
A)I only
B)I and III only
C)II and III only
D)I, II, and III
E)None of the variables is continuous.
A)I only
B)I and III only
C)II and III only
D)I, II, and III
E)None of the variables is continuous.
None of the variables is continuous.
3
If random variables  and
and  are independent, then
are independent, then 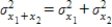 .
.
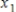 and
and  are independent, then
are independent, then 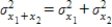 .
.True
4
Determine the area under the z curve to the right of -1.82
A)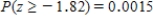
B)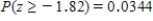
C)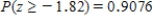
D)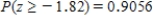
E)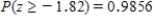
A)
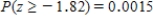
B)
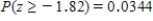
C)
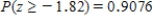
D)
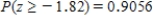
E)
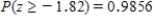

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
5
For a discrete random variable, 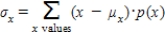 .
.
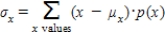 .
.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
6
A random variable is continuous if the set of possible values includes an entire interval on the number line.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
7
A gasoline tank for a certain car is designed to hold 19 gallons of gas. Suppose that the random variable x = actual capacity of a randomly selected tank has a distribution that is well approximated by a normal curve with mean 19.0 gallons and standard deviation 0.2 gallon.
What is the probability that a randomly selected tank will hold at least 18.9 gallons?
A)0.19
B)0.69
C)1
D)0.31
E)0.81
What is the probability that a randomly selected tank will hold at least 18.9 gallons?
A)0.19
B)0.69
C)1
D)0.31
E)0.81

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
8
For random variables, x and y, if y = a + bx, then 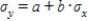 .
.
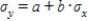 .
.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that fund-raisers at a university call recent graduates to request donations for campus outreach programs. They report the following information for last year's graduates:  Consider the variable x = amount of donation for a person selected at random from the population of last year's graduates of this university.What is
Consider the variable x = amount of donation for a person selected at random from the population of last year's graduates of this university.What is 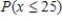 ?
?
A)0.10
B)0.50
C)0.55
D)0.75
E)0.90
 Consider the variable x = amount of donation for a person selected at random from the population of last year's graduates of this university.What is
Consider the variable x = amount of donation for a person selected at random from the population of last year's graduates of this university.What is 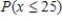 ?
?A)0.10
B)0.50
C)0.55
D)0.75
E)0.90

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
10
For a discrete random variable x, 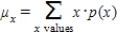 .
.
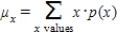 .
.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose x is a continuous random variable with the probability distribution shouwn below. 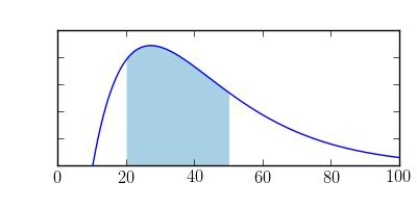 What probability is represented by the shaded area?
What probability is represented by the shaded area?
A)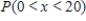
B)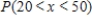
C)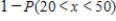
D)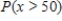
E)none of these
 What probability is represented by the shaded area?
What probability is represented by the shaded area?A)
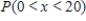
B)
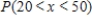
C)
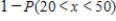
D)
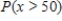
E)none of these

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
12
For a continuous random variable x, the height of the density curve over an interval a to b represents the probability that x is between a and b.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following random variables are discrete? I). the volume of a balloon in liters
II)) the number of helium atoms in a balloon
II)) the number of balloons at a birthday party
A)I only
B)II only
C)III only
D)II and III only
E)I, II, and III
II)) the number of helium atoms in a balloon
II)) the number of balloons at a birthday party
A)I only
B)II only
C)III only
D)II and III only
E)I, II, and III

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
14
A random variable is discrete if the value of the random variable depends upon the outcome of a chance experiment.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
15
For every random variable, 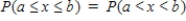 .
.
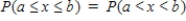 .
.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
16
The standard normal distribution has a mean of 1 and standard deviation of 0.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
17
The distribution of all values of a random variable is called a normal distribution.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
18
A box contains four slips of paper marked 1, 2, 3, and 4. Two slips are selected without replacement. List the possible values for the following random variable. x= number of slips marked "1"
A) 0,1
B) 0,1,2
C)2
D)0
E)1
A) 0,1
B) 0,1,2
C)2
D)0
E)1

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
19
A normal probability plot suggests that a normal probability model is plausible if there is no obvious pattern in the scatter of points.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
20
A chemical supply company currently has in stock 100 pounds of a certain chemical, which it sells to customers in 5-pound lots. Let 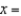 the number of lots ordered by a randomly chosen customer. The probability distribution of x is as follows:
the number of lots ordered by a randomly chosen customer. The probability distribution of x is as follows:  Calculate the mean value of x.
Calculate the mean value of x.
A)2.2
B)2.5
C)2.7
D)3.3
E)3.7
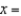 the number of lots ordered by a randomly chosen customer. The probability distribution of x is as follows:
the number of lots ordered by a randomly chosen customer. The probability distribution of x is as follows:  Calculate the mean value of x.
Calculate the mean value of x.A)2.2
B)2.5
C)2.7
D)3.3
E)3.7

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
21
A business has five customer service telephone lines. Let x denote the number of lines in use at any given time. Suppose that the probability distribution of x is as follows:  Find the standard deviation of x. Round your answer to two decimal places.
Find the standard deviation of x. Round your answer to two decimal places.
A)2.5
B)1.33
C)0.98
D)1.22
E)1.25
 Find the standard deviation of x. Round your answer to two decimal places.
Find the standard deviation of x. Round your answer to two decimal places.A)2.5
B)1.33
C)0.98
D)1.22
E)1.25

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
22
From your own experience, give an example of a continuous random variable and a discrete random variable. In a few sentences, explain why each is categorized as continuous or discrete.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
23
What is a random variable?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
24
At the University of Tough Love, good grades in math are very hard to come by. The grade distribution is shown in the table below:  Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
a)ABC
b)CCF
c)BBA
 Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.a)ABC
b)CCF
c)BBA

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
25
Fifty-five percent of the students at Thomas Jefferson High School use "lunch cards" to charge their lunch, rather than bringing money to school. Assuming that the method of payment (cash or lunch card) for one student is independent of the method of payment for the next student in line, what is the probability of observing the following sequence for the first five students through the lunch line?
Cash, Card, Cash, Card, Cash
Cash, Card, Cash, Card, Cash

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
26
During World War II The German forces launched "flying-bombs" (missiles) against London. In a study of the effectiveness of these flying-bombs, a researcher divided the south of London into 575 squares of area equal to 0.25 square km and counted the number of these squares that had sustained exactly k hits. The data for 0 - 4 hits in an area is given in the table below.  Let the random variable x = number of flying-bombs hitting in a randomly selected square in south London.
Let the random variable x = number of flying-bombs hitting in a randomly selected square in south London. 
Probability histogram
b)Using your estimated probabilities in part (a), estimate the following:
i)P(x = 1), the probability that 1 flying bomb hit in a randomly selected square.
ii)P(x < 3), the probability that fewer than 3 flying bombs hit.
iii)P(x ≥ 3), the probability that at least 3 flying bombs hit.
 Let the random variable x = number of flying-bombs hitting in a randomly selected square in south London.
Let the random variable x = number of flying-bombs hitting in a randomly selected square in south London. 
Probability histogram

b)Using your estimated probabilities in part (a), estimate the following:
i)P(x = 1), the probability that 1 flying bomb hit in a randomly selected square.
ii)P(x < 3), the probability that fewer than 3 flying bombs hit.
iii)P(x ≥ 3), the probability that at least 3 flying bombs hit.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
27
In a major study by the statistics classes at Jefferson High School, parking spaces were examined for compliance with the requirement to put money in the meters. Overall, the students found that 80% of metered parking places had meters that had not expired, and 20% had expired. If the traffic officer in charge of ticketing cars with expired meters, and starts at a random location in the City, what is the probability he or she will find an expired meter before the 3rd one?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
28
Thirty-seven percent of the customers of a grocery store use an express checkout. Consider four randomly selected customers, and let x denote the number among the four who use the express checkout.
Calculate .
.
A)0.53
B)0.85
C)0.70
D)0.30
E)0.50
Calculate
 .
.
A)0.53
B)0.85
C)0.70
D)0.30
E)0.50

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
29
The famous physicist, Ernest Rutherford, was a pioneer in the study of radioactivity using electricity. In one experiment he observed the number of particles reaching a counter during time 1700 intervals of 7.5 seconds each. The number of intervals that had 0 - 4 particles reaching the counter is given in the table below.  Let the random variable x = number of particles counted in a 7.5 second time period.
Let the random variable x = number of particles counted in a 7.5 second time period. 
Probability histogram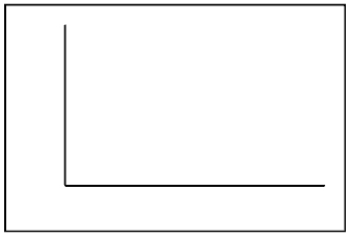
b)Using the estimated probabilities in part (a), estimate the following:
i)P(x = 1), the probability that 1 particle was counted in 7.5 seconds.
ii)P(x < 3), the probability that fewer than 3 particles were counted.
iii)P(x ≥ 3), the probability that at least 3 particles were counted.
 Let the random variable x = number of particles counted in a 7.5 second time period.
Let the random variable x = number of particles counted in a 7.5 second time period. 
Probability histogram

b)Using the estimated probabilities in part (a), estimate the following:
i)P(x = 1), the probability that 1 particle was counted in 7.5 seconds.
ii)P(x < 3), the probability that fewer than 3 particles were counted.
iii)P(x ≥ 3), the probability that at least 3 particles were counted.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
30
Using the notation C = continuous and D = discrete, indicate whether each of the random variables are discrete or continuous.
a)The number of defective lights in your school's main hallway
b)The barometric pressure at midnight
c)The number of staples left in a stapler
d)The number of sentences in a short story
e)The average oven temperature during the cooking of a turkey
f)The number of lightning strikes during a thunderstorm
a)The number of defective lights in your school's main hallway
b)The barometric pressure at midnight
c)The number of staples left in a stapler
d)The number of sentences in a short story
e)The average oven temperature during the cooking of a turkey
f)The number of lightning strikes during a thunderstorm

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
31
One common method used to forecast the results of elections is to take an "exit poll," asking people who they supported as they come out of the voting place. Suppose Smith and Jones are running for City Dogcatcher. In point of fact, 60% of the voting public in the neighborhood of the polling place support Smith. Assuming that the candidate of choice for a voter leaving the polling place is independent of the candidate of choice for the next person to leave, what is the probability that the first 5 voters to leave the polling place would have this sequence for candidate of choice?
Smith, Smith, Smith, Jones, Smith
Smith, Smith, Smith, Jones, Smith

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
32
What information about a probability distribution do the mean and standard deviation of a random variable provide?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
33
In a certain very large city, the Department of Transportation (D.O.T.) has organized a complex system of bus transportation. In an advertising campaign, citizens are encouraged to use the new "GO-D.O.T!" system and head for the nearest bus stop to be transported to and from the central city. Suppose that at one of the bus stops the amount of time (in minutes) that a commuter must wait for a bus is a uniformly distributed random variable, T. The values of T run from 0 minutes to 30 minutes.
a)Sketch the probability distribution of T.
b)What is the probability that a random commuter will spend more than 12 minutes waiting for GO-D.O.T?
a)Sketch the probability distribution of T.
b)What is the probability that a random commuter will spend more than 12 minutes waiting for GO-D.O.T?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
34
In a certain very large city, the Department of Transportation (D.O.T.) has organized a complex system of bus transportation. In an advertising campaign, citizens are encouraged to use the new "GO-D.O.T!" system and head for the nearest bus stop to be transported to and from the central city. Suppose that at one of the bus stops the amount of time (in minutes) that a commuter must wait for a bus is a uniformly distributed random variable, T. The possible values of T run from 0 minutes to 20 minutes.
a)Sketch the probability distribution of T.
b)What is the probability that a randomly selected commuter will spend more than 7 minutes waiting for GO-D.O.T?
a)Sketch the probability distribution of T.
b)What is the probability that a randomly selected commuter will spend more than 7 minutes waiting for GO-D.O.T?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
35
In a major study by the statistics classes at Washington High School, city parking spaces were examined for compliance with the requirement to put money in the parking meters. Overall, the students found that 76% of metered parking places had meters that had not expired, and 24% had meters that were expired. If the traffic officer in charge of ticketing cars with expired meters checks meters at random, what is the probability he or she will find an expired meter before the 3rd one?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
36
The density curve for a continuous random variable is shown below. Use this curve to find the following probabilities:
a)P(x < 1)b)P(2 < x < 3)c)P(x is at least 3)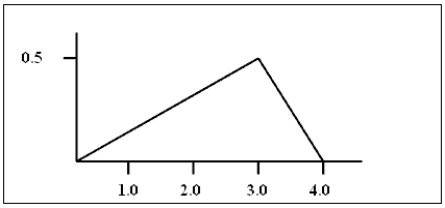 You may use the following area formulas in your calculations:
You may use the following area formulas in your calculations:
Area of a rectangle:
A = lw
Area of a trapezoid: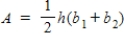 Area of a right triangle:
Area of a right triangle: 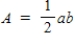
a)P(x < 1)b)P(2 < x < 3)c)P(x is at least 3)
 You may use the following area formulas in your calculations:
You may use the following area formulas in your calculations:Area of a rectangle:
A = lw
Area of a trapezoid:
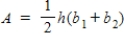 Area of a right triangle:
Area of a right triangle: 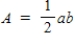

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
37
At the College of Warm & Fuzzy, good grades in math are very easy to come by. The grade distribution is given in the table below:  Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
a)BAC
b)CFF
c)ABA
 Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.a)BAC
b)CFF
c)ABA

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
38
Using the notation C = continuous and D = discrete, indicate whether each of the random variables are discrete or continuous.
a)The number of stair steps to the principal's office
b)The average night time temperature in July at the top of Long's Peak in Colorado
c)The number of forks in your kitchen
d)The number of sentences in a short story
e)The circumference of a California redwood tree
f)The number of grains of sand it takes to fill a quart jar
a)The number of stair steps to the principal's office
b)The average night time temperature in July at the top of Long's Peak in Colorado
c)The number of forks in your kitchen
d)The number of sentences in a short story
e)The circumference of a California redwood tree
f)The number of grains of sand it takes to fill a quart jar

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
39
The density curve for a continuous random variable is shown below. Use this curve to find the following probabilities:
a)P(x < 1)b)P(2 < x < 3)c)P(x is at least 3)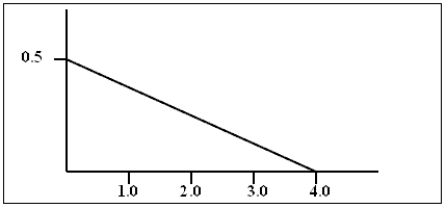 You may use the following area formulas in your calculations:
You may use the following area formulas in your calculations:
Area of a rectangle:
A = lw
Area of a trapezoid: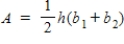 Area of a right triangle:
Area of a right triangle: 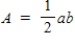
a)P(x < 1)b)P(2 < x < 3)c)P(x is at least 3)
 You may use the following area formulas in your calculations:
You may use the following area formulas in your calculations:Area of a rectangle:
A = lw
Area of a trapezoid:
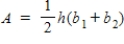 Area of a right triangle:
Area of a right triangle: 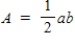

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
40
The sales of a newsmagazine vary from week to week, depending on the importance of the news of the previous week. From empirical data over many years, the following distribution of sales (rounded to the nearest million) has been carefully constructed. What are the mean and standard deviation of this distribution? 


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
41
Inspecting meat is a very important part of the process of ensuring healthy food. So that meat inspectors do not fall into a pattern of inspection, they use a 4-sided die to decide whether or not to sample the meat from a particular "side" of beef. The meat inspector rolls the die and if it comes up a 4, a sample is taken of that meat. Forty sides of beef are available for possible inspection. Define random variable x = number of sides selected for inspection out of the 40 available.
a)What is the mean of the random variable x?
b)What is the standard deviation of the random variable x?
a)What is the mean of the random variable x?
b)What is the standard deviation of the random variable x?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
42
While playing Monopoly, Laura estimated the probabilities of the non-zero rents according to the following probability distribution:  Consider the random variable x = dollar amount in rent in a Monopoly roll.
Consider the random variable x = dollar amount in rent in a Monopoly roll.
a)If the table above specifies the probability distribution f(x), what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?
 Consider the random variable x = dollar amount in rent in a Monopoly roll.
Consider the random variable x = dollar amount in rent in a Monopoly roll.a)If the table above specifies the probability distribution f(x), what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
43
Let z denote a random variable having a standard normal distribution. Determine each of the following probabilities.
a)P(z < 1.36)
b)P(z < −2.05)
c)P(z > −1.15)
d)P(−1.10 < z < 2.54)
a)P(z < 1.36)
b)P(z < −2.05)
c)P(z > −1.15)
d)P(−1.10 < z < 2.54)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
44
For a variable z that has a standard normal distribution,
a)What is the probability that z < −2.45?
b)What is the probability that z < +1.67?
c)What is the probability that z is between −1.43 and +1.43?
d)What value of z separates the smaller 10% of the standard normal distribution from the larger 90%?
e)What values of −z and +z separate the middle 95% of the standard normal distribution from the extreme 5%?
a)What is the probability that z < −2.45?
b)What is the probability that z < +1.67?
c)What is the probability that z is between −1.43 and +1.43?
d)What value of z separates the smaller 10% of the standard normal distribution from the larger 90%?
e)What values of −z and +z separate the middle 95% of the standard normal distribution from the extreme 5%?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
45
Determine the following areas under the standard normal (z) curve.
a)The area under the z curve to the left of 1.56
b)The area under the z curve to the left of −2.13
c)The area under the z curve to the right of 0.88
d)The area under the z curve to the right of −1.23
e)The area under the z curve between −2 and 3
f)The area under the z curve between −2.4 and −1.4
a)The area under the z curve to the left of 1.56
b)The area under the z curve to the left of −2.13
c)The area under the z curve to the right of 0.88
d)The area under the z curve to the right of −1.23
e)The area under the z curve between −2 and 3
f)The area under the z curve between −2.4 and −1.4

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
46
The owners of the Burger Emporium are looking for new supplier of onions for their famous hamburgers. It is important that the onion slice be roughly the same diameter as the hamburger patty. After careful analysis, they determine that they can only use onions with diameters between 9 and 10 cm. Company A provides onions with diameters that are approximately normally distributed with mean 10.3 cm and standard deviation of 1.2 cm. Company B provides onions with diameters that are approximately normally distributed with mean 10.6 cm and standard deviation of 0.9 cm. Which company provides the higher proportion of usable onions? Justify your choice with an appropriate statistical argument.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
47
At a large university students have either a final exam or a final paper at the end of a course. The table below lists the distribution of the number of final exams that students at the university will take, and their associated probabilities. What are the mean and standard deviation of this distribution? 


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
48
Let z denote a random variable having a standard normal distribution. Determine each of the following probabilities.
a)P(z < 1.28)
b)P(z < −1.05)
c)P(z > −2.51)
d)P(−1.30 < z < 1.54)
a)P(z < 1.28)
b)P(z < −1.05)
c)P(z > −2.51)
d)P(−1.30 < z < 1.54)

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
49
In the old Roman Coliseum, two horses would be placed in tandem (side by side) and hitched to a chariot. Since the fast chariots needed to be able to pass the slow chariots, it was of some importance that the horses have room to run, but also they should not be too large. For chariot hitching purposes, the widest measure across a horse occurs in the rump area. The mean rump width is approximately 27" with a standard deviation of about 2". Let random variable w = width in inches across the rump of a randomly selected horse
a)The usual length measure as it applies to horses is the "hand," which is by definition equal to 4". Define random variable h = width in hands across the rump of a randomly selected horse. What are the mean and standard deviation of h?
b)Suppose horses are randomly chosen for a particular Roman chariot. Define random variable c = h1 + h2 to be the rump width of two randomly selected horses. What are the mean and standard deviation of c?
c)Suppose that in the original chariot design a 16 inch separation of the horses is specified so that the horses have room to avoid each other. This leads to random variable a = 16 + w1 + w2. Describe how this addition of 16 inches of "wiggle room" would change the mean and standard deviation in part (b). Do not recalculate the mean and standard deviation.
a)The usual length measure as it applies to horses is the "hand," which is by definition equal to 4". Define random variable h = width in hands across the rump of a randomly selected horse. What are the mean and standard deviation of h?
b)Suppose horses are randomly chosen for a particular Roman chariot. Define random variable c = h1 + h2 to be the rump width of two randomly selected horses. What are the mean and standard deviation of c?
c)Suppose that in the original chariot design a 16 inch separation of the horses is specified so that the horses have room to avoid each other. This leads to random variable a = 16 + w1 + w2. Describe how this addition of 16 inches of "wiggle room" would change the mean and standard deviation in part (b). Do not recalculate the mean and standard deviation.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose that the maximum daily temperature in Hacienda Heights, CA, for the month of December has a mean of 17°Celsius with a standard deviation of 3°Celsius. Let F be the random variable maximum daily temperature in degrees Fahrenheit. (Degrees 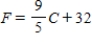 .)a)What is the mean of F?
.)a)What is the mean of F?
b)What is the standard deviation of F?
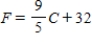 .)a)What is the mean of F?
.)a)What is the mean of F?b)What is the standard deviation of F?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
51
The owners of the Burger Emporium are looking for new supplier of tomatoes for their famous hamburgers. It is important that the tomato slice be roughly the same diameter as the hamburger patty. After careful analysis, they determine that they can only use tomatoes with diameters between 9 and 10 cm. Company A provides tomatoes with diameters that are approximately normally distributed with mean 10.5 cm and standard deviation of 1.1 cm. Company B provides tomatoes with diameters that are approximately normally distributed with mean 10.3 cm and standard deviation of 0.8 cm. Which company provides the higher proportion of usable tomatoes? Justify your choice with an appropriate statistical argument.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
52
In the somewhat less than towering ski slopes of northeastern Iowa new skiers come to learn to ski. On Big Bunny Slope skiers will fail to make the turn at Big Bend. On Little Bunny Slope, skiers will sometimes tumble at Little Hill. The ski instructors send the new skiers down the two slopes in groups of 25, wait a few moments, and then send the Ski Patrol Ambulance down after them, stopping at Big Bend and then Little Hill. The skiers descend the slopes far enough apart that they don't run into each other, so their spills are all independent.
a)The probability that a random new skier in the group will need to be carried to the First Aid Station after a spill at Big Bend is 0.3. If we define the random variable B = number of new skiers needing to be driven to the First Aid Station from Big Bend, we can model this situation as a binomial chance experiment. What is the mean and standard deviation of B?
b)The probability that a random new skier in the group will need to be carried to the First Aid Station after a spill at Little Hill is 0.1. If we define the random variable L = number of new skiers needing to be driven to the First Aid Station from Little Hill, what is the mean and standard deviation of L?
c)The total number of injuries requiring the Ambulance, T, is a random variable formed by calculating B + L. What are the mean and standard deviation of the random variable T?
d)When the 25 skiers are sent down from the top of Big Bunny Slope, they are sent one at a time. What is the probability that the first one needing the Ambulance is the 7th one to be sent down the slope?
a)The probability that a random new skier in the group will need to be carried to the First Aid Station after a spill at Big Bend is 0.3. If we define the random variable B = number of new skiers needing to be driven to the First Aid Station from Big Bend, we can model this situation as a binomial chance experiment. What is the mean and standard deviation of B?
b)The probability that a random new skier in the group will need to be carried to the First Aid Station after a spill at Little Hill is 0.1. If we define the random variable L = number of new skiers needing to be driven to the First Aid Station from Little Hill, what is the mean and standard deviation of L?
c)The total number of injuries requiring the Ambulance, T, is a random variable formed by calculating B + L. What are the mean and standard deviation of the random variable T?
d)When the 25 skiers are sent down from the top of Big Bunny Slope, they are sent one at a time. What is the probability that the first one needing the Ambulance is the 7th one to be sent down the slope?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
53
When driving the nation's highways Anna is known as something of a lead foot. The number of miles per hour over the speed limit varies, but has a mean of 7.5 mph and standard deviation of 2 mph. Unfortunately, the state in which she goes to college adjusts the fines so that the amount of the fine is given by the formula:
F = 10(MPH) + 112,
where F is the amount of the fine, and MPH is the number of miles over the speed limit. Let random variable F be the amount of her fine if she is randomly stopped for speeding.
a)What is the mean of F?
b)What is the standard deviation of F?
F = 10(MPH) + 112,
where F is the amount of the fine, and MPH is the number of miles over the speed limit. Let random variable F be the amount of her fine if she is randomly stopped for speeding.
a)What is the mean of F?
b)What is the standard deviation of F?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
54
At the last home football game, the senior football players walk through a specially constructed welcoming arch, 2 abreast. It is considered unseemly to bump each other on the way through, so the arch must be wide enough for two players to go through. The distribution of widths of football players with shoulder pads on is approximately normal; the mean padded football player width is 30 inches, and the standard deviation is 5 inches. Let random variable w = width in inches of a randomly selected padded football player.
a)Since this is a statistics test, the carpenter who will be constructing the arch has only metric measuring tools, and must convert all the information above to metric measures. 1 inch = 2.54 centimeters, and we define random variable m = width in centimeters of a randomly selected padded football player. What are the mean and standard deviation of m?
b)Suppose the football players are paired randomly to go through the arch. Define random variable v = w1 + w2 to be the collective width (in inches) of two randomly selected football players. What are the mean and standard deviation of v?
c)Suppose that in the original specifications of the arch a 10 inch separation of the football players is specified so that the football players have room to avoid each other. This leads to random variable a = 10 + w1 + w2. Describe how this addition of 10 inches of "wiggle room" would change the mean and standard deviation in part (b). Do not recalculate the mean and standard deviation.
a)Since this is a statistics test, the carpenter who will be constructing the arch has only metric measuring tools, and must convert all the information above to metric measures. 1 inch = 2.54 centimeters, and we define random variable m = width in centimeters of a randomly selected padded football player. What are the mean and standard deviation of m?
b)Suppose the football players are paired randomly to go through the arch. Define random variable v = w1 + w2 to be the collective width (in inches) of two randomly selected football players. What are the mean and standard deviation of v?
c)Suppose that in the original specifications of the arch a 10 inch separation of the football players is specified so that the football players have room to avoid each other. This leads to random variable a = 10 + w1 + w2. Describe how this addition of 10 inches of "wiggle room" would change the mean and standard deviation in part (b). Do not recalculate the mean and standard deviation.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
55
While playing Monopoly, Andi estimated the probabilities of the non-zero rents according to the following probability distribution: 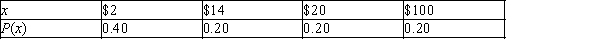 Consider the random variable x = dollar amount in rent collected in a Monopoly roll.
Consider the random variable x = dollar amount in rent collected in a Monopoly roll.
a)If the table above specifies the probability distribution of x, what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?
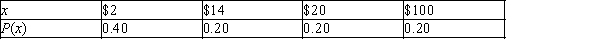 Consider the random variable x = dollar amount in rent collected in a Monopoly roll.
Consider the random variable x = dollar amount in rent collected in a Monopoly roll.a)If the table above specifies the probability distribution of x, what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
56
For a variable that has a standard normal distribution,
a)What is the probability that z < −1.34?
b)What is the probability that z < +2.56?
c)What is the probability that z is between −1.5 and +1.5.
d)What value of z separates the smaller 5% of the standard normal distribution from the larger 95%?
e)What values of −z and +z separate the middle 90% of the standard normal distribution from the extreme 10%?
a)What is the probability that z < −1.34?
b)What is the probability that z < +2.56?
c)What is the probability that z is between −1.5 and +1.5.
d)What value of z separates the smaller 5% of the standard normal distribution from the larger 95%?
e)What values of −z and +z separate the middle 90% of the standard normal distribution from the extreme 10%?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
57
A gasoline tank for a certain model car is designed to hold 12 gallons of gas. Suppose that the actual capacity of the gas tank in cars of this type is well approximated by a normal distribution with mean 12.0 gallons and standard deviation 0.2 gallons. What is the probability that a randomly selected car of this model will have a gas tank that holds at most 11.7 gallons?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
58
Determine the following areas under the standard normal (z) curve.
a)The area under the z curve to the left of 2.53
b)The area under the z curve to the left of −1.33
c)The area under the z curve to the right of 0.76
d)The area under the z curve to the right of −1.47
e)The area under the z curve between −1 and 3
f)The area under the z curve between −2.6 and −1.2
a)The area under the z curve to the left of 2.53
b)The area under the z curve to the left of −1.33
c)The area under the z curve to the right of 0.76
d)The area under the z curve to the right of −1.47
e)The area under the z curve between −1 and 3
f)The area under the z curve between −2.6 and −1.2

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
59
A State Dept. of Education is writing a state-wide math test, and by law must decide how many points will count as a "failing score." The test consists of 50 True/False questions and 40 multiple choice questions with 5 answer options. The total score (TS) will be equal to the number of true/false items correct plus twice the number of multiple-choice items correct. A decision has been made to make the failing score the score that a student would be expected to get if they randomly guessed on all the questions.
a)If a student is randomly guessing, the 50 True/False questions can be regarded as a binomial chance experiment with probability of success equal to 0.50. If we define the random variable T = score from T/F items, what are the mean and standard deviation of T for a random student who is guessing?
b)If a student is randomly guessing, the 40 multiple choice questions can be regarded as a binomial chance experiment with probability of success equal to 0.20. If we define the random variable M = score from MC items, what are the mean and standard deviation of the M for a random student who is guessing?
c)The total score, TS, is a random variable formed by calculating T + 2M. What are the mean and standard deviation of the random variable TS?
d)If a student is randomly guessing on the multiple choice part of the test, what is the probability that the first multiple choice question correct is the 4th multiple choice question?
a)If a student is randomly guessing, the 50 True/False questions can be regarded as a binomial chance experiment with probability of success equal to 0.50. If we define the random variable T = score from T/F items, what are the mean and standard deviation of T for a random student who is guessing?
b)If a student is randomly guessing, the 40 multiple choice questions can be regarded as a binomial chance experiment with probability of success equal to 0.20. If we define the random variable M = score from MC items, what are the mean and standard deviation of the M for a random student who is guessing?
c)The total score, TS, is a random variable formed by calculating T + 2M. What are the mean and standard deviation of the random variable TS?
d)If a student is randomly guessing on the multiple choice part of the test, what is the probability that the first multiple choice question correct is the 4th multiple choice question?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
60
When planning for the big Statistics Department Super Bowl party, it is sometimes not clear what kinds of chips that people will want to have available, nor is it clear how many people will actually show up at the party. Because of this Professor Mean takes a 4-sided die to the grocery store, starts at one end of the chips aisle, and travels to the other end. At each different kind of chips, Dr. Mean rolls the die. If it comes up a 4, she purchases the chips for the party. There are 40 different kinds of chips in the aisle. Define random variable x = number of types of chips purchased out of 40.
a)What is the mean of the random variable x?
b)What is the standard deviation of the random variable x?
a)What is the mean of the random variable x?
b)What is the standard deviation of the random variable x?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
61
In a study of the reaction times of left- and right-handers' reaction times to tones delivered to the right ear, the right-handers' scores were approximately normally distributed with a mean of 210 milliseconds and standard deviation of 40 milliseconds. The mean score for left-handers was 240 ms.
a)Sketch a normal distribution that describes right-handers' reaction times, and locate the mean reaction time for left-handers in this distribution.
b)About what proportion of right-handers reaction times would be "better" (i.e. smaller) than the mean reaction time for left-handers?
a)Sketch a normal distribution that describes right-handers' reaction times, and locate the mean reaction time for left-handers in this distribution.
b)About what proportion of right-handers reaction times would be "better" (i.e. smaller) than the mean reaction time for left-handers?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
62
In a study of the reaction times of left- and right-handers' reaction times to tones delivered to the right ear, the right-handers' scores were approximately normally distributed with a mean of 240 milliseconds and standard deviation of 32 milliseconds. The mean score for right-handers was 210 ms.
a)Sketch a normal distribution that describes left-handers' reaction times, and locate the mean reaction time for right-handers in this distribution.
b)About what proportion of left-handers reaction times would be "better" (i.e. smaller) than the mean reaction time for right-handers?
a)Sketch a normal distribution that describes left-handers' reaction times, and locate the mean reaction time for right-handers in this distribution.
b)About what proportion of left-handers reaction times would be "better" (i.e. smaller) than the mean reaction time for right-handers?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
63
Seventy-five percent of the computers sold by a certain store are laptops. Among 150 randomly selected computer purchases, what is the approximate probability that at most 125 are laptops? What is the approximate probability that between 100 and 120 (inclusive) are laptops?
A)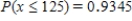 ;
; 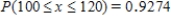 .
.
B)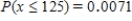 ;
; 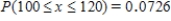 .
.
C)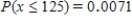 ;
; 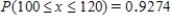 .
.
D)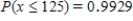 ;
; 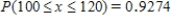 .
.
E)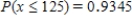 ;
; 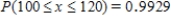 .
.
A)
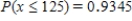 ;
; 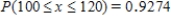 .
.B)
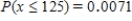 ;
; 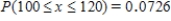 .
.C)
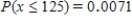 ;
; 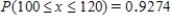 .
.D)
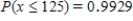 ;
; 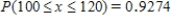 .
.E)
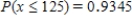 ;
; 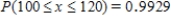 .
.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
64
Suppose that in a certain metropolitan area 18% of all automobiles are equipped with an electric engine. Let  denote the number among of 9 randomly selected automobiles that are equipped with an electric engine. Calculate
denote the number among of 9 randomly selected automobiles that are equipped with an electric engine. Calculate 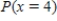 . Let the random variable
. Let the random variable  denote the number of passing automobiles that are equipped with an electric engine until you find automobile with another type of engine. Calculate
denote the number of passing automobiles that are equipped with an electric engine until you find automobile with another type of engine. Calculate 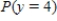 .
.
A)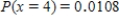 ,
, 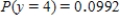
B)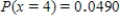 ,
, 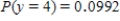
C)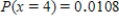 ,
, 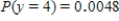
D)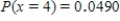 ,
, 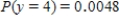
E)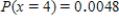 ,
, 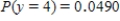
 denote the number among of 9 randomly selected automobiles that are equipped with an electric engine. Calculate
denote the number among of 9 randomly selected automobiles that are equipped with an electric engine. Calculate 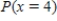 . Let the random variable
. Let the random variable  denote the number of passing automobiles that are equipped with an electric engine until you find automobile with another type of engine. Calculate
denote the number of passing automobiles that are equipped with an electric engine until you find automobile with another type of engine. Calculate 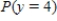 .
. A)
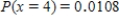 ,
, 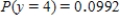
B)
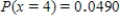 ,
, 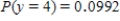
C)
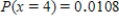 ,
, 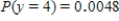
D)
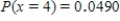 ,
, 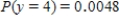
E)
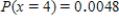 ,
, 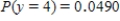

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
65
Suppose that the random variable 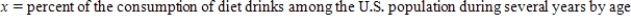 has the probability distribution described by the following density curve.
has the probability distribution described by the following density curve. 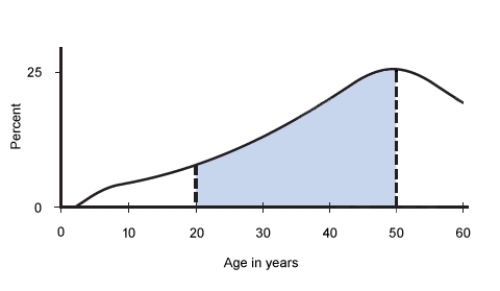
What probability is represented by the shaded area? Suppose the shaded area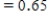 . Interpret this probability in the context of this problem.
. Interpret this probability in the context of this problem.
A)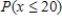 .About 65% of U.S.population consuming diet drinks are people aged less than 20 years.
.About 65% of U.S.population consuming diet drinks are people aged less than 20 years.
B)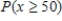 .About 65% of U.S.population consuming diet drinks are people aged 50 years and over.
.About 65% of U.S.population consuming diet drinks are people aged 50 years and over.
C)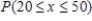 .About 65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
.About 65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
D)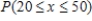 .About 0.65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
.About 0.65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
E)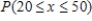 .About 35% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
.About 35% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
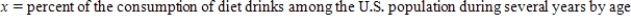 has the probability distribution described by the following density curve.
has the probability distribution described by the following density curve. 
What probability is represented by the shaded area? Suppose the shaded area
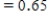 . Interpret this probability in the context of this problem.
. Interpret this probability in the context of this problem.A)
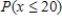 .About 65% of U.S.population consuming diet drinks are people aged less than 20 years.
.About 65% of U.S.population consuming diet drinks are people aged less than 20 years.B)
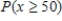 .About 65% of U.S.population consuming diet drinks are people aged 50 years and over.
.About 65% of U.S.population consuming diet drinks are people aged 50 years and over.C)
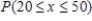 .About 65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
.About 65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.D)
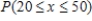 .About 0.65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
.About 0.65% of U.S.population consuming diet drinks are people aged between 20 and 50 years.E)
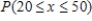 .About 35% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
.About 35% of U.S.population consuming diet drinks are people aged between 20 and 50 years.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
66
Ron rolls a six-sided dice until the number six is shown. What is the probability that he rolls a dice at least three times? What is the probability that he rolls a dice at most four times?
A)0.3056; 0.5177.
B)0.3056; 0.4823.
C)0.6944; 0.5177.
D)0.6944; 0.4823.
E)0.5787; 0.4213.
A)0.3056; 0.5177.
B)0.3056; 0.4823.
C)0.6944; 0.5177.
D)0.6944; 0.4823.
E)0.5787; 0.4213.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
67
The graphs below are normal probability plots of the vocabulary and math concept scores on a standardized exam for a large sample of students. One of the score distributions is approximately normal. Identify the score distribution that is approximately normal and explain the reason for your choice.
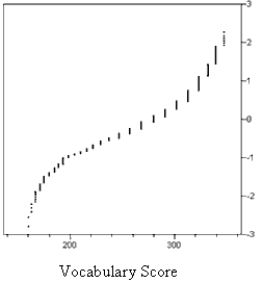
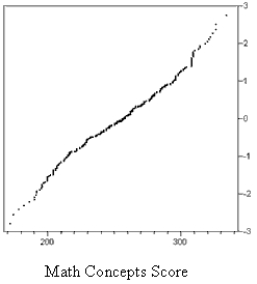



Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
68
Briefly describe how one would decide which of two transformations was better for transforming skewed data to obtain a distribution that was approximately normal.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
69
The time that it takes a randomly selected employee to perform a certain task is approximately normally distributed with a mean value of 120 seconds and a standard deviation of 20 seconds. The slowest 10% (that is, the 10% with the longest times) are to be given remedial training. What times qualify for the remedial training?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
70
Suppose that 73% of the visitors to a certain barbershop have a beard. Let the random variable x denote the number of coming visitors that have a beard until the visitor without beard comes. What is the probability that at most three visitors with beard must come? What is the probability that more than five visitors with beard must come?
A)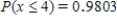 ;
; 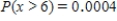
B)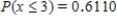 ;
; 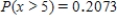
C)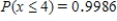 ;
; 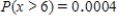
D)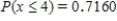 ;
; 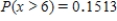
E)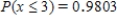 ;
; 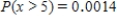
A)
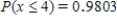 ;
; 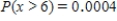
B)
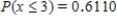 ;
; 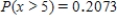
C)
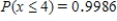 ;
; 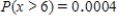
D)
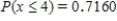 ;
; 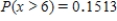
E)
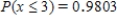 ;
; 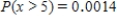

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
71
Briefly describe how the correlation coefficient can be used to check for normality.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
72
Suppose that call-center receives on average 1.7 calls per minute. The graphs below show the probability of receiving calls. Determine the distribution curve with the shaded region that corresponds to the probability of the event that call happens between two and six minutes. Chose the correct graph.
A)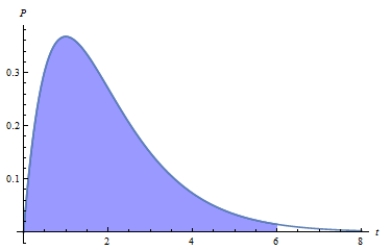
B)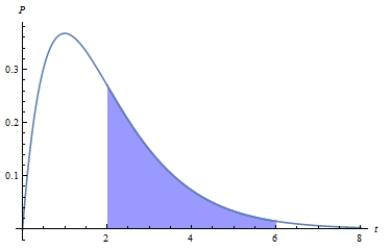
C)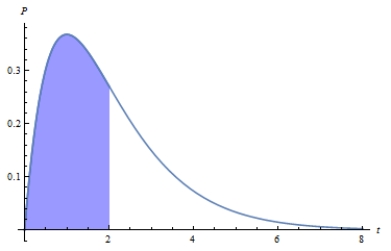
D)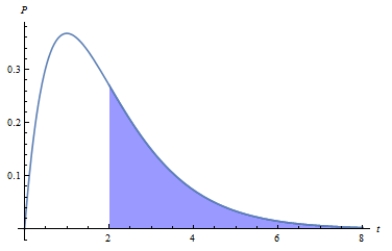
E)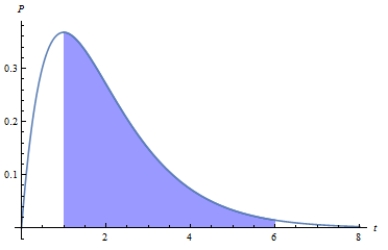
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck


