Exam 6: Random Variables and Probability Distributions
Exam 1: Collecting Data in Reasonable Ways56 Questions
Exam 2: Graphical Methods for Describing Data Distributions62 Questions
Exam 3: Numerical Methods for Describing Data Distributions37 Questions
Exam 4: Describing Bivariate Numerical Data70 Questions
Exam 5: Probability55 Questions
Exam 6: Random Variables and Probability Distributions72 Questions
Exam 7: An Overview of Statistical Inference - Learning From Data19 Questions
Exam 8: Sampling Variability and Sampling Distributions35 Questions
Exam 9: Estimating a Population Proportion36 Questions
Exam 10: Asking and Answering Questions About a Population Proportion31 Questions
Exam 11: Asking and Answering Questions About the Difference Between Two Proportions42 Questions
Exam 12: Asking and Answering Questions About a Population Mean51 Questions
Exam 13: Asking and Answering Questions About the Difference Between Two Means46 Questions
Exam 14: Learning From Categorical Data36 Questions
Exam 15: Understanding Relationships - Numerical Data Part 243 Questions
Exam 16: Asking and Answering Questions About More Than Two Means25 Questions
Select questions type
Inspecting meat is a very important part of the process of ensuring healthy food. So that meat inspectors do not fall into a pattern of inspection, they use a 4-sided die to decide whether or not to sample the meat from a particular "side" of beef. The meat inspector rolls the die and if it comes up a 4, a sample is taken of that meat. Forty sides of beef are available for possible inspection. Define random variable x = number of sides selected for inspection out of the 40 available.
a)What is the mean of the random variable x?
b)What is the standard deviation of the random variable x?
Free
(Essay)
4.9/5  (39)
(39)
Correct Answer:
a)mean: 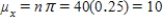 b)standard deviation:
b)standard deviation: 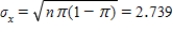
For a continuous random variable x, the height of the density curve over an interval a to b represents the probability that x is between a and b.
Free
(True/False)
4.8/5  (28)
(28)
Correct Answer:
False
When planning for the big Statistics Department Super Bowl party, it is sometimes not clear what kinds of chips that people will want to have available, nor is it clear how many people will actually show up at the party. Because of this Professor Mean takes a 4-sided die to the grocery store, starts at one end of the chips aisle, and travels to the other end. At each different kind of chips, Dr. Mean rolls the die. If it comes up a 4, she purchases the chips for the party. There are 40 different kinds of chips in the aisle. Define random variable x = number of types of chips purchased out of 40.
a)What is the mean of the random variable x?
b)What is the standard deviation of the random variable x?
Free
(Essay)
4.8/5  (44)
(44)
Correct Answer:
a)mean: 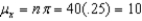
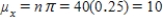
b)standard deviation: 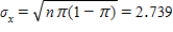
A chemical supply company currently has in stock 100 pounds of a certain chemical, which it sells to customers in 5-pound lots. Let 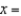 the number of lots ordered by a randomly chosen customer. The probability distribution of x is as follows:
the number of lots ordered by a randomly chosen customer. The probability distribution of x is as follows:  Calculate the mean value of x.
Calculate the mean value of x.
(Multiple Choice)
4.9/5  (45)
(45)
While playing Monopoly, Laura estimated the probabilities of the non-zero rents according to the following probability distribution:  Consider the random variable x = dollar amount in rent in a Monopoly roll.
a)If the table above specifies the probability distribution f(x), what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?
Consider the random variable x = dollar amount in rent in a Monopoly roll.
a)If the table above specifies the probability distribution f(x), what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?
(Essay)
4.8/5  (35)
(35)
A random variable is discrete if the value of the random variable depends upon the outcome of a chance experiment.
(True/False)
5.0/5  (40)
(40)
For a variable that has a standard normal distribution,
a)What is the probability that z < −1.34?
b)What is the probability that z < +2.56?
c)What is the probability that z is between −1.5 and +1.5.
d)What value of z separates the smaller 5% of the standard normal distribution from the larger 95%?
e)What values of −z and +z separate the middle 90% of the standard normal distribution from the extreme 10%?
(Essay)
4.8/5  (32)
(32)
The owners of the Burger Emporium are looking for new supplier of tomatoes for their famous hamburgers. It is important that the tomato slice be roughly the same diameter as the hamburger patty. After careful analysis, they determine that they can only use tomatoes with diameters between 9 and 10 cm. Company A provides tomatoes with diameters that are approximately normally distributed with mean 10.5 cm and standard deviation of 1.1 cm. Company B provides tomatoes with diameters that are approximately normally distributed with mean 10.3 cm and standard deviation of 0.8 cm. Which company provides the higher proportion of usable tomatoes? Justify your choice with an appropriate statistical argument.
(Essay)
4.8/5  (38)
(38)
At the last home football game, the senior football players walk through a specially constructed welcoming arch, 2 abreast. It is considered unseemly to bump each other on the way through, so the arch must be wide enough for two players to go through. The distribution of widths of football players with shoulder pads on is approximately normal; the mean padded football player width is 30 inches, and the standard deviation is 5 inches. Let random variable w = width in inches of a randomly selected padded football player.
a)Since this is a statistics test, the carpenter who will be constructing the arch has only metric measuring tools, and must convert all the information above to metric measures. 1 inch = 2.54 centimeters, and we define random variable m = width in centimeters of a randomly selected padded football player. What are the mean and standard deviation of m?
b)Suppose the football players are paired randomly to go through the arch. Define random variable v = w1 + w2 to be the collective width (in inches) of two randomly selected football players. What are the mean and standard deviation of v?
c)Suppose that in the original specifications of the arch a 10 inch separation of the football players is specified so that the football players have room to avoid each other. This leads to random variable a = 10 + w1 + w2. Describe how this addition of 10 inches of "wiggle room" would change the mean and standard deviation in part (b). Do not recalculate the mean and standard deviation.
(Essay)
4.7/5  (39)
(39)
Suppose that call-center receives on average 1.7 calls per minute. The graphs below show the probability of receiving calls. Determine the distribution curve with the shaded region that corresponds to the probability of the event that call happens between two and six minutes. Chose the correct graph.
(Multiple Choice)
4.9/5  (32)
(32)
Thirty-seven percent of the customers of a grocery store use an express checkout. Consider four randomly selected customers, and let x denote the number among the four who use the express checkout.
Calculate 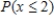 .
.
(Multiple Choice)
4.8/5  (39)
(39)
A random variable is continuous if the set of possible values includes an entire interval on the number line.
(True/False)
4.8/5  (30)
(30)
While playing Monopoly, Andi estimated the probabilities of the non-zero rents according to the following probability distribution: 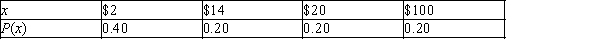 Consider the random variable x = dollar amount in rent collected in a Monopoly roll.
a)If the table above specifies the probability distribution of x, what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?
Consider the random variable x = dollar amount in rent collected in a Monopoly roll.
a)If the table above specifies the probability distribution of x, what is the mean of the random variable x?
b)If the probabilities are associated with the outcomes as in the table above, what is the standard deviation of the random variable x?
(Essay)
4.8/5  (47)
(47)
From your own experience, give an example of a continuous random variable and a discrete random variable. In a few sentences, explain why each is categorized as continuous or discrete.
(Essay)
5.0/5  (26)
(26)
At the College of Warm & Fuzzy, good grades in math are very easy to come by. The grade distribution is given in the table below:  Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
a)BAC
b)CFF
c)ABA
Suppose three students are to be selected at random. As each is selected their math grades are written down and they are replaced back into the population of students. Three possible outcomes of this experiment are listed below. Calculate the probabilities of these sequences appearing.
a)BAC
b)CFF
c)ABA
(Essay)
4.9/5  (38)
(38)
The density curve for a continuous random variable is shown below. Use this curve to find the following probabilities:
a)P(x < 1)b)P(2 < x < 3)c)P(x is at least 3) 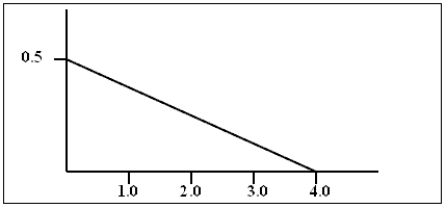 You may use the following area formulas in your calculations:
Area of a rectangle:
A = lw
Area of a trapezoid:
You may use the following area formulas in your calculations:
Area of a rectangle:
A = lw
Area of a trapezoid: 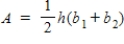 Area of a right triangle:
Area of a right triangle: 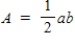
(Essay)
4.8/5  (36)
(36)
Which of the following random variables are continuous? I). the air pressure in an automobile tire (in pounds per square inch)II). the diameter of an automobile tire (in centimeters)III). the number of miles traveled by an automobile tire
(Multiple Choice)
4.9/5  (38)
(38)
Showing 1 - 20 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)