Deck 5: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/55
Play
Full screen (f)
Deck 5: Probability
1
Suppose you want to estimate the probability that a randomly selected customer at a particular grocery store will pay by credit card. Over the past 3 months, 70,600 purchases were made, and 22,200 of them were paid for by credit card. What is the estimated probability that a randomly selected customer will pay by credit card?
A)0.3144
B)0.5391
C)0.7233
D)0.8548
E)0.8633
A)0.3144
B)0.5391
C)0.7233
D)0.8548
E)0.8633
0.3144
2
Two events are independent if they cannot occur simultaneously.
False
3
The event "A or B " consists of all of the outcomes in both of the events.
False
4
If two events, A and B, are mutually exclusive, then 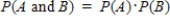 .
.
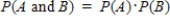 .
.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
5
An event consisting of exactly one outcome is called a simple event.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
6
Each time a class meets, the professor selects one student at random to explain the solution to a homework problem. There are 60 students in the class, and no one ever misses class. Luke is one of these students. What is the probability that Luke is selected both of the next two times that the class meets?
A)0.00028
B)0.03333
C)0.5
D)0.01724
E)0.00015
A)0.00028
B)0.03333
C)0.5
D)0.01724
E)0.00015

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
7
Any collection of possible outcomes of a chance experiment is called a sample space.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
8
The General Multiplication Rule states that 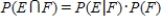 .
.
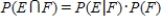 .
.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
9
The General Addition Rule states that 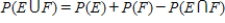
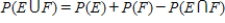

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
10
The classical view of probability is based on the Law of Large Numbers.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
11
Two events, E and F, are independent if 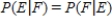 .
.
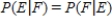 .
.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
12
An airline reports that for a particular flight operating daily between Phoenix and Atlanta, the probability of an on-time arrival is 0.64. Give a relative frequency interpretation of this probability.
A)In the long run, 0.64% of the time this particular flight that flies between Phoenix and Atlanta will arrive on time.
B)In the long run, 36% of the time this particular flight that flies between Phoenix and Atlanta will arrive on time.
C)In the long run, 64% of the time this particular flight that flies between Phoenix and Atlanta will arrive on time.
D)In the long run, 64% of the time this particular flight that flies between Phoenix and Atlanta will not arrive on time.
E)In the long run, 64% of the time this particular flight that flies between Phoenix and Atlanta will arrive earlier than expected.
A)In the long run, 0.64% of the time this particular flight that flies between Phoenix and Atlanta will arrive on time.
B)In the long run, 36% of the time this particular flight that flies between Phoenix and Atlanta will arrive on time.
C)In the long run, 64% of the time this particular flight that flies between Phoenix and Atlanta will arrive on time.
D)In the long run, 64% of the time this particular flight that flies between Phoenix and Atlanta will not arrive on time.
E)In the long run, 64% of the time this particular flight that flies between Phoenix and Atlanta will arrive earlier than expected.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose you want to estimate the probability that a patient will develop an infection while hospitalized at a particular hospital. In the past year, this hospital had 8,650 patients, and 812 of them developed an infection. What is the estimated probability that a patient at this hospital will develop an infection?
A)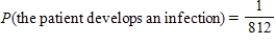
B)
C)
D)
E)
A)
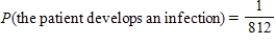
B)

C)

D)

E)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
14
A large cable company reports that 70% of its customers subscribe to its cable TV service, 32% subscribe to its Internet service, and 87% subscribe to at least one of these two services. Use the given probability information to select a "hypothetical 1000" table.
A)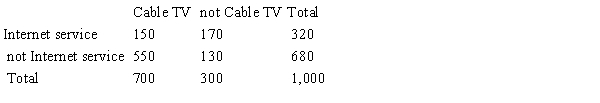
B)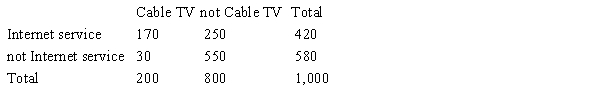
C)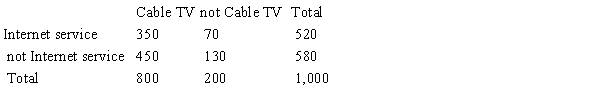
D)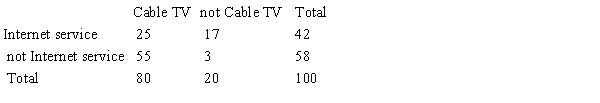
E)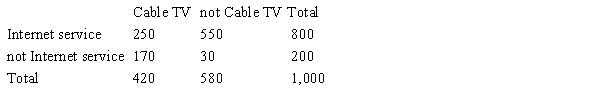
A)
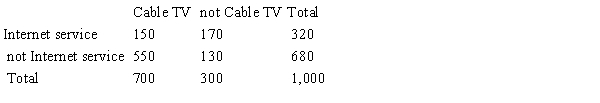
B)
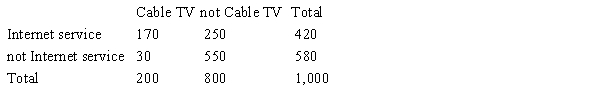
C)
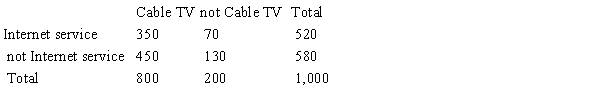
D)
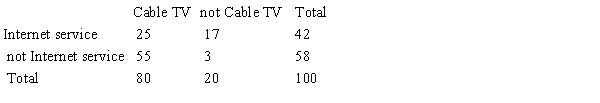
E)
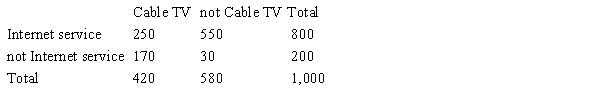

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
15
Two events are said to be disjoint or mutually exclusive when they have no outcomes in common.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
16
A rental car company offers two options when a car is rented. A renter can choose to pre-purchase gas or not and can also choose to rent a GPS device or not. Suppose that the events
A = event that gas is pre-purchased
B = event that a GPS is rented
Are independent with P(A) = 0.35 and P(B) = 0.50.
Select a "hypothetical 1000" table with columns corresponding to whether or not gas is pre-purchased and rows corresponding to whether or not a GPS is rented.
A)
B)
C)
D)
E)
A = event that gas is pre-purchased
B = event that a GPS is rented
Are independent with P(A) = 0.35 and P(B) = 0.50.
Select a "hypothetical 1000" table with columns corresponding to whether or not gas is pre-purchased and rows corresponding to whether or not a GPS is rented.
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
17
A deck of 52 cards is mixed well, and 5 cards are dealt. It can be shown that (disregarding the order in which the cards are dealt) there are 2,598,960 possible hands, of which only 4 hands are royal flushes. (A royal flush is a hand consisting of 10, J, Q, K, and A, all of the same suit).
What is the probability that a hand will be a royal flush?
A)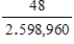
B)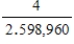
C)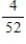
D)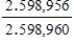
E)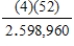
What is the probability that a hand will be a royal flush?
A)
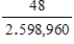
B)
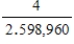
C)
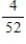
D)
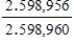
E)
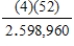

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
18
The faces of a twelve-sided die are numbered with the numbers 1 through 12. If you roll this die 600 times, how many nines do you expect to roll?
A)about 67
B)about 50
C)about 60
D)about 100
E)none
A)about 67
B)about 50
C)about 60
D)about 100
E)none

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
19
A chance experiment is any activity or situation in which there is uncertainty concerning which of two or more possible outcomes will result.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
20
The probability of an event E can always be computed using the formula,



Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
21
Investigators recently reported the results a study designed to assess whether or not the herb, St. John's Wort is effective in treating moderately severe cases of depression. The study involved 338 subjects, randomly assigned to receive one of three treatments: St. John's Wort , Zoloft, or a placebo. The authors were primarily interested in whether St. John's Wort performed better than placebo and included Zoloft as a "way to measure how sensitive the trial was to detecting antidepressant effects." Their results are presented in the table below. 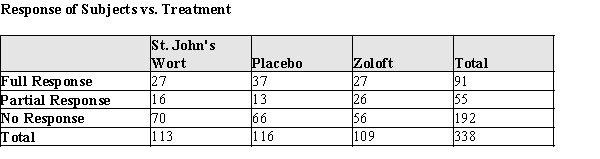
a)What is the probability that a randomly selected subject had no response?
b)What is the probability that a randomly selected subject was treated with Zoloft and had a full response?
c)What is the probability that a randomly selected subject had a full or partial response given that they were treated with St. John's Wort?
d)What is the probability that a randomly selected subject that didn't have a full response was treated with Placebo?

a)What is the probability that a randomly selected subject had no response?
b)What is the probability that a randomly selected subject was treated with Zoloft and had a full response?
c)What is the probability that a randomly selected subject had a full or partial response given that they were treated with St. John's Wort?
d)What is the probability that a randomly selected subject that didn't have a full response was treated with Placebo?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
22
The football team at North Snowshoe High is in a little bit of trouble. Two of their players have just left the game with injuries, and due to the flu the coach only has 5 players to choose from: three linemen, a quarterback, and the punter who doubles as the team statistician. The coach must choose two of those five to go into the game. Unfortunately, it is snowing very severely, making it difficult for the coach to see the players on the bench. Therefore he randomly selects two players to go into the game. (He CAN tell there are two players, so of course he sends them in without replacement!) What is the probability that the team statistician will be selected?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
23
Students in two classes of upper-level mathematics were classified according to class standing and gender, resulting in the following table.  Define events A, B, and C as follows:
Define events A, B, and C as follows:
A = the event that the selected student is a female
B = the event that the selected student is a male
C = the event that the selected student is a senior.
In the following table indicate by putting an X in the appropriate cells which is true for each pair of events.
X = Yes, Blank = No
 Define events A, B, and C as follows:
Define events A, B, and C as follows:A = the event that the selected student is a female
B = the event that the selected student is a male
C = the event that the selected student is a senior.
In the following table indicate by putting an X in the appropriate cells which is true for each pair of events.
X = Yes, Blank = No


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose that 70% of the orders on a particular website are shipped to the person who is making the order and the remaining 30% are shipped to people other than the person placing the order. Gift wrapping is requested for 60% of the orders being shipped to other people, but for only 10% of orders shipped to the person making the order.
a)What is the probability that a randomly selected order will be gift wrapped and sent to another person?
b)What is the probability that a randomly selected order will be gift wrapped?
c)Is gift wrapping independent of the destination of the gift? Justify your response statistically.
a)What is the probability that a randomly selected order will be gift wrapped and sent to another person?
b)What is the probability that a randomly selected order will be gift wrapped?
c)Is gift wrapping independent of the destination of the gift? Justify your response statistically.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
25
Experimental studies utilize blinding to prevent researchers from biasing their measurements of the patients. But can they guess the treatment? In a study of a psychotherapeutic intervention, clinicians who were blinded were asked to guess what treatment their patients received. Data from that experiment are shown below. Assume that these data are indicative of the population of these treatments. 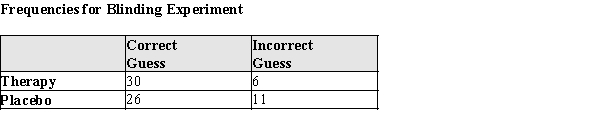
a)What is the probability that a correct guess is made for a randomly chosen subject?
b)If a randomly chosen subject received the placebo, what is the probability that the researcher correctly guesses the treatment?

a)What is the probability that a correct guess is made for a randomly chosen subject?
b)If a randomly chosen subject received the placebo, what is the probability that the researcher correctly guesses the treatment?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
26
Each of 400 people who purchased a Honda Civic was classified according to gender and whether the car purchased had a hybrid engine or not.  Find P (hybrid | male).
Find P (hybrid | male).
A)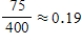
B)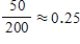
C)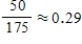
D)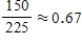
E)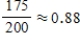
 Find P (hybrid | male).
Find P (hybrid | male).A)
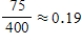
B)
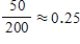
C)
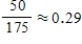
D)
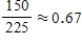
E)
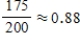

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
27
A statistics class conducts a chance experiment in which they observe students who buy a snack and the school vending machines. The type of food (Liquid, or Solid) is noted, as well as the number of calories of fat content (25, 50, or 75).
Let L be the event that the item is liquid and B be the event that the item has fewer than 75 calories of fat.
a)What outcomes are in BC?
b)What outcomes are in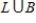 ?
?
c)What outcomes are in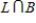 ?
?
Let L be the event that the item is liquid and B be the event that the item has fewer than 75 calories of fat.
a)What outcomes are in BC?
b)What outcomes are in
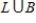 ?
?c)What outcomes are in
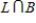 ?
?
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
28
In order to ensure the safety of school classrooms the local Fire Marshall does an inspection at Thomas Jefferson High School every month, looking for faulty wiring, overloaded circuits, etc. At TJHS the new Academic Wing has 5 math rooms, 10 science rooms, and 10 English rooms. The science rooms are divided into 8 biology and 2 chemistry rooms. Each month, the Fire Marshall randomly picks one of the rooms in the new wing to inspect each month. Define the following events:
S = the event the selected room is a science room
B = the event the selected room is a biology room
M = the event the selected room is a math room
E = the event the selected room is an English room
C = the event the selected room is a chemistry room
Calculate the probabilities of the events described below:
a)P(S)b)P(M or E )c)P(E or B)d)P(S and not C)
S = the event the selected room is a science room
B = the event the selected room is a biology room
M = the event the selected room is a math room
E = the event the selected room is an English room
C = the event the selected room is a chemistry room
Calculate the probabilities of the events described below:
a)P(S)b)P(M or E )c)P(E or B)d)P(S and not C)

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
29
The basketball team at North Snowshoe High is in a little bit of trouble. Two of their players have just fouled out on technicals, and due to the flu the coach only has 4 players to choose from: three forwards and a guard who doubles as the team statistician. In his haste, the coach will randomly choose two of the four to go into the game, and of course will do so without replacement. What is the probability that the team statistician will be selected?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
30
In a few sentences, explain the difference between conditional probability and "ordinary" (unconditional) probability.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
31
As every Girl Scout knows, statistics teachers seriously love Girl Scout Cookies. The number of boxes of GS cookies statistics teachers order, like all important decisions made by statistics teachers, is determined by independent rolls of a 4-sided fair die. If a one appears, 6 boxes are ordered; if any other number appears, 2 boxes are ordered.
a)What is the probability that a statistics teacher places an order for 2 boxes of Girl Scout cookies?
b)What is the probability that with two independently chosen statistics teachers will each order 6 boxes each?
c)What is the probability that for two independently chosen statistics teachers the first will order 6 boxes and the second will order 2 boxes?
d)What is the probability that for two independently chosen statistics teachers exactly one will order 6 boxes?
a)What is the probability that a statistics teacher places an order for 2 boxes of Girl Scout cookies?
b)What is the probability that with two independently chosen statistics teachers will each order 6 boxes each?
c)What is the probability that for two independently chosen statistics teachers the first will order 6 boxes and the second will order 2 boxes?
d)What is the probability that for two independently chosen statistics teachers exactly one will order 6 boxes?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
32
In a few sentences, distinguish between the classical and relative frequency approaches to probability.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
33
At Beth & Mary's Ice Cream Emporium customers may choose to sprinkle toppings on their ice cream. The toppings are classified as either candy (C) or fruit (F) toppings. Consider the chance experiment where the choice of toppings--(C) or (F)--is recorded for each of the next two customers who order ice cream.
a)List all the events in the sample space.
b)Using your sample space in part (a), list the outcomes for each of the following events
A = the event that both customers pick candy
B = the event that both customers pick the same type of topping
C = the event that at least one customer picks a candy topping
A:
B:
C:
a)List all the events in the sample space.
b)Using your sample space in part (a), list the outcomes for each of the following events
A = the event that both customers pick candy
B = the event that both customers pick the same type of topping
C = the event that at least one customer picks a candy topping
A:
B:
C:

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
34
Some limitations of the classical approach to probability were discussed in the text. Identify and briefly discuss one of these.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
35
U.S. Postal Service standards call for overnight delivery within a zone of about 60 miles for any first-class letter deposited by the last posted collection time. Two-day delivery is promised within a 600-mile zone, and three-day delivery is promised for distances over 600 miles. An accounting firm conducted an independent audit by "seeding" the mail with letters and recording on-time delivery rates for these letters. Suppose that the results of the study were as follows:  Use the given information to estimate the probability of an on-time delivery in New York.
Use the given information to estimate the probability of an on-time delivery in New York.
A)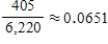
B)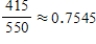
C)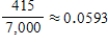
D)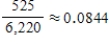
E)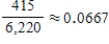
 Use the given information to estimate the probability of an on-time delivery in New York.
Use the given information to estimate the probability of an on-time delivery in New York.A)
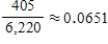
B)
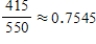
C)
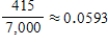
D)
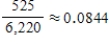
E)
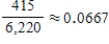

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
36
A small manufacturing firm has 250 employees. Fifty have been employed for less than 5 years and 125 have been with the company for over 10 years. Suppose that one employee is selected at random from a list of the employees. For the following events, compute the probabilities requested below.
A = the event the selected employee has been with the firm less than 5 years
B = the event the selected employee has been with the firm 5 ≤ x ≤ 10 years.
C = the event the selected employee has been with the firm over 10 years.
a)P(A)b)P(C)c)P(A or B)d)P(A and C)
A = the event the selected employee has been with the firm less than 5 years
B = the event the selected employee has been with the firm 5 ≤ x ≤ 10 years.
C = the event the selected employee has been with the firm over 10 years.
a)P(A)b)P(C)c)P(A or B)d)P(A and C)

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 5-1
In a survey of airline travelers, subjects were observed in the coach section of airplanes to determine if men or women are bothered by a seatmate of the opposite gender using the common armrest. ("Passengers who were asleep or lovers cuddled together were not counted, since these were considered confounding circumstances.")The table below contains data gathered in that study.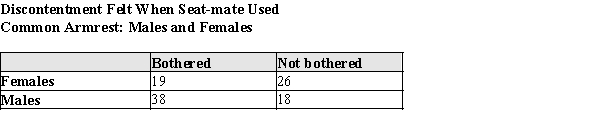 Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.
Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.
Refer to Exhibit 5-1.
a)What is the probability that the passenger is female?
b)What is the probability that the passenger is female or bothered?
c)What is the probability that the passenger is male and not bothered?
In a survey of airline travelers, subjects were observed in the coach section of airplanes to determine if men or women are bothered by a seatmate of the opposite gender using the common armrest. ("Passengers who were asleep or lovers cuddled together were not counted, since these were considered confounding circumstances.")The table below contains data gathered in that study.
 Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.
Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.Refer to Exhibit 5-1.
a)What is the probability that the passenger is female?
b)What is the probability that the passenger is female or bothered?
c)What is the probability that the passenger is male and not bothered?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
38
A small ferryboat transports vehicles from one island to another, and the order the vehicles arrive will lead to slightly different placement on the ferry. Consider the chance experiment where the type of vehicle--passenger (P) or recreational (R) vehicle--is recorded for each of the next two vehicles that arrive at the dock.
a)List all the events in the sample space.
b)Using your sample space in part (a), list the outcomes for each of the following events:
A = the event that both vehicles are passenger cars
B = the event that both vehicles are of the same type
C = the event that there is at least one passenger car
A:
B:
C:
a)List all the events in the sample space.
b)Using your sample space in part (a), list the outcomes for each of the following events:
A = the event that both vehicles are passenger cars
B = the event that both vehicles are of the same type
C = the event that there is at least one passenger car
A:
B:
C:

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the chance experiment in which a high school principal selects a sports event at random to attend. The sex of the participants (Male or Female) is noted, as well as the type of event (Wrestling, Volleyball, Basketball, or Swimming).
Let M be the event that the participants are male and B be the event that a ball is involved (i.e. basketball or volleyball).
a)What outcomes are in BC?
b)What outcomes are in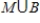 ?
?
c)What outcomes are in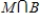 ?
?
Let M be the event that the participants are male and B be the event that a ball is involved (i.e. basketball or volleyball).
a)What outcomes are in BC?
b)What outcomes are in
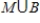 ?
?c)What outcomes are in
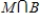 ?
?
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
40
In a few sentences, define the following terms:
a)Sample space
b)Mutually exclusive
a)Sample space
b)Mutually exclusive

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
41
At Thomas Jefferson High School students are heavily involved in extra-curricular activities. Suppose that a student is selected at random from the students at this school. Let the events A, M, and S be defined as follows, with probabilities listed: 
Calculate each of the following (show your work):
i)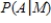 ii)
ii) 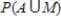 iii)
iii) 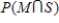

Calculate each of the following (show your work):
i)
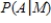 ii)
ii) 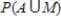 iii)
iii) 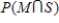

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
42
A man has five ties and each day chooses a tie at random to wear to work. He is colorblind and is wife frequently complains that he wears the same tie two days in a row. Your task is to design and conduct a simulation that could be used to estimate the probability that he wears the same tie two days in a row in a 5-day week.
a)To simulate the first strategy discussed above, assign digits to the ties that will result in the probability of selection of each tie to be the same.
Tie 1 Digits:
Tie 2 Digits:
Tie 3 Digits:
Tie 4 Digits:
Tie 5 Digits:
b)Describe how you would use a random digit table to conduct one run of your simulation.

a)To simulate the first strategy discussed above, assign digits to the ties that will result in the probability of selection of each tie to be the same.
Tie 1 Digits:
Tie 2 Digits:
Tie 3 Digits:
Tie 4 Digits:
Tie 5 Digits:
b)Describe how you would use a random digit table to conduct one run of your simulation.


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
43
In a special report, "Speed Demons," in the Cedar Rapids, IA, Gazette, reporters used a radar gun to check the speeds of motorists in two counties. They were shocked (!) to discover that some motorists were driving at a speed greater than the posted limits. They reported the following information: 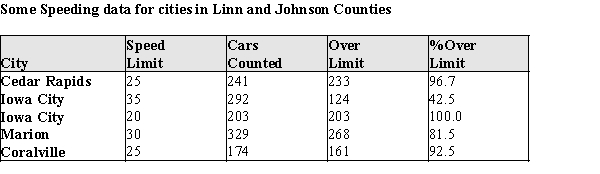 Suppose that one of these cars is selected at random. Consider the following events:
Suppose that one of these cars is selected at random. Consider the following events:
F = the event that a driver is in a "fast lane" (speed limit above 25 mph).
S = the event that a driver is speeding.

b)From the information in part (a), calculate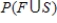 .
.
c)From the information in part (a), calculate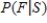 .
.
d)From the information in part (a), calculate P(S).
e)These events are represented in a tree diagram below. What is the probability that a randomly selected driver will "follow the branches" to the X?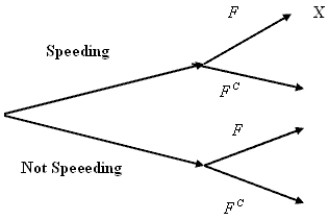
 Suppose that one of these cars is selected at random. Consider the following events:
Suppose that one of these cars is selected at random. Consider the following events:F = the event that a driver is in a "fast lane" (speed limit above 25 mph).
S = the event that a driver is speeding.

b)From the information in part (a), calculate
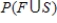 .
.c)From the information in part (a), calculate
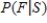 .
.d)From the information in part (a), calculate P(S).
e)These events are represented in a tree diagram below. What is the probability that a randomly selected driver will "follow the branches" to the X?


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
44
Consider the following two games:
Game 1: There are 10 balls of different colors, you pick one of the proposed balls. After you have made your choice and have put the ball back, one ball is selected at random. If the selected ball matches the ball you picked, you win.
Game 2: There are 6 balls of different colors, you pick two of the proposed balls. After you have made your choices and have put balls back, two different balls are selected at random. If the selected balls match the two you picked, you win.
If you can only play one of these games, which game would you pick to win and why? Use relevant probabilities to justify your choice.
A)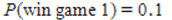 and
and 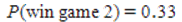 , therefore it is advantageous to play game 1 because the probability of winning is higher.
, therefore it is advantageous to play game 1 because the probability of winning is higher.
B)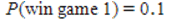 and
and 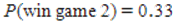 , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
C)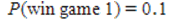 and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
D)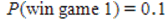 and
and 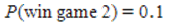 , therefore it is no matter what game to play because the probabilities of winning are equal.
, therefore it is no matter what game to play because the probabilities of winning are equal.
E)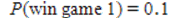 and
and 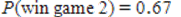 , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
Game 1: There are 10 balls of different colors, you pick one of the proposed balls. After you have made your choice and have put the ball back, one ball is selected at random. If the selected ball matches the ball you picked, you win.
Game 2: There are 6 balls of different colors, you pick two of the proposed balls. After you have made your choices and have put balls back, two different balls are selected at random. If the selected balls match the two you picked, you win.
If you can only play one of these games, which game would you pick to win and why? Use relevant probabilities to justify your choice.
A)
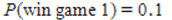 and
and 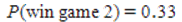 , therefore it is advantageous to play game 1 because the probability of winning is higher.
, therefore it is advantageous to play game 1 because the probability of winning is higher.B)
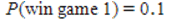 and
and 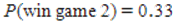 , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.C)
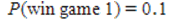 and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.D)
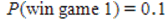 and
and 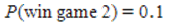 , therefore it is no matter what game to play because the probabilities of winning are equal.
, therefore it is no matter what game to play because the probabilities of winning are equal.E)
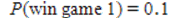 and
and 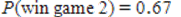 , therefore it is advantageous to play game 2 because the probability of winning is higher.
, therefore it is advantageous to play game 2 because the probability of winning is higher.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
45
In a particular city, 45% of donors have type O blood. On a certain day, the blood bank needed 4 donors with type O blood to restock their reserves. The director has the option of waiting to get 4 donors during the day, or ordering type O blood from a neighboring blood bank. The director would like to replace the blood before 12 donors come to the bank, the typical number to arrive before noon. Your task is to design and conduct a simulation to estimate the probability it takes 12 or more donors to get 4 with type O blood.
a)To simulate the arrival of blood donors from this population, assign digits to the blood types that will result in a probability of success (Type O donor) of 0.45.
Type O Digits:
Other than Type O Digits:
b)Describe how you would use a random digit table to conduct one run of your simulation.
c)Using the following lines from a random digit table, perform 5 runs. Based on your results, what do you estimate to be the probability of getting 4 Type O donors before 12 donors arrive at the blood bank? (Mark on the digits to help explain your procedure.)
a)To simulate the arrival of blood donors from this population, assign digits to the blood types that will result in a probability of success (Type O donor) of 0.45.
Type O Digits:
Other than Type O Digits:
b)Describe how you would use a random digit table to conduct one run of your simulation.
c)Using the following lines from a random digit table, perform 5 runs. Based on your results, what do you estimate to be the probability of getting 4 Type O donors before 12 donors arrive at the blood bank? (Mark on the digits to help explain your procedure.)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
46
Experimental studies utilize blinding to prevent researchers from biasing their measurements of the patients. But can they guess the treatment? In a study of a drug intervention, clinicians who were "blinded" were asked to guess what treatment their patients received. Data from that experiment are shown below. Assume that these data are indicative of the population of these treatments. 
a)If a subject is selected at random, what is the probability that the researcher correctly guesses the treatment?
b)If a randomly chosen subject received the standard treatment, what is the probability that the researcher correctly guesses the treatment?

a)If a subject is selected at random, what is the probability that the researcher correctly guesses the treatment?
b)If a randomly chosen subject received the standard treatment, what is the probability that the researcher correctly guesses the treatment?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
47
Three of the most common pets that people have are cats, dogs, and fish. In fact, many families have more than one type of pet, and some have all three! Suppose that a family is selected at random. Define the following events, with the probabilities given. (Note: the fish-and-cats combination doesn't seem too popular!) 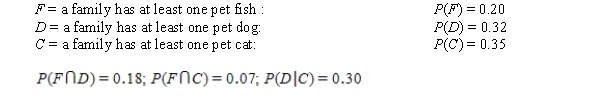
Calculate each of the following (show your work):
i)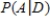 ii)
ii) 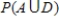 iii)
iii) 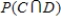
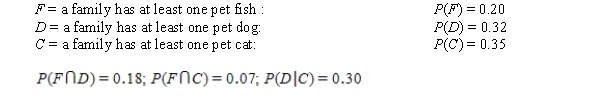
Calculate each of the following (show your work):
i)
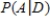 ii)
ii) 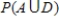 iii)
iii) 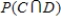

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
48
Exhibit 5-1
In a survey of airline travelers, subjects were observed in the coach section of airplanes to determine if men or women are bothered by a seatmate of the opposite gender using the common armrest. ("Passengers who were asleep or lovers cuddled together were not counted, since these were considered confounding circumstances.")The table below contains data gathered in that study. Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.
Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.
In the study in Exhibit 5-1, passengers were also classified by age: Suppose one of these passengers was randomly selected. Calculate the probability that:
Suppose one of these passengers was randomly selected. Calculate the probability that:
a)The passenger is under 40, given that she is female.
b)The passenger was bothered, given that the passenger was over 40.
c)The passenger was male and over 40.
In a survey of airline travelers, subjects were observed in the coach section of airplanes to determine if men or women are bothered by a seatmate of the opposite gender using the common armrest. ("Passengers who were asleep or lovers cuddled together were not counted, since these were considered confounding circumstances.")The table below contains data gathered in that study.
 Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.
Suppose one of these passengers was randomly selected. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation.In the study in Exhibit 5-1, passengers were also classified by age:
 Suppose one of these passengers was randomly selected. Calculate the probability that:
Suppose one of these passengers was randomly selected. Calculate the probability that:a)The passenger is under 40, given that she is female.
b)The passenger was bothered, given that the passenger was over 40.
c)The passenger was male and over 40.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose a survey was conducted among women ages 20 to 40. Consider the following events: 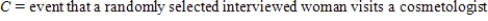
And
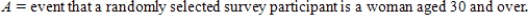
Data from the survey were used to estimate the following probabilities:
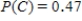
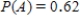
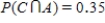
Use the given probability information to select a "hypothetical 1000" table.
A)
B)
C)
D)
E)
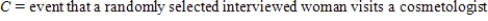
And
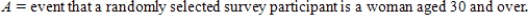
Data from the survey were used to estimate the following probabilities:
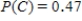
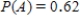
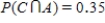
Use the given probability information to select a "hypothetical 1000" table.
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
50
In November 2002, Janet Napolitano, a Democrat, was elected Governor of Arizona, defeating Republican Matt Salmon and Independent Richard Mahoney. This was a somewhat surprising outcome, since there are more registered Republicans than Democrats in the state. The table below presents the results of a sample of voters in the election. The number who voted for each of the candidates is presented in the rows, and the party affiliation of the voters is presented in the columns. Suppose that a voter is randomly chosen from these respondents. Use the information in the table to answer the questions below. In showing your work, define and use appropriate notation. 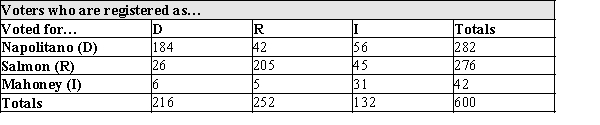
a)What is the probability that a randomly chosen voter voted for Napolitano?
b)What is the probability that a randomly chosen voter is a registered Democrat?
c)What is the probability that a randomly chosen voter cast a vote for Napolitano, given that the selected voter is a Democrat?
d)Commenting on this election. A local reporter said, "Napolitano won because she attracted a larger share of crossover voters." (A crossover voter is defined as one who votes differently than his or her party affiliation). What is the probability that a randomly chosen voter cast a vote for Napolitano, given that he or she is a crossover voter?

a)What is the probability that a randomly chosen voter voted for Napolitano?
b)What is the probability that a randomly chosen voter is a registered Democrat?
c)What is the probability that a randomly chosen voter cast a vote for Napolitano, given that the selected voter is a Democrat?
d)Commenting on this election. A local reporter said, "Napolitano won because she attracted a larger share of crossover voters." (A crossover voter is defined as one who votes differently than his or her party affiliation). What is the probability that a randomly chosen voter cast a vote for Napolitano, given that he or she is a crossover voter?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
51
An Australian snake, the diamond python, is about 3 feet long as an adult. In a study of the habitats of these creatures, micro transmitters were attached to their bodies and their locations were monitored. The following table displays the locations of these snakes by season of the year and habitat. The "other" category includes trees, logs, rocks, open ground, and under filtering cover (shrubs). 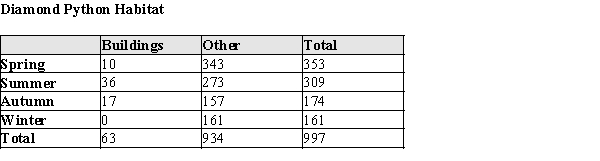 Suppose these habitat locations are representative of diamond python behavior in the different seasons. Calculate the estimated probability that:
Suppose these habitat locations are representative of diamond python behavior in the different seasons. Calculate the estimated probability that:
a)A randomly selected diamond back would be located in a building, given that it is spring.
b)A randomly selected diamond back would be located other than in a building given that it is spring or summer.
c)A randomly selected diamond back is observed in a building or in the summer.
 Suppose these habitat locations are representative of diamond python behavior in the different seasons. Calculate the estimated probability that:
Suppose these habitat locations are representative of diamond python behavior in the different seasons. Calculate the estimated probability that:a)A randomly selected diamond back would be located in a building, given that it is spring.
b)A randomly selected diamond back would be located other than in a building given that it is spring or summer.
c)A randomly selected diamond back is observed in a building or in the summer.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
52
Black bears (Ursus americanus) have a tendency to wander for food, and they have a high level of curiosity. These characteristics will sometimes get them into trouble when they travel through human-use areas such as parks. When they become "nuisances," the Park Service transplants them if possible to other areas. The outcomes of such transplants in Glacier National Park over a 10-year period are given in the table below: 
a)From these data, estimate the probability that a randomly selected transplanted bear would be male and a nuisance in another area.
b)From these data, estimate the probability that a randomly selected transplanted bear would be female or successfully transplanted.
c)From these data, estimate the probability that a randomly selected transplanted bear would return to the capture area if she is a female.
d)After combining the above data with other National Parks, officials estimated that only about 22% of black bears in all parks become enough of a nuisance to be transplanted. They further estimate that 84% of nuisance bears are male, and fifty percent of non-nuisance bears are females. If a randomly selected bear is observed to be a male, what is the probability it will be a nuisance?

a)From these data, estimate the probability that a randomly selected transplanted bear would be male and a nuisance in another area.
b)From these data, estimate the probability that a randomly selected transplanted bear would be female or successfully transplanted.
c)From these data, estimate the probability that a randomly selected transplanted bear would return to the capture area if she is a female.
d)After combining the above data with other National Parks, officials estimated that only about 22% of black bears in all parks become enough of a nuisance to be transplanted. They further estimate that 84% of nuisance bears are male, and fifty percent of non-nuisance bears are females. If a randomly selected bear is observed to be a male, what is the probability it will be a nuisance?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
53
One method for increasing sales of boxes of cereal is to suggest to children that they complete a "set" of small toys. Suppose one of a set of five toys is put in every box. Using one strategy the company could put a randomly selected toy in each box of cereal. Then each toy would appear in 20% of the boxes. You are to design a simulation that will assess this strategy and the likely number of boxes of cereal needed to complete the set of toys.
a)To simulate this strategy, assign digits to the toys that will result in the probability of selection of each toy to be 0.20.
Toy 1 Digits:
Toy 2 Digits:
Toy 3 Digits:
Toy 4 Digits:
Toy 5 Digits:
b)Describe how you would use a random digit table to conduct one run of your simulation, where one run continues until a complete set of the 5 toys is acquired.

d)Suppose that the cereal company decides to put the toys in the boxes with different probabilities. Toy 1 will be put in 30% of the boxes, Toys 2 and 3 will be put in 20% of the boxes, and Toys 4 and 5 will be put in 15% of the boxes. Assign digits to the toys that will simulate these probabilities.
Toy 1 Digits:
Toy 2 Digits:
Toy 3 Digits:
Toy 4 Digits:
Toy 5 Digits:

a)To simulate this strategy, assign digits to the toys that will result in the probability of selection of each toy to be 0.20.
Toy 1 Digits:
Toy 2 Digits:
Toy 3 Digits:
Toy 4 Digits:
Toy 5 Digits:
b)Describe how you would use a random digit table to conduct one run of your simulation, where one run continues until a complete set of the 5 toys is acquired.

d)Suppose that the cereal company decides to put the toys in the boxes with different probabilities. Toy 1 will be put in 30% of the boxes, Toys 2 and 3 will be put in 20% of the boxes, and Toys 4 and 5 will be put in 15% of the boxes. Assign digits to the toys that will simulate these probabilities.
Toy 1 Digits:
Toy 2 Digits:
Toy 3 Digits:
Toy 4 Digits:
Toy 5 Digits:


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
54
Some article reported the following approximate probabilities based on a survey of adults ages 18 to 40: 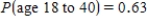
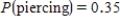
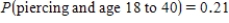 Use the given probability information to select a "hypothetical 1000" table.
Use the given probability information to select a "hypothetical 1000" table.
A)
B)
C)
D)
E)
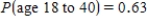
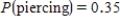
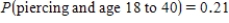 Use the given probability information to select a "hypothetical 1000" table.
Use the given probability information to select a "hypothetical 1000" table.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose there are two detectives in a small private office that is engaged in the search for people and the probability that a person will be found for each of the two detectives is equal to 0.754 for Detective 1 and 0.831 for Detective 2. Further, suppose that Detective 1 works part-time and considers 40% of cases of missing people and that Detective 2 considers the remaining 60%. Use the given probability information to select a "hypothetical 1000" table.
A)
B)
C)
D)
E)
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck


